Разграничение сред по признаку электропроводности

Приводятся критерии классификации электромагнитных полей. Рассматривается относительность разграничения сред по электропроводности.

Критериями классификации электромагнитных полей служит характер их зависимости от времени и величина тока проводимости. В связи с этим, принято различать следующие виды электромагнитных полей:

1. Статические поля

- характеризуются постоянством во времени, т.е. d/dt = 0

- отсутствием тока проводимости I_пр = 0

Положив эти значения в уравнения Максвелла, увидим, что система уравнений распадается на две полностью независимые системы:

а) Величины первой системы характеризуют электрическое поле:

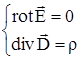                                                                 (1.34а)

б) Величины второй системы характеризуют магнитостатическое поле:                      

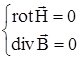                                                            (1.34б)

Таким образом, электростатические поля и магнитостатические поля можно рассматривать независимо друг от друга, в этом и заключается одна из их особенностей. Электростатическое поле порождается неподвижными электрическими зарядами, магнитостатическое поле порождается неподвижными постоянными магнитами.

2. Стационарные поля

- характеризуются постоянством во времени, т.е. d/dt = 0

- наличием тока проводимости

В этом случае уравнения Максвелла приводятся к виду:

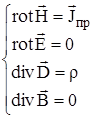                                                              (1.35)

Нетрудно заметить, что в стационарных полях уже существует связь между электрическими и магнитными полями, которая осуществляется через плотность тока проводимости (поскольку ).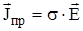

3. Квазистационарные поля

- характеризуются тем, что d/dt ¹ 0, однако плотность тока проводимости намного больше плотности тока смещения, т.е.:

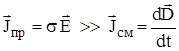
В этом случае уравнения Максвелла принимают вид:

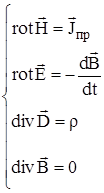                                                                    (1.36)

К квазистационарным полям относят электромагнитные явления, протекающие достаточно медленно. Рассмотрим пример. 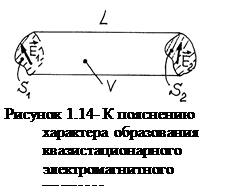 Пусть в некотором объеме V распро-страняется переменный электромагнитный процесс (см. рис.1.14). Предположим, что в некоторый момент времени t₁ в сечении S₁ существует некое электрическое поле характеризуемое как:

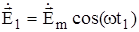
Очевидно, что на расстоянии L от S₁ (т.е. в сечении S₂) электрическое поле будет:

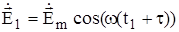
где: t - время прохождения электромагнитного процесса отрезка L, 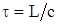,  с - скорость света. Чтобы  было равно , необходимо, чтобы wt = 0, или 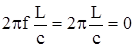, или l >> L, где:  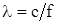– длина волны.

Вывод: Для рассматриваемого объема V можно говорить о почти постоянном (квазистационарном) характере электромагнитного поля только в том случае если выполняется условие:

                          l >> L                                                        (1.37)

Данное условие получило название условия квазистационарности. Следовательно, при любой скорости электромагнитного процесса система может быть квазистационарной, если ее размеры достаточно малы по отношению к длине волны.

4.Быстропеременные поля.

Это такие электромагнитные поля, которые полностью характеризуются системой уравнений Максвелла (1.28 или 1.29) без каких либо упрощений.

Перейдем теперь к рассмотрению вопроса о разграничении сред по признаку электропроводности. В разделе 1.3, в зависимости от значения принимаемой удельной проводимости s, среды разделялись на диэлектрики и проводники. Другой мерой оценки явления электропроводности может служить плотность полного тока:

.

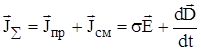Для идеального диэлектрика (s = 0): 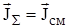, тогда как для идеального проводника (s = ¥): 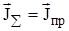. Следовательно, любую реальную среду можно считать диэлектриком если: .

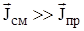     Если же 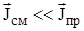, то такую среду можно считать проводником. Применим данный критерий к гармонически изменяющимся во времени полям. Для них: 

                                 .

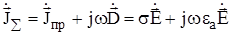Среда характеризуется как диэлектрик если:

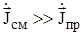,       или 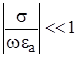          .                    (1.38 а)

Среда характеризуется как проводник если:

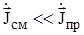,       или 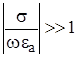          .                        (1.38 б)

Из (1.38) видно, что деление сред на проводники и диэлектрики по их электропроводимости относительно, т.к. критерий оценки включает в себя еще и частоту. Это означает, что одна и та же среда может вести себя как проводник на одних частотах, и как диэлектрик на других.

Частота на которой выполняется условие 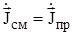  ( 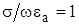) носит название граничной f_гр. Тогда, если рабочая частота f_раб >> f_гр, то среда считается диэлектриком. Если же f_раб << f_гр – то проводником.

Пример. Для пресной воды (см.табл.1.1): e = 80, s = 2 ^. 10^-3 см/м. Тогда из условия: 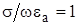, определяем f_гр = 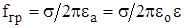, где:  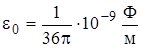- диэлектрическая проницаемость вакуума. Подставив значения в (1.38 а), получим: f_гр » 500 кГц.

Это означает, что:

- при f = 50 Гц – вода является проводником (хорошо известный из практики факт);

- при f = 1 ГГц – вода будет является диэлектриком.