Основные уравнения
Электромагнитного поля
Вся теория электромагнитного поля базируется на четырех экспериментально установленных законах. Это закон Ш.О.Кулона, теоремы К.Га-усса для электрической и магнитной индукции, закон М. Фарадея и закон полного тока А. Ампера. Эти законы были обобщены Дж. К. Максвеллом, который привлек к созданию своей теории великую гипотезу о токе смещения.
Уравнения Максвелла являются фундаментальными в том смысле, что пока не известны более общие законы природы, из которых бы они вытекали. Поэтому уравнения Максвелла нужно знать наизусть! Остальное не нужно заучивать, а нужно понять.
 |
1.1 Векторные характеристики электромагнитного поля
Обсуждаются основные понятия и величины, характеризующие электромагнитное поле в некоторой области пространства
 |

Действие электромагнитного поля обладает определенной направленностью, поэтому для его описания вводят векторные величины.
Рассмотрим векторные характеристики, при помощи которых определяется электромагнитное поле. Их четыре:
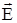 – вектор напряженности электрического поля;
– вектор напряженности электрического поля;
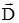 – вектор электрической индукции;
– вектор электрической индукции;
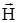 – вектор напряженности магнитного поля;
– вектор напряженности магнитного поля;
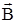 – вектор магнитной индукции.
– вектор магнитной индукции.
Определить поле в некоторой области пространства – значит указать эти векторы поля в любой её точке. Дадим теперь определения и рассмотрим физическую сущность векторов электромагнитного поля.
Вектор напряженности электрического поля 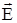 определяют как силу, с которой электрическое поле действует на внесенный точечный положительный единичный заряд. Связь между вектором
определяют как силу, с которой электрическое поле действует на внесенный точечный положительный единичный заряд. Связь между вектором 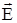 и силой
и силой 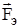 , действующей на точечный заряд q, определяется как:
, действующей на точечный заряд q, определяется как:
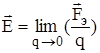 . (1.1)
. (1.1)
Следовательно, вектор 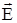 характеризует именно силовое воздействие электрического поля на заряженные частицы. По закону Кулона:
характеризует именно силовое воздействие электрического поля на заряженные частицы. По закону Кулона:
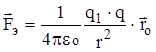 , где:
, где: 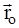 - единичный вектор.
- единичный вектор.
Отсюда:
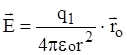 , [В/м] (1.2)
, [В/м] (1.2)
здесь: 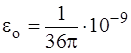 , [Ф/м] - диэлектрическая проницаемость вакуума.
, [Ф/м] - диэлектрическая проницаемость вакуума.
Если ограничится только исследованием процессов в вакууме, то задание напряженности электрического  поля в каждой точке пространства является достаточным. Однако, как будет показано далее, для правильного описания электрического поля в материальных средах, требуется ввести в рассмотрение второе векторное поле, характеризуемое вектором электрической индукции (электрического сме-щения)
поля в каждой точке пространства является достаточным. Однако, как будет показано далее, для правильного описания электрического поля в материальных средах, требуется ввести в рассмотрение второе векторное поле, характеризуемое вектором электрической индукции (электрического сме-щения) 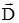 . Вектор
. Вектор 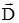 в вакууме связан с векто-ром
в вакууме связан с векто-ром 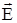 соотношением:
соотношением:
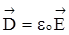 . (1.3)
. (1.3)
Если в формуле (1.2) вместо 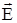 подставить вели-чину
подставить вели-чину 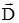 /eо, то закон Кулона примет вид:
/eо, то закон Кулона примет вид:
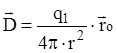 ; [Кл/м2] (1.4)
; [Кл/м2] (1.4)
В отличие от электрического поля, которое оказывает силовое воздействие на заряд, находящийся в покое или в движении, магнитное поле действует только на движущиеся заряды.
Вектор магнитной индукции 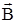 определяют как силу, с которой магнитное поле действует на движущийся положительный единичный заряд. Связь между вектором
определяют как силу, с которой магнитное поле действует на движущийся положительный единичный заряд. Связь между вектором 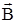 и силой
и силой 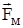 , действую-щей на точечный заряд q, определяется выражением:
, действую-щей на точечный заряд q, определяется выражением:
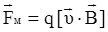 , (1.5)
, (1.5)
где: 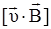 - векторное произведение векторов скорости движения заряда
- векторное произведение векторов скорости движения заряда 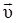 и вектора магнит-ной индукции
и вектора магнит-ной индукции 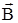 .
.
Из формулы (1.5) следует, что магнитная индукция численно равна силе, с которой магнитное поле действует на единичный точечный заряд, движущийся со скоростью 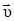 перпендикулярно линиям вектора
перпендикулярно линиям вектора 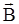 . Магнитная индукция измеряется в Веберах на квадратный метр (Вб/м2). Сила воздействия магнитного поля на движущийся заряд зависит от магнитных свойств среды. Поэтому, подобно тому как это было сделано для электрического поля, удобно ввести еще одну векторную величину для полного описания явлений, происходящих в материальных средах, помещенных в магнитное поле. Это второе векторное поле характеризуется
. Магнитная индукция измеряется в Веберах на квадратный метр (Вб/м2). Сила воздействия магнитного поля на движущийся заряд зависит от магнитных свойств среды. Поэтому, подобно тому как это было сделано для электрического поля, удобно ввести еще одну векторную величину для полного описания явлений, происходящих в материальных средах, помещенных в магнитное поле. Это второе векторное поле характеризуется  напряженностью магнитного поля
напряженностью магнитного поля 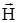 и в вакууме связано с
и в вакууме связано с 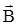 соотношением
соотношением
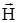 =
= 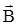 /mо ,
/mо ,
откуда: 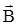 = mо
= mо 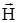 . (1.6)
. (1.6)
Напряженность магнитного поля 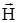 имеет размер-ность “Ампер на метр” (А/м). Величина mо = 4p×10-7 называется магнитной проницаемостью вакуума и имеет размерность “Генри на метр” (Гн/м).
имеет размер-ность “Ампер на метр” (А/м). Величина mо = 4p×10-7 называется магнитной проницаемостью вакуума и имеет размерность “Генри на метр” (Гн/м).
Для электрического заряда, двигающегося одновременно в электрическом и магнитном полях, мы можем написать уравнения движения уже с учетом всех действующих сил:
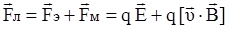 .
.
Сила 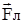 носит название силы Лоренца.
носит название силы Лоренца.
Величину и направление напряженности элек-трического магнитного полей в пространстве удобно изображать при помощи силовых линий, как показано на рис.1.1. Силовой линией назы-вается такая линия, касательная к которой в каждой точке совпадает с вектором напря-женности в этой же точке. Густота силовых линий условно характеризует модуль амплитуды напряженности поля. Направление напряженности указывается стрелкой.
 |
1.2 Электромагнитные параметры среды
Рассматривается характер влияния электрического и магнитного полей на материальные среды и параметры, количественно характеризующие это влияние.
 |
 Уравнения (1.3) и (1.6) характеризуют связь между векторами электромагнитного поля в вакууме. Для установления связи между этими векторами в некоторой материальной среде, необходимо рассмотреть явления, возникающие в материальных средах при воздействии на них электрического и магнитного поля.
Уравнения (1.3) и (1.6) характеризуют связь между векторами электромагнитного поля в вакууме. Для установления связи между этими векторами в некоторой материальной среде, необходимо рассмотреть явления, возникающие в материальных средах при воздействии на них электрического и магнитного поля.
Рассмотрим сначала воздействие электрического поля. 
 При отсутствии внешнего электрического поля молекула материальной сред
При отсутствии внешнего электрического поля молекула материальной сред 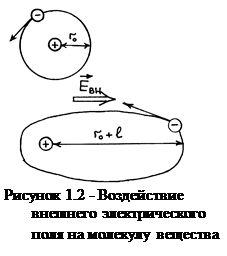 (например, молекула водорода) представляется в виде положи-тельного ядра в центре и вращающегося вокруг него электрона (см. рис.1.2). Посколь-ку орбита вращения практически круговая, то можно считать, что молекула электри-чески нейтральна. При приложении внеш-него электрического поля орбита электрона деформируется, центры положительного и отрицательного, зарядов не совпадают в пространстве. В результате молекула начинает вести себя подобно электрическому диполю, т.е. системе двух связанных противоположно заряженных частиц:
(например, молекула водорода) представляется в виде положи-тельного ядра в центре и вращающегося вокруг него электрона (см. рис.1.2). Посколь-ку орбита вращения практически круговая, то можно считать, что молекула электри-чески нейтральна. При приложении внеш-него электрического поля орбита электрона деформируется, центры положительного и отрицательного, зарядов не совпадают в пространстве. В результате молекула начинает вести себя подобно электрическому диполю, т.е. системе двух связанных противоположно заряженных частиц:
 |
 Описанное явление носит название электронной поляризации вещества. Таким образом, при приложении внешнего электрического поля, все молекулы, образовав электрические диполи, займут определенную ориентацию относительно приложенного поля. Внутри материальной среды возникает специфический вид объемного электрического заряда, носящего название поляризационный заряд.
Описанное явление носит название электронной поляризации вещества. Таким образом, при приложении внешнего электрического поля, все молекулы, образовав электрические диполи, займут определенную ориентацию относительно приложенного поля. Внутри материальной среды возникает специфический вид объемного электрического заряда, носящего название поляризационный заряд.
Количественной характеристикой поляризации отдельной молекулы служит ее дипольный момент:
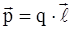 ,
,
где: q – электрический заряд молекулы;
l – смещение электрического заряда молекулы.
Если в единице объема DV находится N молекулярных диполей, то в качестве меры поляризации диэлектрика вводят вектор поляризации.
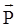 =
= 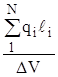 .
.
Для подавляющего большинства веществ существует прямая зависимость между векторами 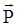 и
и 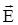 :
:
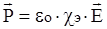 ,
,
где: e0 – диэлектрическая постоянная вакуума, cэ- называется электрической восприимчивостью вещества. Для вакуума, где вещество отсутствует, cэ = 0.
На основании изложенного определим вектор электрической индукции 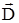 в материальной среде как сумму вектора поляризации и вектора
в материальной среде как сумму вектора поляризации и вектора 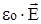 , т.е.:
, т.е.:
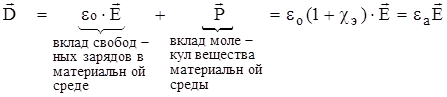 , (1.7)
, (1.7)
где: eа = e0 (1 + cэ) = e0 e – абсолютная диэлектрическая проницаемость среды;
e = 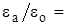 (1 + cэ) – относительная диэлектрическая проницаемость среды.
(1 + cэ) – относительная диэлектрическая проницаемость среды.
Из (1.7) видно, что вектор 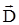 не является чисто полевым вектором, поскольку учитывает поляризованность среды, т.е. "реакцию" материальной среды на воздействие электрического поля.
не является чисто полевым вектором, поскольку учитывает поляризованность среды, т.е. "реакцию" материальной среды на воздействие электрического поля.
Рассмотрим теперь воздействие магнитного поля на материальную среду.
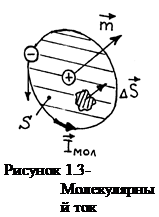 При отсутствии внешнего магнитного поля, согласно классическим представлениям, молекулы матери-альной среды несут в себе замкнутые токи (так называемая гипотеза Ампера). Обозначим через Iмол величину молекулярного тока, через D
При отсутствии внешнего магнитного поля, согласно классическим представлениям, молекулы матери-альной среды несут в себе замкнутые токи (так называемая гипотеза Ампера). Обозначим через Iмол величину молекулярного тока, через D 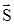 – площадь элементарной площадки, вдоль границы которой течет Iмол (рис.1.3). Тогда для количественной харак-теристики каждого отдельного молекулярного тока вводится понятие вектора магнитного момента молекулы:
– площадь элементарной площадки, вдоль границы которой течет Iмол (рис.1.3). Тогда для количественной харак-теристики каждого отдельного молекулярного тока вводится понятие вектора магнитного момента молекулы:
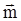 = Iмол D
= Iмол D 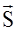 .
.
При приложении внешнего магнитного поля магнитные моменты молекул вещества частично ориентируются относительно внешнего поля. Таким образом, под воздействием внешнего магнитного поля материальная среда (вещество) приобретает определенную намагниченность.
Если в единице объема DV находится N молекулярных токов, то в качестве меры намагниченности вещества вводят понятие вектора намагниченности:
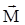 =
= 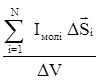 .
.
Для подавляющего большинства веществ существует прямая зависимость между векторами 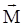 и
и 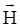 :
:
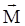 = m0×cм ×
= m0×cм × 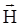 ,
,
где: m0 – магнитная постоянная вакуума; cм – магнитная восприимчивость среды. Для вакуума, где вещество отсутствует, cм = 0.
На основании изложенного определим вектор магнитной индукции 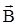 в материальной среде как сумму вектора намагниченности
в материальной среде как сумму вектора намагниченности 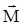 и вектора
и вектора 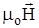 :
:
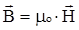 +
+ 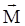 = mо (1 + cм)×
= mо (1 + cм)× 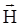 = mа
= mа 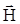 , (1.8)
, (1.8)
|
| ||||
где: mа = m0 (1 + cм) = m0×m – абсолютная магнитная проницаемость среды;
m = 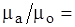 (1 + cм) – относительная магнитная проницаемость среды.
(1 + cм) – относительная магнитная проницаемость среды.
Несмотря на схожесть формы записи (1.8) с (1.7), в качестве характеристики, учитывающей "реакцию" материальной среды на воздействие магнитного поля, служит вектор напряженности магнитного поля 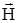 . Отсюда становится ясен физический смысл вектора
. Отсюда становится ясен физический смысл вектора 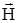 : он характеризует изменение магнитного поля в веществе, вызванное собственной намагниченностью среды при воздействии внешнего магнитного поля.
: он характеризует изменение магнитного поля в веществе, вызванное собственной намагниченностью среды при воздействии внешнего магнитного поля.
Кроме того, материальные среды обладают электропроводностью, т.е. в них под воздействием электрического поля возникает электрический ток, называемый током проводимости (т.е. упорядоченное движение носителей заряда). Закон, связывающий силу тока, протекающего по проводнику, с разностью потенциалов, приложенной к его концам, определяется законом Г.С. Ома: I = U/R. Если данное выражение записать для плотности тока проводимости, то получим закон Ома в дифференциальной форме. Следует четко разделять понятия плотность тока проводимости и ток проводимости. Если в некотором объеме DV происходит движение заряда с некоторой скоростью u, то в результате осуществляется перенос заряда в направлении скорости. Интенсивность этого переноса и характеризуется плотностью тока проводимости Jпр, определяемой формулой:
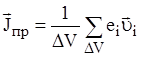 ,
,
где ui - скорость носителей заряда еi. Из этого выражения видно, что величина 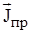 имеет размерность "А/м2" и в этом смысле действительно является мерой тока, протекающего через единичную площадку, перпендикулярную вектору скорости носителей заряда. Током проводимости называют отношение заряда, пересекающего конечную поверхность S, ко времени:
имеет размерность "А/м2" и в этом смысле действительно является мерой тока, протекающего через единичную площадку, перпендикулярную вектору скорости носителей заряда. Током проводимости называют отношение заряда, пересекающего конечную поверхность S, ко времени:
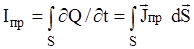 (1.9)
(1.9)
Перейдем теперь от обычной формы закона Ома к дифференциальной форме, для этого выделим внутри проводника с током весьма малых размеров цилиндр, торцы которого перпендикулярны линиям тока (рис.1.4).
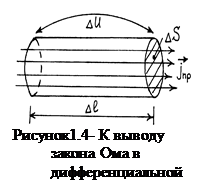 Из-за малости размеров цилиндра будем считать, что плотность тока проводимости постоянна в пределах его торцов, а линии тока параллельны его оси. Согласно закону Ома:
Из-за малости размеров цилиндра будем считать, что плотность тока проводимости постоянна в пределах его торцов, а линии тока параллельны его оси. Согласно закону Ома:
DIпр = DU / R , (1.10)
где: R - сопротивление цилиндра;
DU - напряжение между его торцами, которое равняется: DU = E×Dl.
Выразим сопротивление через удельную проводимость s:
R = Dl / (s×DS), (1.11)
далее подставим (1.10) в (1.9):
DIпр = s×E×DS.
Разделив обе части последнего равенства на DS, получим соотношение: Jпр = s E, которое можно переписать в векторной форме как:
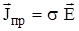 , (1.12)
, (1.12)
где: σ – удельная проводимость среды, которая учитывает силы “внутреннего трения” (столкновения с кристаллической решеткой) носителей тока при движении внутри вещества.
Уравнение (1.12) принято называть законом Ома в дифференциальной форме.
 |
Среда -
называется неоднородной, если εа, μа, и σ меняются от точки к точке и могут быть представлены как функции от пространственных координат.
В зависимости от значения удельной проводимости σ материальные среды подразделяют на три класса:
· диэлектрики, если σ £ 10 –5 См/м;
· проводники, если σ ³ 10 3 См/м;
· полупроводники, если 10 –5 < σ < 10 3 См/м.
Во многих задачах электродинамики реальный проводник или диэлектрик с успехом можно заменить на идеализированный. В этом случае используются понятия:
- идеальный проводник, σ = ∞;
- идеальный диэлектрик, σ = 0.
В качестве примера, ниже приведена таблица значений удельной проводимости (табл.1.1.) для некоторых материальных сред.
Таблица 1.1 –Удельные проводимости некоторых веществ
| Проводники | Диэлектрики | Полупроводники | |||
| Материал | σ, См/м | Материал | σ, См/м | Материал | σ, См/м |
| Серебро Медь Алюминий Железо Свинец | 6,14×107 5,65×107 3,54×107 1,0×107 0,48×107 | Кварц Мрамор Слюда Стекло Дерево | 2×10-17 ~ 10-8 ~ 10-13 ~ 10-12 ~ 10-9 | Земля сухая Земля влажная Вода пресная Вода морская | ~ 10-3 ~ 10-2.5 ~ 2×10-4 ~ 3¸5 |
 |
Максвелла
Формулируются теоремы Гаусса для электрической и магнитной индукции и характер обобщения этих теорем, сделанных Максвеллом. Дается физическая трактовка непрерывности магнитных силовых линий.
 |
 В электростатике известна теорема Гаусса, полученная на основе экспериментальных данных и устанавливающая связь между вектором электрической индукции
В электростатике известна теорема Гаусса, полученная на основе экспериментальных данных и устанавливающая связь между вектором электрической индукции 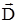 и величиной порождающего его электрического заряда q.
и величиной порождающего его электрического заряда q.
Теорема Гаусса для электрической индукции :
 Поток вектора электрической индукции
Поток вектора электрической индукции 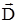 через любую замкнутую поверхность S равен электрическому заряду, заключенному внут-ри этой поверхности.
через любую замкнутую поверхность S равен электрическому заряду, заключенному внут-ри этой поверхности.
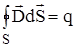 . (1.21)
. (1.21)
Данное выражение устанавливает:
- источниками силовых линий электрического поля могут являться только электрические заряды.
- силовые линии вектора электрической индукции выходят (начинаются) на положительном заряде и входят (заканчиваются) на отрицательном заряде. Т.е. силовые линии вектора 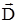 имеют исток и сток.
имеют исток и сток.
Количественно поток вектора электрической индукции через некоторую замкнутую поверхность S можно оценить числом пересекающих эту поверхность силовых линий. Причем:
- если число входящих линий больше выходящих, то поток считается отрицательным;
- если число входящих линий меньше выходящих, то поток считается положительным.
Поясним сказанное рис.1.11. Для соответствующих объемов V1, V2 и V3 имеем:
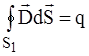 ;
; 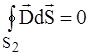 ;
; 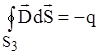 .
.
Максвелл обобщил теорему Гаусса, предложив рассматривать ее не только для постоянных полей, но и для переменных полей.
Представим (1.21) в более общем виде. Если в некотором замкнутом объеме V, ограниченном поверхностью S заключено несколько электрических зарядов, то совокупный заряд в этой области представляется через объемную плотность электрического заряда ρ:
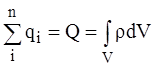 .
.
Тогда:
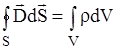 . (1.22)
. (1.22)
Полученное выражение носит название 3-го уравнения Максвелла : в интегральной форме:
 Поток вектора электрической индукции через любую замкнутую поверхность S равна сумме зарядов в объеме V , ограниченном этой поверхностью.
Поток вектора электрической индукции через любую замкнутую поверхность S равна сумме зарядов в объеме V , ограниченном этой поверхностью.
Для того, чтобы записать 3-е уравнение Максвелла в дифференциальной форме используем теорему Остроградского-Гаусса.
Тогда:
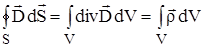 ,
,
или
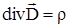 . (1.23)
. (1.23)
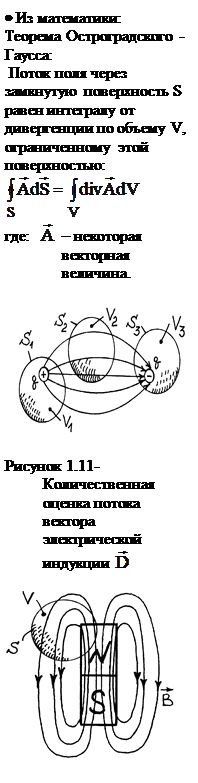 Уравнение (1.23) носит название 3-го уравнения Максвелла в дифференциальной форме.
Уравнение (1.23) носит название 3-го уравнения Максвелла в дифференциальной форме.
Из курса общей физики Вам известен экспериментальный факт, что силовые линии магнитного поля независимо от того, создано ли это поле постоянным магнитом или катушкой с переменным током, образуют в пространстве замкнутые линии (например, опыт с железными опилками и постоянным магнитом из школьной программы по физике).
Расположим внутри области существо-вания магнитного поля произвольный объем V, ограниченный поверхностью S. Из замкнутости силовых линий следует, что число входящих линий всегда будет равно числу входящих. Следовательно поток вектора магнитной индукции будет равен нулю. Этот факт закреплен в теореме Гаусса для магнитной индукции :
 Поток вектора магнитной индукции В через любую замкнутую поверхность S равен нулю:
Поток вектора магнитной индукции В через любую замкнутую поверхность S равен нулю:
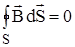 . (1.24)
. (1.24)
Уравнение (1.24) устанавливает:
- силовые линии вектора магнитной индукции всегда непрерывны, т.е. образуют замкнутые линии.
- в природе не существует магнитных зарядов.
Уравнение (1.24) кроме того, носит название 4-го уравнения Максвелла в интегральной форме.
Используя теорему Остроградского-Гаусса представим 4-ое уравнение Максвелла в дифференциальной форме:
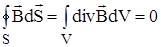 ,
,
Или:
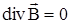 (1.25)
(1.25)
 |
Основные уравнения
Электромагнитного поля
Вся теория электромагнитного поля базируется на четырех экспериментально установленных законах. Это закон Ш.О.Кулона, теоремы К.Га-усса для электрической и магнитной индукции, закон М. Фарадея и закон полного тока А. Ампера. Эти законы были обобщены Дж. К. Максвеллом, который привлек к созданию своей теории великую гипотезу о токе смещения.
Уравнения Максвелла являются фундаментальными в том смысле, что пока не известны более общие законы природы, из которых бы они вытекали. Поэтому уравнения Максвелла нужно знать наизусть! Остальное не нужно заучивать, а нужно понять.
 |
1.1 Векторные характеристики электромагнитного поля
Обсуждаются основные понятия и величины, характеризующие электромагнитное поле в некоторой области пространства
 |

Действие электромагнитного поля обладает определенной направленностью, поэтому для его описания вводят векторные величины.
Рассмотрим векторные характеристики, при помощи которых определяется электромагнитное поле. Их четыре:
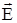 – вектор напряженности электрического поля;
– вектор напряженности электрического поля;
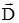 – вектор электрической индукции;
– вектор электрической индукции;
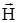 – вектор напряженности магнитного поля;
– вектор напряженности магнитного поля;
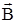 – вектор магнитной индукции.
– вектор магнитной индукции.
Определить поле в некоторой области пространства – значит указать эти векторы поля в любой её точке. Дадим теперь определения и рассмотрим физическую сущность векторов электромагнитного поля.
Вектор напряженности электрического поля 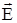 определяют как силу, с которой электрическое поле действует на внесенный точечный положительный единичный заряд. Связь между вектором
определяют как силу, с которой электрическое поле действует на внесенный точечный положительный единичный заряд. Связь между вектором 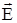 и силой
и силой 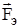 , действующей на точечный заряд q, определяется как:
, действующей на точечный заряд q, определяется как:
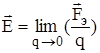 . (1.1)
. (1.1)
Следовательно, вектор 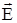 характеризует именно силовое воздействие электрического поля на заряженные частицы. По закону Кулона:
характеризует именно силовое воздействие электрического поля на заряженные частицы. По закону Кулона:
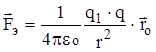 , где:
, где: 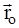 - единичный вектор.
- единичный вектор.
Отсюда:
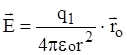 , [В/м] (1.2)
, [В/м] (1.2)
здесь: 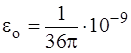 , [Ф/м] - диэлектрическая проницаемость вакуума.
, [Ф/м] - диэлектрическая проницаемость вакуума.
Если ограничится только исследованием процессов в вакууме, то задание напряженности электрического  поля в каждой точке пространства является достаточным. Однако, как будет показано далее, для правильного описания электрического поля в материальных средах, требуется ввести в рассмотрение второе векторное поле, характеризуемое вектором электрической индукции (электрического сме-щения)
поля в каждой точке пространства является достаточным. Однако, как будет показано далее, для правильного описания электрического поля в материальных средах, требуется ввести в рассмотрение второе векторное поле, характеризуемое вектором электрической индукции (электрического сме-щения) 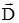 . Вектор
. Вектор 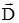 в вакууме связан с векто-ром
в вакууме связан с векто-ром 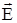 соотношением:
соотношением:
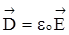 . (1.3)
. (1.3)
Если в формуле (1.2) вместо 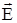 подставить вели-чину
подставить вели-чину 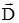 /eо, то закон Кулона примет вид:
/eо, то закон Кулона примет вид:
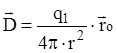 ; [Кл/м2] (1.4)
; [Кл/м2] (1.4)
В отличие от электрического поля, которое оказывает силовое воздействие на заряд, находящийся в покое или в движении, магнитное поле действует только на движущиеся заряды.
Вектор магнитной индукции 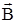 определяют как силу, с которой магнитное поле действует на движущийся положительный единичный заряд. Связь между вектором
определяют как силу, с которой магнитное поле действует на движущийся положительный единичный заряд. Связь между вектором 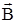 и силой
и силой 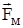 , действую-щей на точечный заряд q, определяется выражением:
, действую-щей на точечный заряд q, определяется выражением:
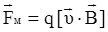 , (1.5)
, (1.5)
где: 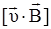 - векторное произведение векторов скорости движения заряда
- векторное произведение векторов скорости движения заряда 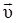 и вектора магнит-ной индукции
и вектора магнит-ной индукции 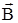 .
.
Из формулы (1.5) следует, что магнитная индукция численно равна силе, с которой магнитное поле действует на единичный точечный заряд, движущийся со скоростью 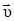 перпендикулярно линиям вектора
перпендикулярно линиям вектора 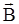 . Магнитная индукция измеряется в Веберах на квадратный метр (Вб/м2). Сила воздействия магнитного поля на движущийся заряд зависит от магнитных свойств среды. Поэтому, подобно тому как это было сделано для электрического поля, удобно ввести еще одну векторную величину для полного описания явлений, происходящих в материальных средах, помещенных в магнитное поле. Это второе векторное поле характеризуется
. Магнитная индукция измеряется в Веберах на квадратный метр (Вб/м2). Сила воздействия магнитного поля на движущийся заряд зависит от магнитных свойств среды. Поэтому, подобно тому как это было сделано для электрического поля, удобно ввести еще одну векторную величину для полного описания явлений, происходящих в материальных средах, помещенных в магнитное поле. Это второе векторное поле характеризуется  напряженностью магнитного поля
напряженностью магнитного поля 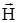 и в вакууме связано с
и в вакууме связано с 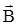 соотношением
соотношением
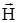 =
= 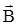 /mо ,
/mо ,
откуда: 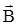 = mо
= mо 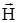 . (1.6)
. (1.6)
Напряженность магнитного поля 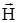 имеет размер-ность “Ампер на метр” (А/м). Величина mо = 4p×10-7 называется магнитной проницаемостью вакуума и имеет размерность “Генри на метр” (Гн/м).
имеет размер-ность “Ампер на метр” (А/м). Величина mо = 4p×10-7 называется магнитной проницаемостью вакуума и имеет размерность “Генри на метр” (Гн/м).
Для электрического заряда, двигающегося одновременно в электрическом и магнитном полях, мы можем написать уравнения движения уже с учетом всех действующих сил:
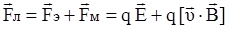 .
.
Сила 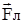 носит название силы Лоренца.
носит название силы Лоренца.
Величину и направление напряженности элек-трического магнитного полей в пространстве удобно изображать при помощи силовых линий, как показано на рис.1.1. Силовой линией назы-вается такая линия, касательная к которой в каждой точке совпадает с вектором напря-женности в этой же точке. Густота силовых линий условно характеризует модуль амплитуды напряженности поля. Направление напряженности указывается стрелкой.
 |
1.2 Электромагнитные параметры среды
Рассматривается характер влияния электрического и магнитного полей на материальные среды и параметры, количественно характеризующие это влияние.
 |
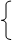 Уравнения (1.3) и (1.6) характеризуют связь между векторами электромагнитного поля в вакууме. Для установления связи между этими векторами в некоторой материальной среде, необходимо рассмотреть явления, возникающие в материальных средах при воздействии на них электрического и магнитного поля.
Уравнения (1.3) и (1.6) характеризуют связь между векторами электромагнитного поля в вакууме. Для установления связи между этими векторами в некоторой материальной среде, необходимо рассмотреть явления, возникающие в материальных средах при воздействии на них электрического и магнитного поля.
Рассмотрим сначала воздействие электрического поля. 
 При отсутствии внешнего электрического поля молекула материальной сред
При отсутствии внешнего электрического поля молекула материальной сред  (например, молекула водорода) представляется в виде положи-тельного ядра в центре и вращающегося вокруг него электрона (см. рис.1.2). Посколь-ку орбита вращения практически круговая, то можно считать, что молекула электри-чески нейтральна. При приложении внеш-него электрического поля орбита электрона деформируется, центры положительного и отрицательного, зарядов не совпадают в пространстве. В результате молекула начинает вести себя подобно электрическому диполю, т.е. системе двух связанных противоположно заряженных частиц:
(например, молекула водорода) представляется в виде положи-тельного ядра в центре и вращающегося вокруг него электрона (см. рис.1.2). Посколь-ку орбита вращения практически круговая, то можно считать, что молекула электри-чески нейтральна. При приложении внеш-него электрического поля орбита электрона деформируется, центры положительного и отрицательного, зарядов не совпадают в пространстве. В результате молекула начинает вести себя подобно электрическому диполю, т.е. системе двух связанных противоположно заряженных частиц:
 |
 Описанное явление носит название электронной поляризации вещества. Таким образом, при приложении внешнего электрического поля, все молекулы, образовав электрические диполи, займут определенную ориентацию относительно приложенного поля. Внутри материальной среды возникает специфический вид объемного электрического заряда, носящего название поляризационный заряд.
Описанное явление носит название электронной поляризации вещества. Таким образом, при приложении внешнего электрического поля, все молекулы, образовав электрические диполи, займут определенную ориентацию относительно приложенного поля. Внутри материальной среды возникает специфический вид объемного электрического заряда, носящего название поляризационный заряд.
Количественной характеристикой поляризации отдельной молекулы служит ее дипольный момент:
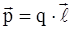 ,
,
где: q – электрический заряд молекулы;
l – смещение электрического заряда молекулы.
Если в единице объема DV находится N молекулярных диполей, то в качестве меры поляризации диэлектрика вводят вектор поляризации.
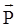 =
= 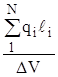 .
.
Для подавляющего большинства веществ существует прямая зависимость между векторами 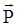 и
и 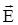 :
:
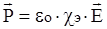 ,
,
где: e0 – диэлектрическая постоянная вакуума, cэ- называется электрической восприимчивостью вещества. Для вакуума, где вещество отсутствует, cэ = 0.
На основании изложенного определим вектор электрической индукции 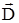 в материальной среде как сумму вектора поляризации и вектора
в материальной среде как сумму вектора поляризации и вектора 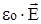 , т.е.:
, т.е.:
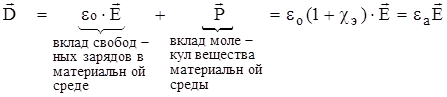 , (1.7)
, (1.7)
где: eа = e0 (1 + cэ) = e0 e – абсолютная диэлектрическая проницаемость среды;
e = 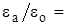 (1 + cэ) – относительная диэлектрическая проницаемость среды.
(1 + cэ) – относительная диэлектрическая проницаемость среды.
Из (1.7) видно, что вектор 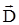 не является чисто полевым вектором, поскольку учитывает поляризованность среды, т.е. "реакцию" материальной среды на воздействие электрического поля.
не является чисто полевым вектором, поскольку учитывает поляризованность среды, т.е. "реакцию" материальной среды на воздействие электрического поля.
Рассмотрим теперь воздействие магнитного поля на материальную среду.
 При отсутствии внешнего магнитного поля, согласно классическим представлениям, молекулы матери-альной среды несут в себе замкнутые токи (так называемая гипотеза Ампера). Обозначим через Iмол величину молекулярного тока, через D
При отсутствии внешнего магнитного поля, согласно классическим представлениям, молекулы матери-альной среды несут в себе замкнутые токи (так называемая гипотеза Ампера). Обозначим через Iмол величину молекулярного тока, через D 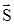 – площадь элементарной площадки, вдоль границы которой течет Iмол (рис.1.3). Тогда для количественной харак-теристики каждого отдельного молекулярного тока вводится понятие вектора магнитного момента молекулы:
– площадь элементарной площадки, вдоль границы которой течет Iмол (рис.1.3). Тогда для количественной харак-теристики каждого отдельного молекулярного тока вводится понятие вектора магнитного момента молекулы:
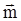 = Iмол D
= Iмол D 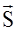 .
.
При приложении внешнего магнитного поля магнитные моменты молекул вещества частично ориентируются относительно внешнего поля. Таким образом, под воздействием внешнего магнитного поля материальная среда (вещество) приобретает определенную намагниченность.
Если в единице объема DV находится N молекулярных токов, то в качестве меры намагниченности вещества вводят понятие вектора намагниченности:
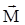 =
= 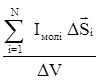 .
.
Для подавляющего большинства веществ существует прямая зависимость между векторами 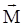 и
и 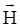 :
:
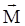 = m0×cм ×
= m0×cм × 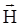 ,
,
где: m0 – магнитная постоянная вакуума; cм – магнитная восприимчивость среды. Для вакуума, где вещество отсутствует, cм = 0.
На основании изложенного определим вектор магнитной индукции 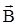 в материальной среде как сумму вектора намагниченности
в материальной среде как сумму вектора намагниченности 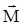 и вектора
и вектора 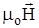 :
:
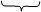
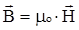 +
+ 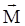 = mо (1 + cм)×
= mо (1 + cм)× 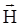 = mа
= mа 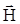 , (1.8)
, (1.8)
|
| ||||
где: mа = m0 (1 + cм) = m0×m – абсолютная магнитная проницаемость среды;
m = 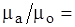 (1 + cм) – относительная магнитная проницаемость среды.
(1 + cм) – относительная магнитная проницаемость среды.
Несмотря на схожесть формы записи (1.8) с (1.7), в качестве характеристики, учитывающей "реакцию" материальной среды на воздействие магнитного поля, служит вектор напряженности магнитного поля 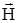 . Отсюда становится ясен физический смысл вектора
. Отсюда становится ясен физический смысл вектора 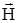 : он характеризует изменение магнитного поля в веществе, вызванное собственной намагниченностью среды при воздействии внешнего магнитного поля.
: он характеризует изменение магнитного поля в веществе, вызванное собственной намагниченностью среды при воздействии внешнего магнитного поля.
Кроме того, материальные среды обладают электропроводностью, т.е. в них под воздействием электрического поля возникает электрический ток, называемый током проводимости (т.е. упорядоченное движение носителей заряда). Закон, связывающий силу тока, протекающего по проводнику, с разностью потенциалов, приложенной к его концам, определяется законом Г.С. Ома: I = U/R. Если данное выражение записать для плотности тока проводимости, то получим закон Ома в дифференциальной форме. Следует четко разделять понятия плотность тока проводимости и ток проводимости. Если в некотором объеме DV происходит движение заряда с некоторой скоростью u, то в результате осуществляется перенос заряда в направлении скорости. Интенсивность этого переноса и характеризуется плотностью тока проводимости Jпр, определяемой формулой:
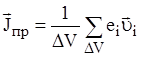 ,
,
где ui - скорость носителей заряда еi. Из этого выражения видно, что величина 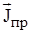 имеет размерность "А/м2" и в этом смысле действительно является мерой тока, протекающего через единичную площадку, перпендикулярную вектору скорости носителей заряда. Током проводимости называют отношение заряда, пересекающего конечную поверхность S, ко времени:
имеет размерность "А/м2" и в этом смысле действительно является мерой тока, протекающего через единичную площадку, перпендикулярную вектору скорости носителей заряда. Током проводимости называют отношение заряда, пересекающего конечную поверхность S, ко времени:
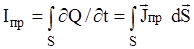 (1.9)
(1.9)
Перейдем теперь от обычной формы закона Ома к дифференциальной форме, для этого выделим внутри проводника с током весьма малых размеров цилиндр, торцы которого перпендикулярны линиям тока (рис.1.4).
 Из-за малости размеров цилиндра будем считать, что плотность тока проводимости постоянна в пределах его торцов, а линии тока параллельны его оси. Согласно закону Ома:
Из-за малости размеров цилиндра будем считать, что плотность тока проводимости постоянна в пределах его торцов, а линии тока параллельны его оси. Согласно закону Ома:
DIпр = DU / R , (1.10)
где: R - сопротивление цилиндра;
DU - напряжение между его торцами, которое равняется: DU = E×Dl.
Выразим сопротивление через удельную проводимость s:
R = Dl / (s×DS), (1.11)
далее подставим (1.10) в (1.9):
DIпр = s×E×DS.
Разделив обе части последнего равенства на DS, получим соотношение: Jпр = s E, которое можно переписать в векторной форме как:
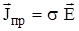 , (1.12)
, (1.12)
где: σ – удельная проводимость среды, которая учитывает силы “внутреннего трения” (столкновения с кристаллической решеткой) носителей тока при движении внутри вещества.
Уравнение (1.12) принято называть законом Ома в дифференциальной форме.
 |
Классификация материальных сред
Формулируются правила разграничения сред по электрофизическим параметрам, характеру их зависимости от интенсивности электромагнитного поля и координат точки наблюдения.
 |
По характеру поведения εа, μа, σ, а также векторов электромагнитного поля 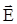 ,
, 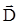 ,
, 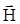 и
и 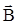 различают следующие виды материальных сред:
различают следующие виды материальных сред:
 называется линейной, если векторы поля
называется линейной, если векторы поля 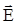 и
и 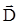 (см. ур-е 1.4), а также
(см. ур-е 1.4), а также 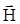 и
и 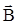 (см. ур-е 1.6) связаны линейной зависимостью, т.е. εа, μа, и σ не зависят от величины векторов поля;
(см. ур-е 1.6) связаны линейной зависимостью, т.е. εа, μа, и σ не зависят от величины векторов поля;
Среда -
называется нелинейной, если не связаны линейной зависимостью, т.е. εа, μа, и σ зависят от величины векторов поля.
 называется изотропной, если векторы поля электромагнитного поля
называется изотропной, если векторы поля электромагнитного поля 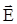 ,
, 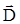 ,
, 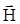 и
и 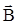 не зависят от направления распространения электромагнитной волны.
не зависят от направления распространения электромагнитной волны.
Среда -
называется анизотропной, если векторы поля зависят от направления распространения электромагнитной волны.
Анизотропия связана с тем, что в определенных веществах существует некоторое специфическое, преимущественное направление. Таким направлением может служить либо какая-то специфическая ось кристаллической решетки, либо направление, в котором приложено внешнее постоянное поле (как, например, у сегнетоэлектриков и ферритов).
 называется однородной, если значения параметров εа, μа, и σ не зависят от пространственных координат x, y, z.
называется однородной, если значения параметров εа, μа, и σ не зависят от пространственных координат x, y, z.
Среда -
называется неоднородной, если εа, μа, и σ меняются от точки к точке и могут быть представлены как функции от пространственных координат.
В зависимости от значения удельной проводимости σ материальные среды подразделяют на три класса:
· диэлектрики, если σ £ 10 –5 См/м;
· проводники, если σ ³ 10 3 См/м;
· полупроводники, если 10 –5 < σ < 10 3 См/м.
Во многих задачах электродинамики реальный проводник или диэлектрик с успехом можно заменить на идеализированный. В этом случае используются понятия:
- идеальный проводник, σ = ∞;
- идеальный диэлектрик, σ = 0.
В качестве примера, ниже приведена таблица значений удельной проводимости (табл.1.1.) для некоторых материальных сред.
Таблица 1.1 –Удельные проводимости некоторых веществ
| Проводники | Диэлектрики | Полупроводники | |||
| Материал | σ, См/м | Материал | σ, См/м | Материал | σ, См/м |
| Серебро Медь Алюминий Железо Свинец | 6,14×107 5,65×107 3,54×107 1,0×107 0,48×107 | Кварц Мрамор Слюда Стекло Дерево | 2×10-17 ~ 10-8 ~ 10-13 ~ 10-12 ~ 10-9 | Земля сухая Земля влажная Вода пресная Вода морская | ~ 10-3 ~ 10-2.5 ~ 2×10-4 ~ 3¸5 |
 |
Дата: 2018-12-21, просмотров: 804.