Формулируются закон полного тока. Вводится понятие тока смещения. Рассматривается характер обобщения закона полного тока.

В начале 19 века датский физик Х. Эрстед установил важнейший для теории электромагнетизма экспериментальный факт, который заключается в том, что протекание электрического тока по проводнику приводит к возникновению в окружающем пространстве магнитного поля (например, пространственная ориентация магнитной стрелки компаса вблизи проводника с током).

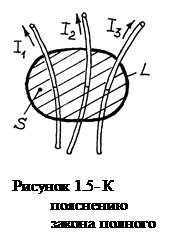На основании открытия Эрстеда, Ампер сформулировал закон полного тока:

Циркуляция по контуру L вектора напряженности магнитного поля Н, вызванного протеканием токов I₁, I₂, I₃,…, равна полному току I _å :

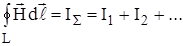         .    (1.13)

Или согласно (1.9):

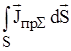= ,                  (1.14)

где: S – поверхность, ограниченная контуром L.

Максвелл дополнил закон Ампера, впервые предположив, что закон полного тока справедлив не только для постоянных полей, но и для переменных полей, если к току проводимости добавить еще один ток, названный им током смещения. Выясним характер его возникновения. Из практики известен факт протекания переменного электрического тока по цепи, содержащей конденсатор (см.рис.1.6.). Это означает, что ток течет не только  по  проводнику  (I_пр),  но и по 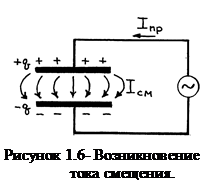прост-ранству между обкладками конденсатора,  в   котором    отсутствуют какие-либо носители   электрического заряда.

Поэтому, можно предположить, что в рассматриваемой области протекает некий ток, природа которого принципиально отлична от природы тока проводимости, изученного Вами ранее (например, в курсе общей физики), поскольку этот ток обусловлен не движением электрических зарядов, а движением материи между обкладками конденсатора в форме поля. Данный ток, получивший название тока смещения, вызван существованием переменного электрического поля:

                        .

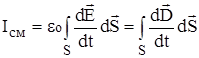По аналогии с (1.9) можно ввести понятие плотности тока смещения:

                                 .

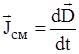Поскольку (см.ур-е.1.7) 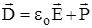, то:

                                 .

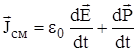Следовательно, ток смещения фактически состоит из двух составляющих:

1.) 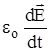 - плотность электрического тока смещения в вакууме. Этот ток образован изменением во времени напряженности электрического поля.

2.) 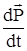 - плотность электрического тока поляризации. Этот ток образован попеременным смещением в атомах вещества связанных зарядов (например, смещением орбит электронов относительно положительно заряженных ядер атомов).

Отличительной особенностью тока проводимости от тока смещения является следующее: ток проводимости связан с движением свободных электрически заряженных частиц под действием электрического поля, тогда как ток смещения определяется лишь изменением во времени вектора электрической индукции.

С учетом изложенного, закон полного тока для переменных полей, называемый обобщенным законом полного тока или 1-ым уравнением Максвелла в интегральной форме, запишется следующим образом:

.   (1.15)

Циркуляция вектора напряженности магнитного поля Н по любому замкнутому контуру L равна сумме истинного электрического тока и тока смещения, протекающих сквозь поверхность, ограниченную этим контуром.

Уравнение (1.15) записано в интегральной форме, т.е. в нем магнитное поле в некоторой области связывается с токами, имеющимися в этой области.

Однако во многих случаях представляет интерес связь между векторами поля в данной точке с токами (или зарядами) действующих в этой же точке. Математически это означает, что необходимо перейти от интегральной формы представления к дифференциальной.

Чтобы это осуществить с 1-ым уравнением Максвелла, используем теорему Стокса (известную из высшей математики).

Тогда:

,

или: 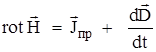      .           (1.16)

Уравнение (1.16) называют 1-ым уравнением Максвелла в дифференциальной форме.