Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

 Второе уравнение Максвелла

Формулируется закон Фарадея и характер

обобщения этого закона, сделанный Максвеллом.

S

В 1831 г. М. Фарадей экспериментально обнаружил возникновение напряжения на концах катушки, помещенной в переменное магнитное поле и на основании своих опытов сформулировал закон электромагнитной индукции (закон Фарадея):

Электрический ток I_пр, индуцируемый в замкнутом проводнике с сопротивлением R, равен скорости убывания магнитного потока Ф, проходящего через поверхность S, ограниченную контуром проводника L.                   I_пр R = 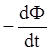.                         (1.17)

Из курса общей физики связь между магнитным потоком и вектором магнитной индукции определяется выражением:

,

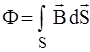тогда:    I_пр R = – 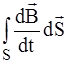.                                                    (1.18)

Максвелл обобщил закон Фарадея, придав термину “контур” более широкий смысл. В формулировке Фарадея ”контур” – это замкнутая цепь проводника (проволочки), в формулировке Максвелла “контур” – это произвольно расположенная в пространстве замкнутая линия (проведенная, например, частично в диэлектрике и частично в проводнике ).

Представим (1.18) в более общем виде. Поскольку ток проводимости (см.ур-е.1.9) есть: 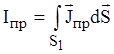, то предположив, что плотность электрического тока  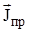распределена равномерно по поперечному сечению проводника S₁, можно записать в этом случае:

,

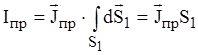Наконец, используя закон Ома в дифференциальной форме 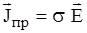, окончательно получаем:

,

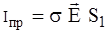где: σ – удельная проводимость.

Из курса общей физики известно, что сопротивление цилиндрического проводника длиной l (см.рис.1.8.) определяется как: R = 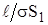, или в общем виде (при замкнутом контуре L):

                     R = .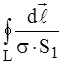

Тогда получаем:

               .

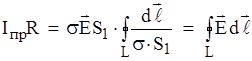И окончательно:

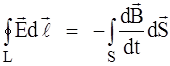              .                             (1.19)

Это и есть второе уравнение Максвелла в интегральной форме:

Циркуляция вектора напряженности электрического поля Е (т.е. электродвижущая сила) по любому замкнутому контуру L равна скорости изменения магнитного потока, пронизывающего этот контур с обратным знаком.

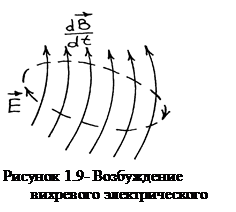Уравнение (1.19) показывает, что изменение во времени вектора магнитной индукции, возбуждает в пространстве вихревое электрическое поле (см.рис.1.9).

     Используя теорему Стокса, запишем 2-ое уравнение Максвелла в дифферен-циальной форме:

 

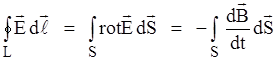
Окончательно:        

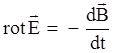                                        (1.20)

 

Теорема Гаусса. Третье и четвертое уравнения

Максвелла

Формулируются теоремы Гаусса для электрической и магнитной индукции и характер обобщения этих теорем, сделанных Максвеллом. Дается физическая трактовка непрерывности магнитных силовых линий.

В электростатике известна теорема Гаусса, полученная на основе экспериментальных данных и устанавливающая связь между вектором электрической индукции 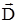 и величиной порождающего его электрического заряда q.

Теорема Гаусса для электрической индукции :

Поток вектора электрической индукции 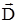 через любую замкнутую поверхность S равен электрическому заряду, заключенному внут-ри этой поверхности.

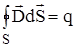              .            (1.21)

Данное выражение устанавливает:

- источниками силовых линий электрического поля могут являться только электрические заряды.

- силовые линии вектора электрической индукции выходят (начинаются) на положительном заряде и входят (заканчиваются) на отрицательном заряде. Т.е. силовые линии вектора 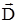 имеют исток и сток.

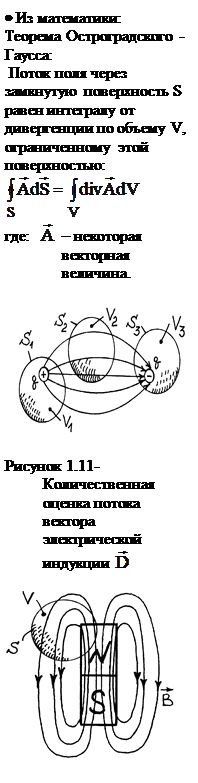
Количественно поток вектора электрической индукции через некоторую замкнутую поверхность S можно оценить числом пересекающих эту поверхность силовых линий. Причем:

- если число входящих линий больше выходящих, то поток считается отрицательным;

- если число входящих линий меньше выходящих, то поток считается положительным.

Поясним сказанное рис.1.11. Для соответствующих объемов V₁, V₂ и V₃ имеем:

;         ;            .

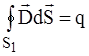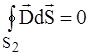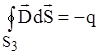  Максвелл обобщил теорему Гаусса, предложив рассматривать ее не только для постоянных полей, но и для переменных полей.

Представим (1.21) в более общем виде. Если в некотором замкнутом объеме V, ограниченном поверхностью S заключено несколько электрических зарядов, то совокупный заряд в этой области представляется через объемную плотность электрического заряда ρ:

              .

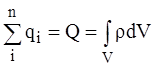Тогда:

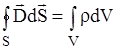              .                                        (1.22)

Полученное выражение носит название 3-го уравнения Максвелла : в интегральной форме:

Поток вектора электрической индукции через любую замкнутую поверхность S равна сумме зарядов в объеме V , ограниченном этой поверхностью.

 

Для того, чтобы записать 3-е уравнение Максвелла в дифференциальной форме используем теорему Остроградского-Гаусса.

Тогда:

,

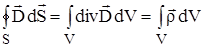или

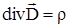                   .                                                   (1.23)

 

Уравнение (1.23) носит название 3-го уравнения Максвелла в дифференциальной форме.

     Из курса общей физики Вам известен экспериментальный факт, что силовые линии магнитного поля независимо от того, создано ли это поле постоянным магнитом или катушкой с переменным током, образуют в пространстве замкнутые линии (например, опыт с железными опилками и постоянным магнитом из школьной программы по физике).

Расположим внутри области существо-вания магнитного поля произвольный объем V, ограниченный поверхностью S. Из замкнутости силовых линий следует, что число входящих линий всегда будет равно числу входящих. Следовательно поток вектора магнитной индукции будет равен нулю. Этот факт закреплен в теореме Гаусса для магнитной индукции :

Поток вектора магнитной индукции В через любую замкнутую поверхность S равен нулю:

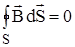     .                     (1.24)

Уравнение (1.24) устанавливает:

- силовые линии вектора магнитной индукции всегда непрерывны, т.е. образуют замкнутые линии.

- в природе не существует магнитных зарядов.

Уравнение (1.24) кроме того, носит название 4-го уравнения Максвелла в интегральной форме.

Используя теорему Остроградского-Гаусса представим 4-ое уравнение Максвелла в дифференциальной форме:

 

                   ,

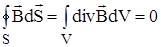Или:          

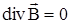                                                    (1.25)