Получим уравнения конических сечений в полярной системе координат, ось которой совпадает с главной осью кривой, а полюс находится в фокусе.
Поместим полюс в фокус параболы. Имеем:
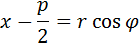
(связь декартовых и полярных координат) и
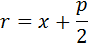
(директориальное свойство параболы). Таким образом,
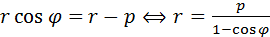 .
.
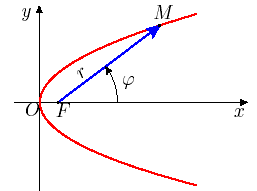
Рис. 23
Поместим полюс в левый фокус эллипса. Имеем: 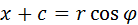
(связь декартовых и полярных координат) и r = ε x + a
(выражение для левого фокального радиуса). Таким образом,
r = ε (r cosφ-c) + a⟺r(1- εcosφ) = a- ε c = p,
так что 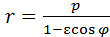 .
.
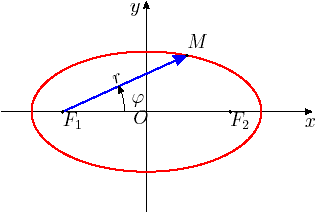
Рис. 24
В случае гиперболы поместим полюс в правый фокус и ограничимся рассмотрением правой ветви гиперболы. Имеем:r = ε x – a , x – c = rcosφ
откуда получаем 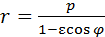 .
.
Таким образом, парабола, эллипс и гипербола (вернее, одна ее ветвь) задаются в полярных координатах одним и тем же уравнением.
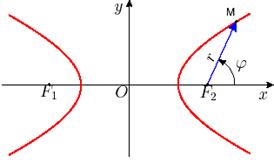
Рис. 25
Парабола, эллипс и гипербола как конические сечения
Каждая из трех указанных линий является плоским сечением некоторого прямого кругового конуса. Если секущая плоскость параллельна одной из образующих конуса, то в сечении получается парабола.
На чертеже:
π — секущая плоскость, параллельная одной из образующих конуса;
S — вершина конуса;
сфера касается конуса по окружности, лежащей в плоскости σ, и секущей плоскости в точке F;
l — линия пересечения плоскостей πи σ;
X — произвольная точка сечения конуса плоскостью π;
Y — точка пересечения образующей SX с плоскостью σ;
Z — проекция точки X на прямую l.
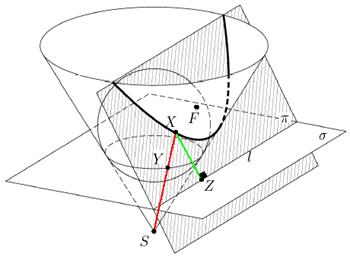
Рис. 26
XF = XY как касательные к сфере. Точки Y и Z лежат в плоскости σ, угол между XY и σ равен углу между образующей конуса и плоскостью, перпенди-кулярной его оси.
Угол между XZ и σ равен углу между плоскостями π и σ. В силу выбора плоскости π эти углы равны, так что XY = XZ как наклонные, образующие равные углы с плоскостью σ. Поэтому XF = XZ, и точка X лежит на параболе с фокусом F и директрисой l.
Если секущая плоскость π пересекает все образующие конуса и не перпен-дикулярна его оси, то в сечении получается эллипс.
На чертеже:
π — секущая плоскость, пересекающая все образующие конуса;
S — вершина конуса;
две сферы касаются конуса по окружностям, лежащим в параллельных плоскостях  и
и  (на чертеже не изображены), и секущей плоскости π в точках
(на чертеже не изображены), и секущей плоскости π в точках 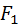 и
и  ;
;
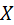 — произвольная точка сечения конуса плоскостью π;
— произвольная точка сечения конуса плоскостью π;
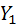 ,
, 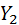 — точки пересечения образующей SX с плоскостями
— точки пересечения образующей SX с плоскостями 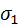 и
и 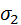 .
.
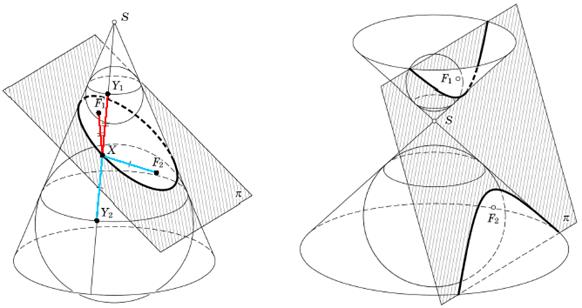
Рис. 27
Имеем 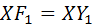 ,
, 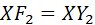 (равенство касательных к сфере), так что
(равенство касательных к сфере), так что
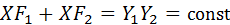 , т.е. точка X лежит на эллипсе с фокусами
, т.е. точка X лежит на эллипсе с фокусами 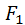 и
и  ;
;
Отметим, что прямые 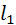 и
и 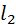 , получающиеся при пересечении плоскостей
, получающиеся при пересечении плоскостей 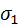 и
и 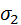 ;плоскостью π, являются директрисами эллипса [докажите самосто-ятельно].
;плоскостью π, являются директрисами эллипса [докажите самосто-ятельно].
Если секущая плоскость π параллельна двум образующим конуса, то в сечении образуется гипербола.
Кривые второго порядка
Парабола, эллипс и гипербола задаются уравнениями второй степени. Общий вид многочлена второй степени от двух переменных
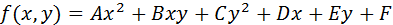 .
.
Кривые второго порядка — это линии на плоскости, задаваемые уравнениями вида
f(x, y) = 0.
Парабола, эллипс и гипербола — примеры кривых второго порядка.
Теорема. Уравнение кривой второго порядка может быть преобразовано посредством замены координат, состоящей из сдвига начала координат и поворота координатных осей, к одной из следующих девяти канонических форм.
I. Эллиптический тип
I.1. Эллипс 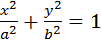
I .2. Точка 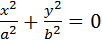
I.3. Пустое множество 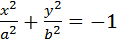
II. Гиперболический тип
II .1. Гипербола 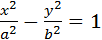
II.2. Пара пересекающихся прямых 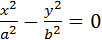
III. Параболический тип
III.1. Парабола 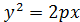
III.2. Пара параллельных прямых 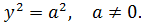
III.3. Пустое множество 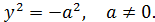
III.4. Пара совпадающих прямых 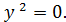
Предел функции
Определение предела. Окрестностью точки X0 называется любой интервал с центром в точке X0
Число A называется пределом функции f (x) в точке X0, если для любого сколь угодно малого числа 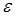 >0 найдется такое число
>0 найдется такое число 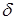 > 0 (вообще говоря, зависящее от
> 0 (вообще говоря, зависящее от 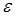 ), что для всех X таких, что
), что для всех X таких, что 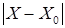 <
< 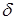 , X
, X 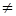 X0, выполняется неравенство
X0, выполняется неравенство 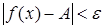 .
.
Операции над пределами функций. Пусть функции f(x) и g(x) определены в некоторой окрестности точки X0 и кроме того, 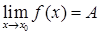 ,
, 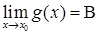 . Тогда:
. Тогда:
1. Предел суммы (разности) этих функций равен сумме (соответственно, разности) их пределов, т.е.
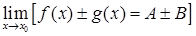 .
.
2. Предел произведения функций равен произведению их пределов, т.е.
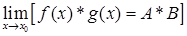 .
.
3. Предел частного функций равен частному их пределов (при условии B 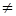 0), т.е.
0), т.е.
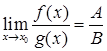 .
.
Отсюда, в частности, вытекает, что постоянный множитель можно выносить за знак предела функции, т.е.
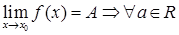 :
: 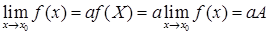 .
.
Предел функции на бесконечности
Пусть функция f(x) определена на бесконечном промежутке (a;+ 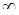 ).
).
 Число A называется пределом функции f(x) при x
Число A называется пределом функции f(x) при x 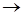
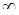 , если для любой положительной бесконечно большой последовательности
, если для любой положительной бесконечно большой последовательности
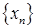 ( т.е. xn
( т.е. xn 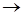 +
+ 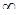 , n
, n 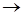
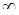 ) последовательность
) последовательность 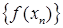 соответствующих значений функции сходится к A.
соответствующих значений функции сходится к A.
Обозначение 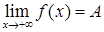 .
.
Односторонние пределы
 Пусть функция f(x) определена в правой полуокрестности точки x0, т.е. на некотором интервале (x0,x0+
Пусть функция f(x) определена в правой полуокрестности точки x0, т.е. на некотором интервале (x0,x0+ 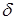 ), где
), где 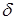 >0. Тогда говорят, что число A называется пределом функции f(x) справа в точке x0 (или правосторонним пределом), если для любой последовательности
>0. Тогда говорят, что число A называется пределом функции f(x) справа в точке x0 (или правосторонним пределом), если для любой последовательности 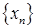 , сходящейся к x0 и такой, что все ее члены больше, чем x0, соответствующая последовательность значений функции
, сходящейся к x0 и такой, что все ее члены больше, чем x0, соответствующая последовательность значений функции 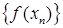 сходится к числу A.
сходится к числу A.
Обозначения: 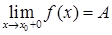 или
или 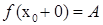 .
.
Замечательные пределы
Первый замечательный предел
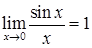
Второй замечательный предел
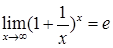
Часто используются следующие следствия из обоих замечательных пределов:
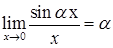 ,
, 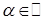 ;
;
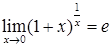 ,
, 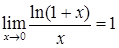 ,
, 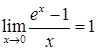 .
.
Следствия:
1. 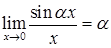 ;
;
2. 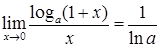 ;
;
3. 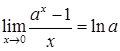 ;
;
4. 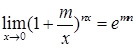 ;
;
5. 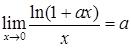 ;
;
Непрерывность функции в точке
 Функция f(x) называется непрерывной в точке x0, если она определена в некоторой окрестности этой точки и
Функция f(x) называется непрерывной в точке x0, если она определена в некоторой окрестности этой точки и 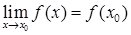
Дата: 2018-12-21, просмотров: 363.