Касательная к параболе — это прямая, непараллельная оси параболы, имеющая с параболой одну общую точку.

Пусть( 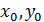) — точка касания параболы  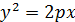и прямой

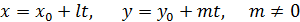
Имеем: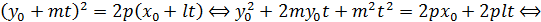

⟺

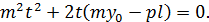
Это квадратное уравнение должно иметь один (двойной) корень, что возможно лишь при выполнении условия:

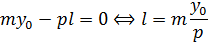
Каноническое уравнение касательной имеет вид:

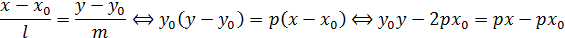
и окончательно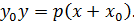

Касательная к эллипсу (гиперболе) — это прямая, имеющая с эллипсом (гиперболой) одну общую точку.

Пусть( 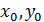) — точка касания эллипса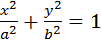

и прямой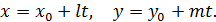

Имеем: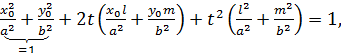    

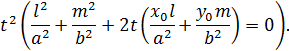
Это квадратное уравнение должно иметь один (двойной) корень, что возможно при выполнении условия

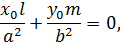
так что можно положить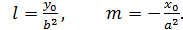

Каноническое уравнение касательной к эллипсу имеет вид

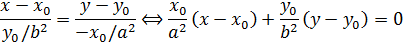
откуда, учитывая соотношение 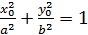, получаем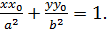

Аналогично получаем уравнение касательной к гиперболе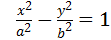

в точке ( ):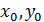

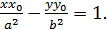
Оптические свойства конических сечений

Теорема. Оптическое свойство эллипса: фокальные радиусы произвольной точки 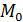эллипсасоставляют равные углы с касательной к эллипсу в точке .

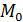Физическая интерпретация: если в фокусе эллипса поместить точечный источник света, а эллипс считать зеркалом, то отраженный эллипсом луч попадет во второй фокус.

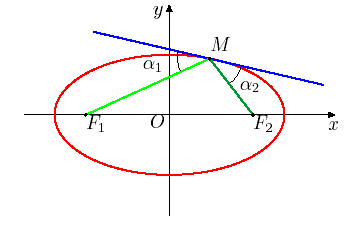
Рис. 18

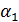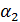Найдем синусы углов и , которые фокальные радиусы произвольной точки 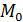( 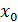, 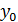) составляют с касательной к эллипсу в точке .

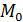Расстояние 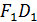от фокуса 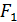(- c, 0) до касательной, имеющей уравнение

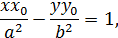
равно   ,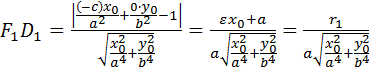

так что  .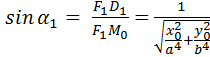

Аналогично получаем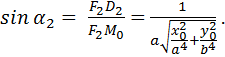

Таким образом, . ►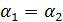

Теорема. Оптическое свойство гиперболы: фокальные радиусы произвольной точки 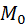гиперболы составляют равные углы с касательной к эллипсу в точке .

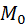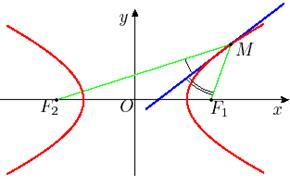
Рис. 19

Теорема. Оптическое свойство параболы: касательная к параболе в каждой точке 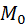составляет равные углы с фокальным радиусом точки 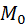и с осью параболы.

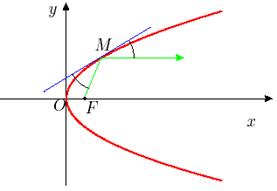
Рис. 20

Уравнения параболы, эллипса, гиперболы,  отнесенные к вершине

Рассмотрим две прямоугольные системы координат с попарно параллельными осями и различными началами: Oxy и O ′ x ′ y ′ . Введем обозначения:

r — радиус-вектор точки M в Oxy,

r ′— радиус-вектор точки M в O ′ x ′ y ′ ,

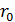,— радиус-вектор точки O ′в Oxy.

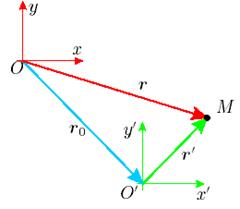
Рис. 21

Очевидно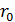,r = + r′.

В координатной форме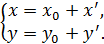

Пусть O ′ x ′ y ′— каноническая система координат эллипса

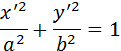
Oxy — система координат, начало которой совпадает с левой вершиной эллипса; тогдаx = x ′ + a, y = y ′

и уравнение эллипса в системе Oxy имеет вид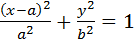

Преобразуем: ,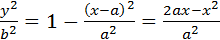

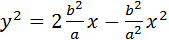
поскольку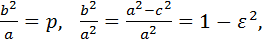

получаем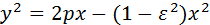

Аналогично, уравнение гиперболы в системе координат, начало которой находится в правой вершине гиперболы, имеет вид

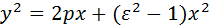
Таким образом, все три типа кривых задаются одним и тем же уравнением

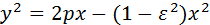
При фиксированном p и изменяющемся ε∈[0,+∞) мы последовательно, получаем:

при ε = 0 окружность;

при ε∈(0, 1) эллипс;

при ε= 1 параболу;

приε∈(1,+∞) гиперболу.

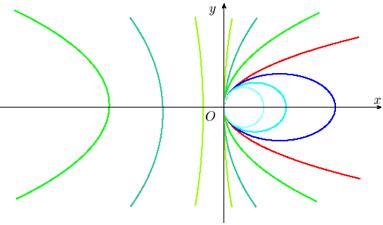
Рис. 22