Смешанным произведением векторов называется такое произведение, при котором 2 вектора перемножаются векторно, полученный при этом вектор скалярно умножается на 3-й вектор. В результате получается число.
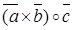- обозначение смешанного произведения.
Свойства смешанного произведения
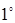. Абсолютная величина смешанного произведения равна объему параллелепипеда, построенного на этих векторах.
Доказательство. Возьмем три некомпланарных вектора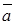 
, 
, 
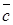. Рассмотрим смешанное произведение.
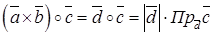, где
,
 |
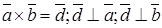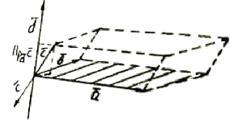Рис. 7
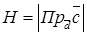по определению векторного произведения 
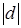- площадь параллелограмма,
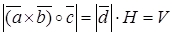- Объем параллелепипеда.
. Круговая (циклическая) перестановка векторов не меняет смешанного произведения, при изменении порядка следования векторов смешанное произведение меняет знак на противоположенный.
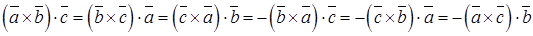
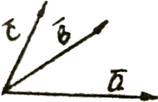
Рис. 8
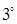. Смешанное произведение обращается в нуль, если перемножаемые векторы компланарны.
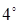. Смешанное произведение векторов, заданных проекциями
, 
, 
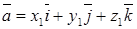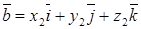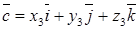, равно
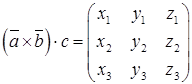
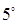. Объем пирамиды, построенного на векторах , 
, 
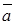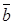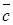равен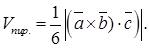 
 |
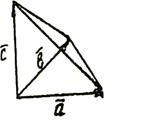Рис. 9
Уравнение плоскости по точке и нормальному вектору
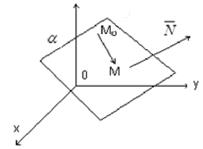Пусть в пространстве 
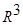дана точка 
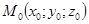и вектор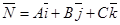 
Рис. 10
Уравнение плоскости 
, проходящей через точку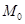 
перпендикулярно заданному вектору 
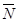определяется уравнением
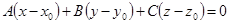
Вектор 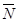, перпендикулярный плоскости , называется нормальным вектором этой плоскости.
Уравнение плоскости по трем точкам
Пусть в пространстве 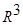даны три точки 
, 
, 
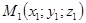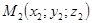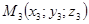, не лежащие на одной прямой. Выберем в этом пространстве произвольную точку 
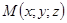и построим три вектора 
, 
, 
.
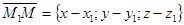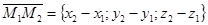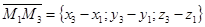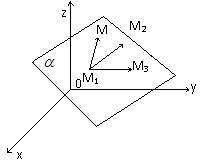
Рис. 11
Предположим, что точка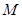 
лежит на плоскости (рис. 11), проходящей через заданные точки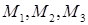 
. Тогда векторы 
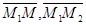и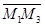 
лежат на этой плоскости. Следовательно, 
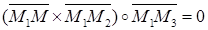Û
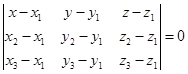(1)
Общее уравнение плоскости
Уравнение первой степени относительно переменных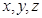 
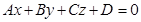(2)
будем называть общим уравнением плоскости.
Рассмотрим некоторые частные случаи этого уравнения:
1) 
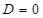. Тогда плоскость 
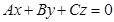проходит через начало координат, так как точка 
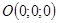принадлежит этой плоскости при любых значениях 
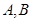и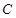 
;
2) 
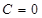. Уравнение плоскости запишется в виде 
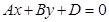. Так как старшие коэффициенты 
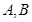и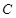 
являются проекциями нормального к плоскости вектора 
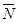, то вектор 
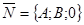перпендикулярен этой плоскости. Но вектор 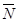перпендикулярен и координатной оси 
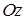. Следовательно, рассматриваемая плоскость параллельна оси ;
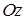3) если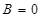 
, то плоскость 
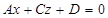параллельна оси 
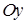(доказать самостоятельно);
4) если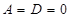 
, то плоскость проходит через начало координат и параллельна оси 
. Следовательно, плоскость 
проходит через ось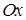 
;
5) если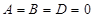 
, то 
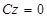Û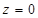 
совпадает с плоскостью 
.
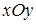Кривые второго порядка
Парабола
Парабола - линия, которая в прямоугольной декартовой системе координат Oxy имеет уравнение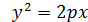 
(1)
Уравнение (1) иногда называют каноническим уравнением параболы.
Теорема. Парабола представляет собой множество точек, равноудаленных от данной прямой (директрисы параболы) и данной точки (фокуса параболы), не лежащей на директрисе.
· Пусть парабола задана уравнением (1). Имеем:
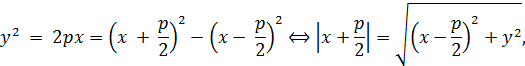
т.е. точка (x, y) параболы равноудалена от прямой x = - p/2 и точки (p/2, 0), котораяявляется фокусом параболы, поскольку при x = p/2 имеем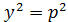 
.
Обратно, рассмотрим прямую x = - p/2 и точку F(p/2, 0). Точка M(x, y) удалена отуказанной прямой на расстояние |x+p/2|, а от точки F — на расстояние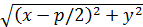 
.
Условие равенства этих расстояний
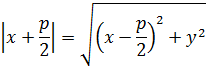
после возведения в квадрат и несложных преобразований дает уравнение (1). ►
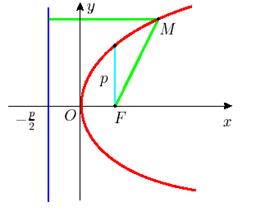
Рис. 12
Основные термины, связанные с параболой:
(1) ось Ox — ось параболы;
(2) фокальная хорда — отрезок с концами на параболе, проведенный через
фокус перпендикулярно оси;
(3) p — (фокальный) параметр (равен половине длины фокальной хорды);
(4) p/2 — фокусное расстояние
(5) точка F(p/2, 0) — фокус;
(6) прямая x = -p/2 — директриса.
Эллипс
Эллипс — это линия, которая в некоторой прямоугольной декартовой системе координат Oxy имеет уравнение
Указанная система координат называется канонической, уравнение (2) — каноническим уравнением эллипса.
Основные термины, связанные с эллипсом:
(1) a — большая полуось;
(2) b — малая полуось;
(3) 
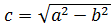— линейный эксцентриситет;
(4) точки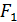 
(-c, 0), 
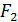(c, 0) — фокусы;
(5) 2c — фокусное расстояние;
(6) ε = c/a< 1 — (числовой) эксцентриситет;
(7) прямые x = ± a/ ε— директрисы;
(8) ось OX — большая (фокальная) ось;
(9) ось OY — малая ось;
(10) фокальная хорда — отрезок с концами на эллипсе, проведенный через
фокус перпендикулярно фокальной оси;
(11) p =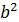 
/a — (фокальный) параметр(равен половине длины фокальной
хорды);
(12) точки (±a, 0), (0,±b) — вершины эллипса;
 |
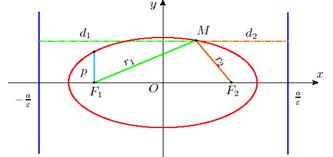(13) точка O(0, 0) — центр эллипса.
Рис. 13
Пусть M(x, y) — произвольная точка эллипса. Отрезки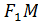 
, 
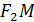называ-ются фокальными радиусами точки M.
Теорема. Фокальное свойство эллипса: Эллипс является множеством точек, сумма расстояний от которых до фокусов постоянна: 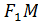+ 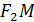= 2a.
● Рассмотрим эллипс
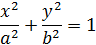
Фокальные радиусы произвольной точки M(x, y) эллипса равны
Имеем
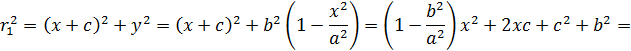
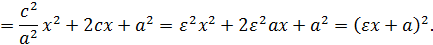
Поскольку 
имеем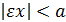 
, так что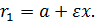 
Аналогично находим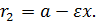 
Следовательно,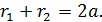 
Обратно, пусть M(x, y) — точка плоскости, для которой сумма 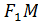+ 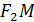постояннаи равна 2a, т.е. 
.
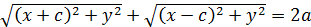Уничтожив радикалы, придем к уравнению
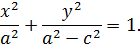
Теорема. Директориальное свойство эллипса: Эллипс является множеством точек, отношение расстояний от которых до фокуса и до соответствующей директрисы постоянно(и равно ε ).
●Расстояния от произвольной точки M(x, y) эллипса до левой и правой директрисы равны
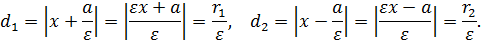
Обратно, если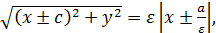 
то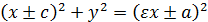 
и поэтому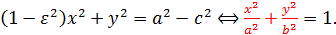 
Гипербола
Гипербола — эта линия, которая в некоторой прямоугольной декартовой системе координат Oxy координат имеет уравнение
Указанная система координат называется канонической, уравнение (3) — каноническим уравнением гиперболы.
Выразим из уравнения гиперболы y:
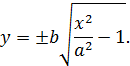
Имеем:
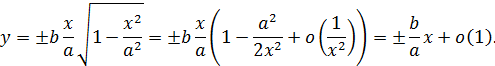
Таким образом, прямые
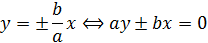
являются асимптотами гиперболы.
Рис. 14
Основные термины, связанные с гиперболой:
(1) a — вещественная полуось;
(2) b — мнимая полуось;
(3) 
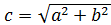— линейный эксцентриситет;
(4) точки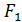 
(-c, 0), 
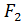(c, 0) — фокусы;
(5) 2c — фокусное расстояние;
(6) ε = c/a> 1 — (числовой) эксцентриситет;
(7) прямые x = ± a/ ε— директрисы;
(8) ось OX — вещественная (фокальная) ось;
(9) ось OY — мнимая ось;
(10) фокальная хорда — отрезок с концами на гиперболе, проведенный через
фокусперпендикулярно фокальной оси;
(11) p =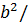 
a — (фокальный) параметр (равен половине длины фокальной
хорды);
(12) точки (± a, 0) — вершины гиперболы;
(13) точка O(0, 0) — центр гиперболы;
(14) прямые ay ± bx = 0 — асимптоты гиперболы.
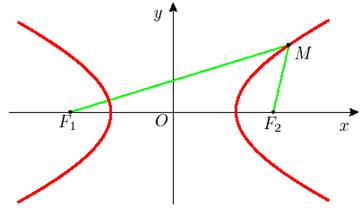
Рис. 15
Пусть M(x, y) — произвольная точка гиперболы. Отрезки 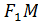, 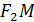называются фокальными радиусами точки M.
Теорема. Фокальное свойство гиперболы: Гипербола является геометрическим местом точек, разность расстояний от которых до фокусов по абсолютной величине постоянна: | 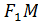- 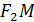| = 2a.
●Рассмотрим гиперболу
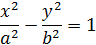
Длины фокальных радиусов точки M(x, y) равны
Имеем
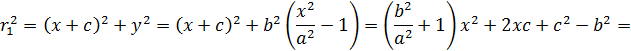
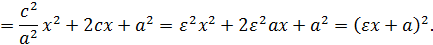
Поскольку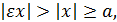 
имеем
Аналогично получаем
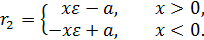
Следовательно,
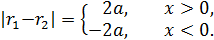
Обратно, пусть M(x, y) — точка плоскости, для которой| 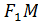- 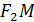| = 2a., т.е.
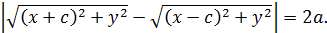
Уничтожив радикалы, придем к уравнению
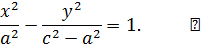
Теорема. Директориальное свойство гиперболы: Гипербола является геометрическим местом точек, отношение расстояний от которых до фокуса и до соответствующей директрисы постоянно (и равно ε ).
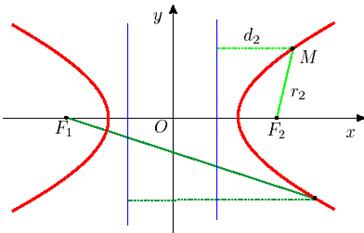
Рис. 16
●Расстояния от произвольной точки M(x, y) гиперболы до левой и правой директрис равны
.
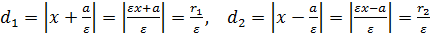Обратно, если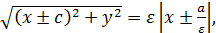
то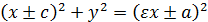
и поэтому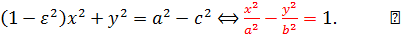 
Наряду с гиперболой, заданной каноническим уравнением
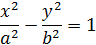
часто рассматривают гиперболу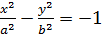 
, называемую сопряженной по отношению к исходной.
Умножая уравнение сопряженной гиперболы на -1, получим каноническое уравнение, в котором роли координатных осей поменялись:
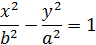
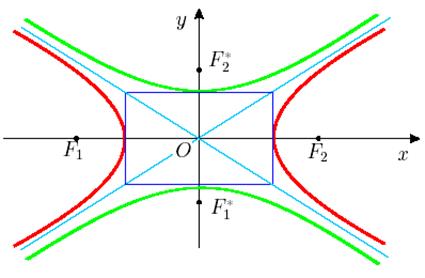
Рис. 17
Дата: 2018-12-21, просмотров: 275.
