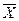Рассмотрим вопросы практического применения ( )-карты и  ( - s)-карты для анализа технологических процессов. Вспомним, что выборочный размах R - это разность между максимальным и минимальным выборочными значениями. Это более простая функция, чем выборочное стандартное отклонение S. Размах был предложен для контроль­ных карт в 30-е годы XX в., когда еще не было при­емлемых подручных средств вычислительной техники. Однако размах не является прямой оценкой 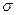. Через R можно оценить  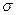при помощи специального коэф­фициента d₂, но менее точно, чем через S. Кроме того, как показывает практика, кажущаяся простота вычисления размаха «в уме» обманчива, здесь часто появляются ошибки, особенно при объемах выборки n > 5. Поэтому, если при построении карты используется микрокалькуля­тор со статистическими функциями или компьютер, то ( 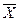- s)-карты предпочтительнее.

Для анализа ( 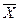- s)-карты проводят оценки «собственного» стандартного отклоне­нии процесса 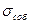. Величина  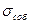характеризует присущий самому процессу, «встроенный» в процесс раз­брос, даже если процесс абсолютно стабилен и нет никаких дестабилизирующих факторов. Этот разброс проявляется в виде разброса значений «внутри мгно­венных выборок», когда, по предположению, процесс стабилен.

Зная оценку 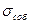, определяют наимень­ший уровень несоответствий, который может обеспе­чить исследуемый технологический процесс. Этот минимум достигается, когда технологический процесс стабилен по  и 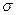 и имеет настройку (т. е. значение ) по центру допуска. Это - нижний предел того уровня несоответствий, который может обеспечить данная технология с данным обору­дованием. По меткому замечанию Дж. Джурапа, выс­казанному им в 1979 г., «самое полезное для специа­листов, планирующих процессы, - знать такие преде­лы в количественной форме».

Этот «оптимистический» предел для данного технологического процесса можно определить из таблицы 1 (Методы менеджмента качества, 2004, № 7, с. 43), где величина Z — это отношение половины ширины поля допуска к величине 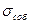. В таблице 1 также указаны доли продукции (в единицах ррm), «вылетающей» за одну границу допуска при нормальном распределении показателя качества и настройке технологического процесса (т. е. ) по цен­тру допуска. Общую долю несоответствующей про­дукции (за пределами обеих границ допуска) при этом получают удвоением табличного значения.

Из таблицы 1 следует, что если величина 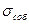 относи­тельно невелика, г. е. превышает, например, 1/8 часть поля допуска, т. е. Z = (половина допуска)/  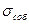= 4, то данная технология не может обеспечить уровень несоответствий меньше 31,686·2=63 ррm, а если Z= (половина допуска)/  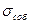= 3,55, то минималь­но возможный уровень несоответствий равен 192,66·2=285 ррm, и т. д. Таким образом, если  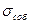относительно велика, то снизить уровень несоответствий можно только путем коренного улучшения самой технологии, чаще всего - оборудования.

Оценку 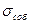 находят по формуле

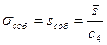                                        ,                                      (92)

где 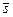- среднее арифметическое от s_j, определяемых по формуле (46);

  с₄ – коэффициент, определяемый объемом подгруппы, значения которого приведены в ГОСТ Р 50779.42 (ИСО 8258-91). Статистические методы. Контрольные карты Шухарта.

Далее находят оценку полного стандартного отклонении про­цесса 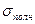. Это - оценка полного разброса исследуемого показателя качества за все наблюдаемое время, в те­чение которого «работали» дестабилизирующие фак­торы. Такую оценку легко получить, если объединить в нее наблюдаемые выборки в одну общую и вычислить характеристику S (т. е. характеристику разброса отно­сительно общего среднего) для этой общей выборки

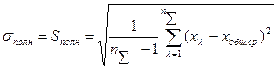                 ,                         (93)

где 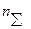 - суммарный объем общей выборки, т. е. сумма объемов всех отдельных выборок;

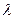 - номер отдельных наблюдаемых значений; соответствует «сквозной нумерации» по всем отдельным выборкам;

X_общ.ср - общее среднее по всем наблюдаемым значениям в общей выборке.

Модельное представление поведения процесса в отдельные периоды времени и общее его представление за большой период времени наблюдения приведено на рисунке 22.

Рисунок 22 - Модельное представление поведения процесса в отдельные периоды времени и общее его представление за большой период времени наблюдения

Здесь показан случай, когда процесс стабилен по «собственной» дисперсии V(X) = 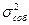=const.

Очевидно, что полное стандартное отклонение процесса всегда больше собственного стандартного отклонения:

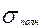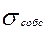                                     >  ,                                       (94)

но вот, на сколько больше, - это и определяет «меру нестабильности» процесса, т. е. «культуру организации технологии». Согласно М. Хэрри и Дж. Лоунеу, соотношение 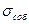 и 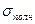 характеризует «относитель­ную эффективность управления за продолжительный период производства».

Если в соответствии с полученными оценками 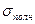 > 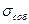на 10% или даже менее 10%, то это близ­кий к стабильному процесс. Или следует сказать аккуратнее: за наблюдаемый период на процесс не действовали сильные дестабилизирующие факторы или они действовали редко - в период одной - двух выборок, но даже эти редкие дестабилизации должны быть хорошо видны по ККШ.

Если же 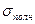≥ 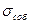, то можно точно утверж­дать, что это существенно нестабильный процесс и его можно улучшить, если найти и ликвидировать в производстве дестабилизирующие причины (факто­ры). Если дестабилизирующие факторы исходят не от технологического оборудования, то его замена ничего не даст и эти факторы сохранят свое негативное влияние на выход процесса.

Однако, если

                    ≤ 0,1 (ширина поля допуска),                   (95)

то процесс может считаться приемлемым с точки зре­ния «вылетов» за пределы допуска, т. е. результирую­щего уровня несоответствий, даже при существенной нестабильности процесса.

Редко, но случается, что 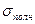 < 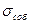. Это происходит из-за того, что и то, и другое – все-таки оценки, а не истинные значения стандартных отклонений. Это – также случай стабильного процесса.

Если нет полной уверенности в том, что процесс со всеми влияющими факторами достаточно хо­рошо изучен, следует продолжать наблюдать за ним при помощи описанных выше ККШ.

Необходимо подчеркнуть, что описанные в предыдущих лекциях ККШ по своей сути являются инструментом для анализа поведения технологического процесса «задним чис­лом», а не инструментом для управления процессом в реальном времени. В самом деле, нельзя по­строить контрольные границы до тех пор, пока нет выборочных данных о процессе. Контрольными картами для управления процессом в ре­альном времени являются адаптивные контрольные карты, которые применяют в случае, когда возможно регулирование процесса и когда необходимо строгое отслеживание стандартных уровней. Это предполагает применение моделей прогноза с различной степенью сложности для предсказания хода процесса по его текущему состоянию и внесения своевременной корректировки при отклонении процесса от стандартного уровня. Поскольку элементы этих моделей существенно зависят от особенностей процесса, адаптивные контрольные карты обычно уникальны и используются в частных случаях. В отличие от контрольных карт Шухарта, эти контрольные карты учитывают предварительные оценки уровней процесса с учетом предположения, что процесс будет развиваться в том же направлении и что во избежание отклонения от предсказанного движения необходима регулярная корректировка.