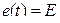4.1. На лабораторном модуле собрать схему рис. 1, используя в качестве ЭДС источника генератор прямоугольных импульсов 
( 
), рассчитанное значение 
; 
нФ; 
мкФ.
4.2. Подключить к генератору осциллограф или ПК. Включить стенд и генератор прямоугольных импульсов. Установить частоту следования импульсов 200 Гц ( Т=5 мс ) и 
В. Отрегулировать развертки и усиление канала Х осциллографа, чтобы на экране помещался один - два периода .
4.3. Снять осциллограммы тока 
, напряжения на ёмкости 
и индуктивности 
.
4.4. Установить значение R из раздела 3, при котором наблюдается апериодический переходный процесс.
4.5. Повторить опыт 3 раздела 4.
4.6. Определить по снятым осциллограммам начальные и установившиеся значения исследуемых величин.
4.7. Результаты измерений занести в табл. 1.
4.8. Установить значение R, соответствующее затухающему колебательному процессу из раздела 3 и снять осциллограммы , 
, 
.
4.9. Определить по снятым осциллограммам коэффициент затухания 
, угловую частоту 
и период затухания колебаний Т.
4.10. Результаты измерений занести в табл. 2.
Таблица 2
|
| Т, с |  , с
|  , с-1
| tпп, с | |
| Включение цепи под действие источника | Расчет | ||||
| Опыт | |||||
| Короткое замыкание источника (E=0) | Расчет | ||||
| Опыт | |||||
5. Контрольные вопросы
5.1. Какой процесс называется переходным? Что называется принужденной и свободной составляющей переходного процесса?
5.2. Сформулируйте законы коммутации.
5.3. Как определяются зависимые начальные условия? Для цепи рис. 8 
В, 
Гн, 
кОм, 
мкФ определить 
и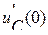 
.
5.4. Для цепи рис. 9 В, кОм, Гн, мкФ определить 
и 
.
5.5. Как по графикам определить постоянную времени? Каков её физический смысл?
5.6. Как составляется характеристическое уравнение и для чего оно необходимо?
5.7. Чем определяется порядок электрической цепи?
5.8. Для цепи рис. 8, В, кОм, Гн, 
мкФ определить корни характеристического уравнения и записать в общем виде решение для тока в цепи.
5.9. Для цепи рис. 9, 
В, 
кОм, 
Гн, 
мкФ определить корни характеристического уравнения и записать в общем виде решение для напряжения на конденсаторе.
5.10. Как по графикам переходного процесса для колебательного режима определить 
- декремент затухания и 
- частоту свободных колебаний цепи?
5.11. Как определяются постоянные интегрирования (на примерах для второго порядка)?
5.12. Какой разряд конденсатора называется апериодическим?
5.13. Какой разряд конденсатора называется колебательным?
Лабораторная работа №7
Исследование цепной модели линии
C распределенными параметрами.
Цель работы
Целью работы является определение параметров длинной линии, эквивалентной цепной схеме, состоящей из четырехполюсников; определение частоты источника напряжения, при которой цепная схема эквивалента заданному отрезку линии, а также исследование распределения действующего значения напряжения вдоль линии в режимах холостого хода и короткого замыкания.
Краткие сведения из теории
Длинную линию с распределёнными параметрами можно представить как схему с бесконечно большим числом элементарных звеньев, обладающих конечными значениями параметров. Такая замена будет давать тем более точные результаты, чем большее число звеньев будет содержать цепная схема.
На рис.1 показана цепная схема, представляющая собой соединение n – го числа симметричных Т – образных четырехполюсников.
При рассмотрении задачи будем полагать, что элементы схемы Т – образных четырехполюсников известны:
; 
,
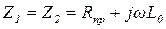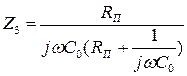где Rпр – продольное активное сопротивление единицы длины линии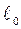 
(например, 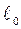= 1 км);
Rп – поперечное активное сопротивление утечки в линии длиной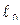 
;
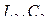– индуктивность и емкость линии длиной .
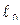Определим параметры длинной линии, имеющей длину 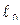, которая эквивалентна одному звену, представляющему симметричный четырехполюсник, из которой построена цепная схема. Решение этой задачи известно и приведено в [1]. Рассмотрим ее решение в нужном нам толковании. Для Т – образной симметрической схемы четырехполюсника основные уравнения его имеют вид:
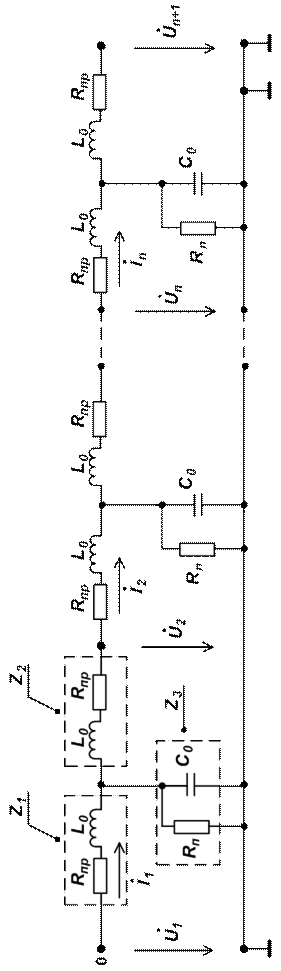
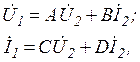(1)
где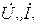 
- напряжение и ток на входе;
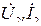- напряжение и ток на выходе;
A, B, C, D – коэффициенты четырехполюсника, причем A = D .
Для длинной линии длины 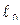связь между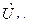 
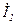и 
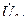
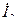(напряжения и токи в конце и в начале линии) определяется уравнениями
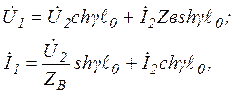(2)
где Z В - волновое сопротивление,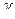 
- постоянная распространения 
, 
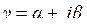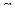- коэффициент затухания падающей волны на единицу длины линии, 
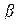- коэффициент фазы, характеризует изменение фазы на единицу длины линии.
Учитывая, что элементы электрической схемы каждого четырехполюсника известны, то:
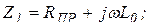
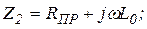
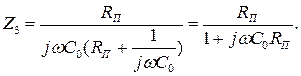
Параметры A , B , C , D, входящих в цепную схему четырехполюсников, выразим через известные значения Z 1 , Z 2 , Z 3 следующим образом [1, стр. 141]:
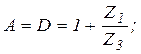
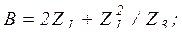
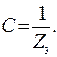(3)
В рассматриваемой задаче по известным значениям A , B , C , D необходимо определить параметры эквивалентной линии. Этими искомыми параметрами, как уже ранее отмечалось, являются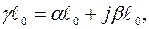 
.
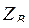Если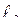 
принять за единицу длины линии, то искомыми параметрами эквивалентной линии являются: 
, 
, .
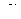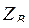Определим теперь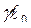 
. Для этого используем соотношения (3) и аналогичные по форме записи уравнения (1) и (2).
Из этой аналогии следует:
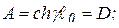
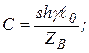
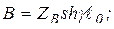
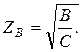(4)
Для определения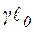 
составим выражения для 
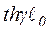на основании (3) и (4),
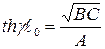. (5)
Как показано в [1], функцию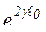 
можно выразить следующим образом:
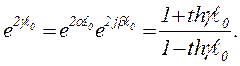(6)
Подставляя в (6) значение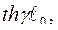 
вычисленное по формуле (5) по известным A , B , C и представляя после вычисления числитель и знаменатель правой части (6) в показательной форме, находим значения 
, 
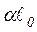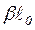, т. е. определяем параметры линии, эквивалентной одному звену Т – образного симметричного четырехполюсника. При этом 
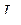и 
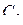представляют собой соответственно индуктивность и емкость линии длиной 
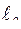и имеют соответственно размерность Гн/м и Ф/м.
Если число звеньев цепной схемы равно n, то длина отрезка эквивалентной длинной линии будет в n – раз больше, т. е. равна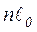 
. Обозначим напряжение и ток на выходе n – го звена через 
, 
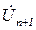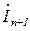. Тогда напряжение и ток на входе первого звена:
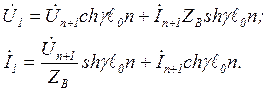
(7)
На основании (7) напряжение и ток на входе k – го звена (k £ n)
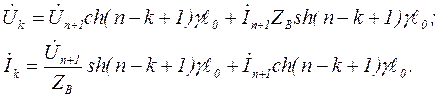(8)
Как видно из (8), для того чтобы определить значение напряжения на входе или выходе любого звена (т. е. рассчитать распределение напряжения или тока вдоль цепной схемы) необходимо знать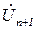 
и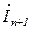 
. Для этого предварительно необходимо провести опыт на определенной частоте по измерению напряжения и тока в конце лини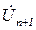и и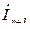 
, либо задать их значения. После чего, используя (8), можно провести расчет в заданной цепной схеме распределение тока и напряжения в разных точках цепной схемы.
Рассмотрим теперь расчет частоты источника синусоидального напряжения на входе линии, при котором цепная схема будет эквивалентна заданному отрезку линии, равному, например, длине четвертьволнового отрезка линии, или полуволновому или любому другому отрезку линии, в который укладывается необходимое число полуволн.
Ответ на этот вопрос легко получить, если рассмотреть холостой ход линии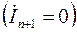 
. При малых потерях аргументы гиперболических косинусов и синусов становятся чисто мнимыми 
.
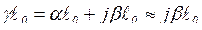Тогда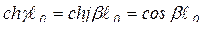 
; 
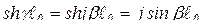. (9)
Для холостого хода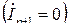 
с учетом (9), получаем
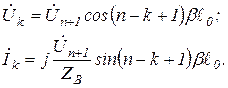(10)
Пусть нас интересует частота питающего напряжения, на которой цепная схема моделирует четвертьволновой отрезок в режиме холостого хода. Ток на входе в этом случае должен иметь максимальное значение, а напряжение стремиться к нулю. Это возможно когда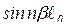 
= 1, т. е. на основании (10) можем записать
; 
;
.
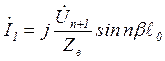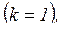
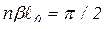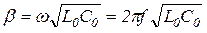Следовательно: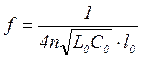 
. (11)
Если удвоить частоту источника синусоидального напряжения, то цепная схема будет эквивалентна полуволновому отрезку линии. При четырехкратном увеличении частоты данная цепная схема будет являться моделью линии, на длине которой указывается полная волна, и т. д.
Ниже на рис. 2 рис. 3 приведены результаты расчёта распределения напряжения и тока вдоль четвертьволнового отрезка линии в различных режимах его работы. При расчете распределения действующих значений напряжения и тока в режиме х.х. по формуле (8) принято U n+1 = 10 В, а при расчете распределения действующего значения напряжения и тока в режиме к.з. принято I n+1 = 1 A. При этом число звеньев принято n = 16 со следующими единичными параметрами длинной линии:
Lo = 390 мкГн/км; Co = 4,7 пФ/км; Rп = 150 кОм/км при различных значениях Rп, равных 1 Ом, 5 Ом, 10 Ом.
Частота питающего напряжения при этом определена по формуле (11) и соответствует f = 11541 Гц.
Рис. 2
Рис. 3
Дата: 2018-11-18, просмотров: 384.
