4.1. Собрать схему рис. 2. Значение тока, протекающего в цепи, определяется с помощью цифрового вольтметра путем измерения напряжения на образцовом резисторе
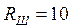Ом; т.е.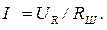 
Измерение сдвига фаз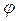 
между 
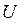и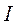 
осуществляется при помощи фазометра.
4.2. Включить ГНЧ (обеспечивает получение синусоидального напряжения с плавной регулировкой частоты) и установить входное напряжение по заданию преподавателя.
4.3. Изменяя частоту генератора в окрестности расчетного значения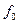 
, найти резонансную частоту цепи 
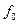по максимальному показанию вольтметра V2 (что соответствует выполнению условия резонанса) или по нулевому показанию фазометра.
4.4. При изменении частоты с интервалом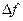 
от резонансной
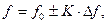
где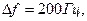 
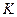= 0, 1, 2, 3, 4, 5;
в пределах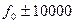 
Гц снять частотные характеристик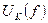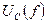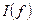и 
; 
; 
и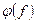 
.
4.5. Экспериментальные данные п. 4.4 занести в табл.1. Построить графики зависимостей (опытные и расчетные)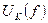 
; 
; 
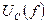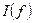и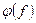 
и сравнить их.
5. Контрольные вопросы
5.1. Как практически можно определить состояние резонанса напряжений в последовательном R , L , C контуре?
5.2. Как определяется частота собственных колебаний контура?
5.3. Почему в момент резонанса не равны напряжения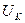 
и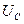 
?
5.4. В сеть переменного тока последовательно включены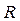 
, L и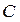 
. Заданы значения R и С. Определить индуктивность катушки L , которую нужно включить в цепь, чтобы на заданной частоте возник резонанс напряжений, если R = 5 Ом, 
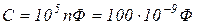, а также во сколько раз напряжение на емкости будет больше входного напряжения на резонансной частоте.
Лабораторная работа №4
Резонанс токов.
Цель работы
Целью работы является практическое знакомство и исследование явления резонанса в цепи, состоящей из параллельно включенных катушки индуктивности и емкости.
Краткая теория
В режиме резонанса в цепи, предоставляющей параллельное соединение катушки индуктивности и конденсатора, в катушке и конденсаторе возникают токи, многократно превышающие ток на входе цепи (отсюда и название - резонанс токов).
Рассматриваемая электрическая цепь, показанная на рис.1, представляет собой параллельный колебательный контур с потерями энергии, обусловленными резисторами. Для упрощения проведения испытаний резонанса в параллельном контуре в цепь введены одинаковые по модулю величины резисторы R .
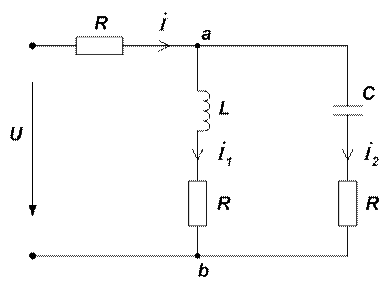
Рис. 1
Эквивалентная проводимость параллельного контура между точками «а» и «б» определяется выражением
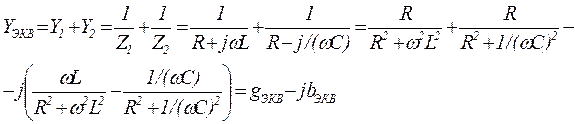(1)
Условие резонанса определяется равенством нулю мнимой части входной проводимости параллельного контура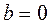 
, т.е из (1) получаем (заменяя ω на ωР)
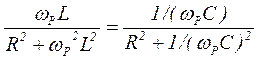(2)
В этом случае входное сопротивление будет чисто активным, а в идеальном случае, когда R → 0, стремится к бесконечности.
Из (2) получаем значение резонансной частоты параллельного контура при условии, если R во всех ветвях одинаковы по величине.
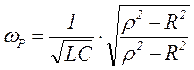, (3)
где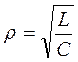 
- волновое (характеристическое) сопротивление. В идеальном контуре, когда R → 0, как видно из (3) 
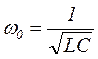, т.е. такое же значение частоты как и в последовательном контуре.
Определим теперь эквивалентное сопротивление параллельного контура относительно точек а, б (см. рис. 1) на резонансной частоте используя (1), учитывая что реактивная проводимость b при резонансе равно нулю.
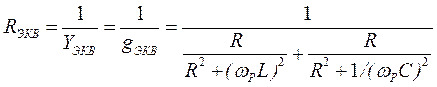(4)
Подставляя в (4) значение ωР , вычисленное по формуле (3), получаем возможность рассчитать эквивалентное сопротивление рассматриваемого контура. (Если активные сопротивления, включенные в ветвях, не равны между собой, то получается более сложное выражение для RЭКВ и ωР ).
Из (4) видно, что в идеальном контуре, когда R = 0, то RЭКВ → ∞.
Ток в неразветвленной части при резонансе можно определить следующим образом (учитывая, что сам контур обладает чисто активным сопротивлением):
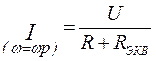, где I, U – действующие значения. (5)
Токи в параллельных ветвях также легко определяются на основании (5) по закону Ома
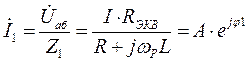
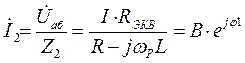
Сдвиг по фазе между токам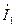и 
и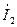 
Δφ = φ1 - φ2 = 1800 (при малых значениях R, т.е. когда ωРL >> R и 1/ωРС >> R ).
Как видно из рис. 1, ток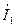 
при резонансе должен отставать от напряжения 
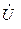по фазе почти на 900, а ток 
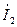- опережать напряжение 
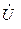почти на 900 при малых значениях R.
3. Задание для самостоятельной подготовки
3.1. По учебнику [1] следует дополнительно ознакомиться с основами теории параллельного колебательного контура.
3.2. Рассчитать электрическую цепь (рис. 1) при напряжении 0 < U ≤ 1 (задается преподавателем), С = 100 нФ, L = 50 мГн, R = 10 Ом. Расчету подлежат следующие параметры:
- резонансная частота идеального контура f0=ω0/2π, Гц;
- резонансная частота исследуемого контура fР, Гц;
- волновое сопротивление исследуемого контура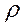 
, Ом;
- эквивалентное сопротивление исследуемого контура при резонансе (ω = ωР) RЭКВ , Ом;
- ток в неразветвленной части цепи на частоте резонанса (ω = ωР) I, А;
3.3. Рассчитать и построить график зависимости ZЭКВ = 1/YЭКВ при изменении частоты от резонансной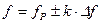 
, где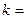 
0, 1, 2, 3, 4, 5, 
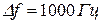, в пределах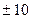 
.
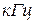3.4. Рассчитать токи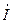 
, 
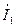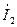, и построить на комплексной плоскости векторную диаграмму для токов , , 
, 
.
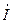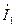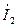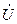3.5. По графику зависимости ZЭКВ от частоты определить добротность контура (Q = fР/Δf)
Расчетные данные п. 3.4 занести в табл. 1.
Таблица 1
| Частота, Гц | Опыт | Расчет | ||||
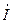 , А
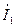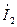|  , А
|  , А
| I, А | I1, А | I2, А | |
| fР – 1000 | ||||||
| fР - 800 | ||||||
| fР - 600 | ||||||
| fР - 400 | ||||||
| fР - 200 | ||||||
| fР | ||||||
| fР + 200 | ||||||
| fР + 400 | ||||||
| fР + 600 | ||||||
| fР + 800 | ||||||
| fР + 1000 | ||||||
4. Методические указания по проведению работы
4.1. Работа выполняется на лабораторном модуле универсально измерительного лабораторного стенда. С помощью перемычек собирается электрическая цепь (рис. 2), которая подключается к генератору синусоидально изменяющегося напряжения во времени в диапазоне частот от 200 Гц до 10 кГц.
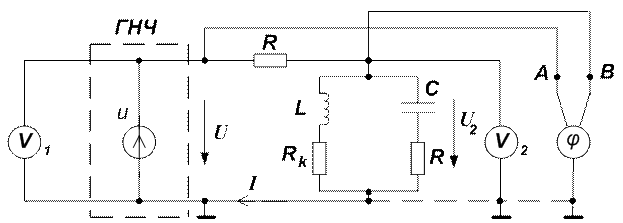
Рис. 2
Значения токов в ветвях определяются с помощью цифрового вольтметра путем измерения падения напряжения на образцовых резисторах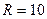 
Ом, с последующим вычислением тока по закону Ома, т.е. 
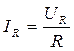. Измерения сдвига фаз 
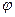между напряжением на контуре 
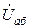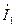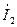и токами и осуществляется с помощью электронного фазометра (вначале провод А фазометра подключается к ветви с катушкой индуктивности, затем к ветви с конденсатором. В первом случае измеряется сдвиг по фазе между напряжением 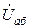и током 
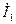, во втором – между этим же напряжением 
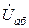и током 
).
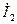4.2. Включить ГНЧ. Установить входное напряжение U (задается преподавателем).
4.3. Изменяя частоту генератора в окрестности расчетного значения резонансной частоты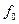 
, найти опытное значение резонансной частоты по нулевому показанию фазометра или по минимуму тока I в неразветвленной части цепи.
4.4. При изменении частоты от резонансной 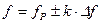, где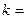 
0, 1, 2, 3, 4, 5, 
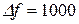Гц, в пределах 
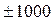Гц снять частотные характеристики 
, 
, 
.
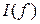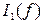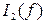4.5. На резонансной частоте определить сдвиг по фазе между напряжением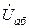 
и токами , .
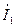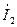4.6. Экспериментальные данные п.п. 3. занести в табл. 1. Построить графики зависимостей (опытные и расчетные)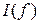 
, 
, 
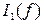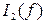и сравнить их.
4.7. Построить векторную диаграмму для токов ,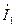 
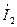и напряжения 
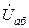на комплексной плоскости. Начальную фазу напряжения 
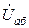принять равной нулю.
5. Контрольные вопросы
5.1. Запишите условие резонанса токов для идеального и реального параллельного контура.
5.2. Приведите формулы, по которым можно рассчитать активную, реактивную и полную проводимости параллельного контура на любой частоте, рис. 1.
5.3. Каким образом можно экспериментально изменить резонансную частоту?
5.4. Какими способами можно определить добротность параллельного RLC - контура?
5.5. Почему входное сопротивление идеального контура бесконечно большое?
5.6. Построить векторную диаграмму токов и напряжений для идеального и реального контуров.
Лабораторная работа №5
Переходные процессы в линейных электрических цепях с последовательным соединением R , L и R , C .
Цель работы
Исследование переходных процессов в простейших линейных электрических цепях при включении их под действие источников постоянного напряжения, а также переходных процессов возникающих при замыкании этих цепей.
2. Краткая теория
Переходный процесс, протекающий при включении R , L - цепи к источнику постоянной ЭДС Е (рис. 1) (ключ K мгновенно переключается из положения 2 в положение 1), описывается линейным, неоднородным дифференциальным уравнением первого порядка, составленным по второму закону Кирхгофа
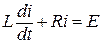, (1)
где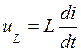 
- напряжение самоиндукции, возникающее на катушке индуктивности L при изменении тока в ней.
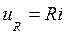- напряжение на активном сопротивление R.
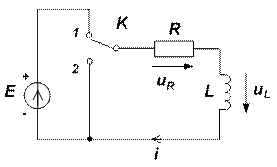
Рис. 1 Рис. 2
Решением этого дифференциального уравнения является следующая искомая функция, описывающая характер изменения тока во времени
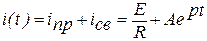, (1)
где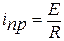 
- принужденная составляющая тока (установившееся значение тока после коммутации);
A – постоянная интегрирования;
p – корень характеристического уравнения.
Характеристическое уравнение
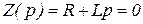, откуда 
.
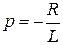Полагаем, что до коммутации ток в цепи отсутствовал, т.е. при t = 0
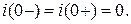
(2)
Из (1) следует, что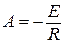 
, а решения для тока и напряжения на индуктивности принимают вид:
; 
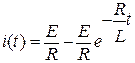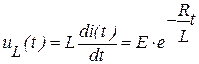. (3)
Как видно из выражения для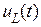 
в момент срабатывания ключа (t = 0) на катушке скачком возникает ЭДС, по величине равная напряжению E. Затем uL ( t ) постепенно уменьшается до нуля из-за уменьшения скорости нарастания тока.
Графики изменения тока и напряжения на индуктивности приведены на рис. 2.
Рассмотрим теперь, что происходит в этой цепи в дальнейшем.
При отключении катушки с током от источника E (ключ K мгновенно переключается из положения 1 в положение 2), электрическая цепь принимает вид рис. 3.
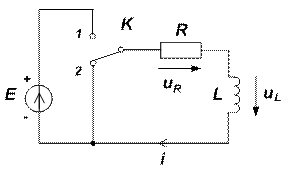
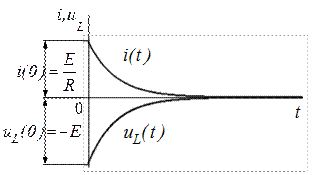
Рис. 3 Рис. 4
Переходный процесс описывается однородным дифференциальным уравнением, причем ток в момент коммутации (см. 3) на основании первого закона коммутации (ток в катушке не может измениться скачком) i (0)=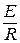 
,
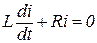, решение которого имеет вид
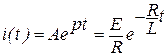, (4)
, 
.
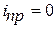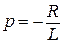Напряжение на индуктивности
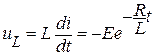. (5)
Как видно из (4) и (5) ток плавно уменьшается до нуля, а напряжение uL ( t ) скачком изменяет знак с (+) на (-). Это происходит потому, что ток в катушке не может измениться скачком и после отключения источника продолжает протекать в том же направлении, постепенно уменьшаясь по величине. При этом на катушке возникает напряжение обратной полярности, т.к. производная по току изменила свой знак. Графики изменения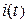 
и 
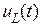приведены на рис. 4.
Скорость протекания переходного процесса характеризуется постоянной времени цепи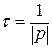 
.
Постоянная времени численно равна времени за которое исследуемая функция изменяется в е раз. При экспериментальном исследовании переходных процессов постоянная времени цепи определяется графическим путем. Так как свободная составляющая тока или напряжения описывается
уравнением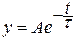 
, производная в любой точки этой кривой
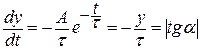, следовательно, для определения постоянной
времени в этом случае можно измерить длину подкасательной, соответствующей какому либо значению у (рис 5) и умножить её на масштаб времени.
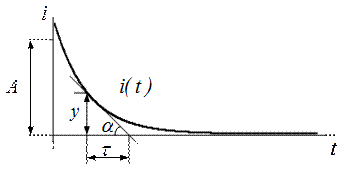
Рис. 5
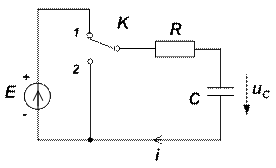
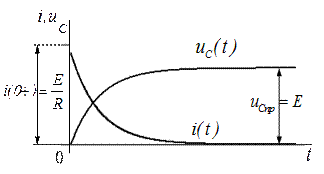
Рис. 6 Рис. 7
Рассмотрим процесс заряда конденсатора, т.е. каким образом будет нарастать с течением времени напряжение uC ( t ) (рис. 6) (ключ K мгновенно переключается из положения 2 в положение 1).
Общее решение для напряжения на емкости при решении задачи классическим методом имеет вид
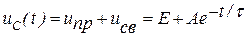. (6)
Полагаем, что до коммутации конденсатор не заряжен, т.е. при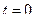 
напряжение 
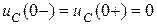, а при 
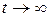конденсатор должен зарядиться до напряжения, равного E, после чего ток станет равным нулю. Из (6) следует, что 
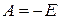, а решения для тока и напряжения принимают вид
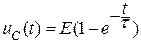и 
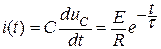. (7)
Графики изменения напряжения и тока в RC - цепи приведены на рис. 7. Они показывают, что напряжение на емкости не устанавливается мгновенно, а плавно изменяется по экспоненциальному закону от нуля до установившейся величины, равной Е; а ток в момент коммутации возрастает скачком до величины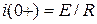 
и затем плавно по экспоненциальному закону уменьшается до нуля.
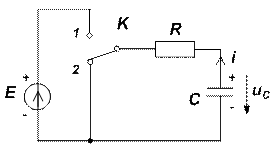
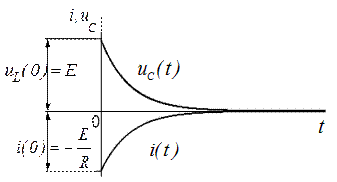
Рис. 8 Рис. 9
Если теперь мгновенно отключить источник E и мгновенно подключить к конденсатору сопротивление R, то начнется процесс разряда конденсатора. К этому моменту времени конденсатор зарядился до напряжения источника E, т.е. началом нового отсчета времени считаем uC (0+) = E. Тогда дифференциальное уравнение имеет вид
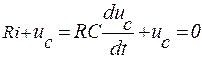(8)
Принужденная составляющая uCпр = 0 и решение уравнения 8 имеет вид uC ( t ) = Aept. Так как uC (0-) = uC (0+) = E,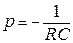 
, 
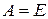, то
, 
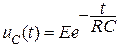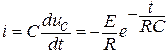(9)
Графики изменения uC ( t ) и i ( t ) приведены на рисунке 9.
Дата: 2018-11-18, просмотров: 504.
