Переходный процесс, протекающий при включении RLC-цепи к источнику постоянного напряжения Е (рис. 1), описывается линейным неоднородным дифференциальным уравнением второго порядка, составленным по второму закону Кирхгофа
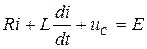, где 
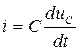. (1)
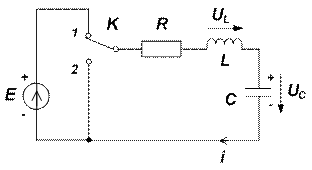
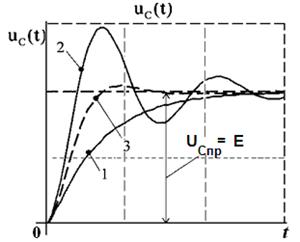
Рис. 1 Рис. 2
Объединив два соотношения в (1), получим неоднородное дифференциальное уравнение второго порядка для напряжения на ёмкости
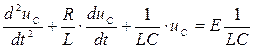. (2)
Для решения (2) составим характеристическое уравнение. Для чего в нём заменяется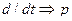 
, а правую составляющую уравнения примем равной нулю
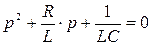. (3)
Характер свободной составляющей переходного процесса для всех токов и напряжений одной и той же цепи одинаков, зависит только от параметров R, L и C определяется корнями характеристического уравнения 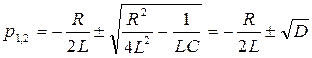(4):
. (4)
В зависимости от знака подкоренного выражения D решение для свободной составляющей напряжения на емкости имеет три вида:
1. 
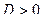, два действительных отрицательных корня - р1 и р2, процесс апериодический
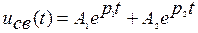; (5)
2. 
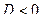, два комплексно сопряженных корня 
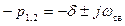, процесс колебательный
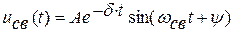; (6)
3. 
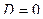, два равных действительных отрицательных корня 
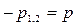, процесс критический
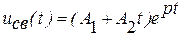. (7)
В (5)…(7) 
, 
, 
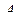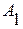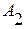и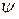 
- постоянные интегрирования, 
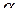- коэффициент затухания колебательного процесса, 
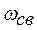- частота собственных затухающих или свободных колебаний цепи.
Для исследуемой схемы можно найти из (4) значение сопротивления R, при котором значение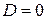 
. Такое сопротивление называется критическим Rкр и определяется выражением
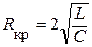. (8)
Для колебательного процесса коэффициенты 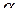и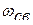 
связаны между собой, а также с параметрами цепи следующими соотношениями:
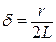; (9)
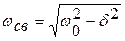, (10)
где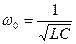 
- резонансная угловая частота последовательного колебательного контура.
Постоянные интегрирования определяются из начальных условий для искомого тока или напряжения. Так, для напряжения на емкости в колебательном режиме получаем систему из двух уравнений:
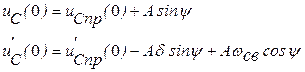. (11)
Положим, что к моменту подключения напряжения Е в схеме (рис. 1) нулевые начальные условия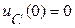 
и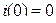 
. Для определения начального значения производной напряжения записывается уравнение по второму закону Кирхгофа для момента времени 
:
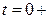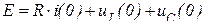(12)
Из (12) следует, что
; 
;
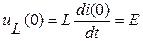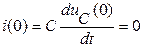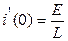и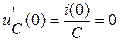 
.
Подставив начальные значения в систему уравнений (11) и с учетом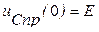 
, 
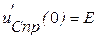, получим постоянные интегрирования А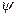 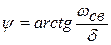и 
и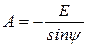 
. (13)
На рис. 2…4 изображены графики переходных процессов для напряжения на ёмкости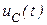 
, напряжения на индуктивности 
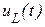и тока в цепи 
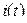, где кривые 1 соответствуют апериодическому переходному процессу, кривые 2 соответствуют колебательному переходному процессу, кривые 3 соответствуют критическому переходному процессу. Эти кривые соответственно возникают при переключении ключа K из положения 2 в положение 1.
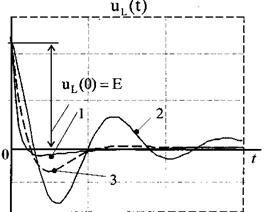
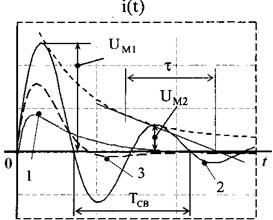
Рис. 3 Рис. 4
На рис. 4. проведены графики тока в цепи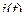 
и показано как по графику, соответствующему колебательному процессу (кривая 2), можно определить составляющие корней характеристического уравнения: коэффициент затухания 
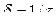, где 
- постоянная времени, равная длине подкасательной к огибающей кривой свободных колебаний; частота свободных затухающих колебаний тока или напряжения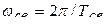 
, где Тсв - период колебаний. Для оценки скорости затухания процесса вводится декремент колебания 
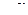, равный отношению свободной составляющей переходной величины в моменты времени, отличающиеся на период Тсв.
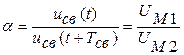(14)
При этом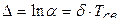 
- называется логарифмическим декрементом колебания, из чего можно определить коэффициент затухания:
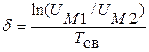. (15)
Дата: 2018-11-18, просмотров: 517.
