4.1. На лабораторном модуле собрать исследуемые электрические цепи при согласном (рис. 4), а затем при встречном (рис. 5) включении катушек.
В каждой схеме провести измерение величин, указанных в табл.1
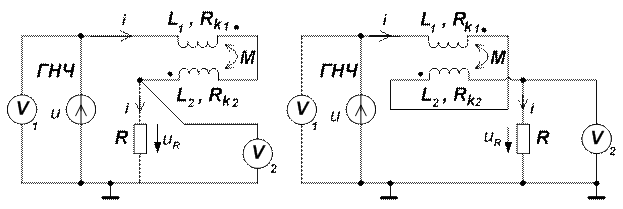
Рис. 4 Рис. 5
По результатам измерений вычислить (см. векторную диаграмму рис. 6 а, б)

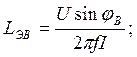
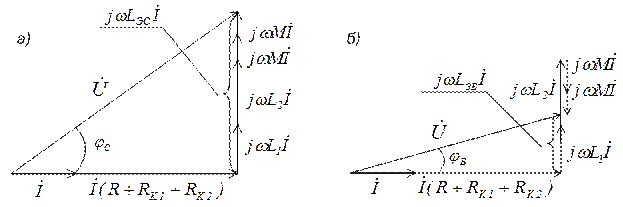
Рис. 6
4.2. В схеме (рис. 3) по результатам измерений тока в первичной обмотке и напряжения во вторичной обмотке рассчитать величину взаимной индуктивности М. Результаты расчета занести в табл.1.
5. Контрольные вопросы
5.1. Объяснить явление взаимной индуктивности.
5.2. Как записываются выражения мгновенных и комплексных значений напряжений на магнитно-связанных катушках индуктивности при заданных токах и разметке одноимённых зажимов катушек?
5.3. Объяснить, что значит согласное и встречное включение двух магнитно-связанных катушек.
5.4. Как определить величину взаимной индуктивности опытным путём?
Лабораторная работа № 3
Резонанс напряжений
Цель работы
Исследование явления резонанса напряжений в R , L , C цепи.
Краткая теория
Для режима резонанса в цепи, представленной на рис. 1, характерна возможность возникновения равных по модулю и противоположных по фазе напряжений на индуктивности катушки и конденсаторе, существенно превышающих напряжение питания цепи U (отсюда название – резонанс напряжений).
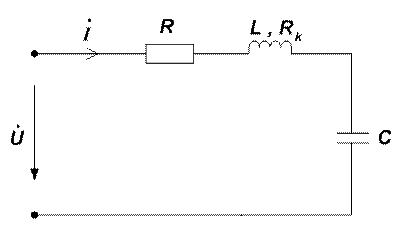
Рис. 1
Условие резонанса напряжений в последовательном контуре – равенство индуктивного сопротивления катушки XL и емкостного сопротивления конденсатора XC .
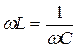 .
.
Из этого соотношения видно, что резонанса в цепи можно достичь, варьируя либо частотой приложенного напряжения, либо параметрами 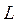 и
и 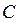 , либо тем и другим одновременно.
, либо тем и другим одновременно.
В частности, если 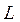 и
и 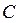 фиксированы, то для резонансной частоты получаем
фиксированы, то для резонансной частоты получаем
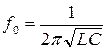 .
.
Резонансный контур характеризуется следующими параметрами:
– волновым сопротивлением 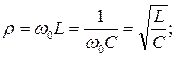
– добротностью контура 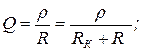
– параметром затухания 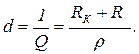
В данной работе исследование явления резонанса осуществляется изменением частоты 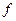 источника напряжения, и при этом рассчитываются
источника напряжения, и при этом рассчитываются
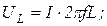
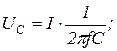
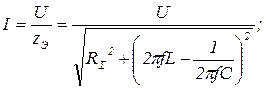
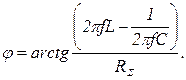
Так как при резонансе полное сопротивление минимально 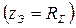 , то при постоянстве действующего значения напряжения цепи ток максимален:
, то при постоянстве действующего значения напряжения цепи ток максимален:
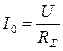 ,
,
где RΣ = R + RK .
Падение напряжения на индуктивности катушки и на емкости конденсатора при резонансе в силу равенства 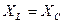 равны друг другу и сдвинуты по фазе почти на 1800 относительно друг друга, если RK << R. Частотные характеристики
равны друг другу и сдвинуты по фазе почти на 1800 относительно друг друга, если RK << R. Частотные характеристики 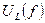 и
и 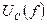 также как и
также как и 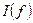 , как показано выше, имеют максимум, причем максимум
, как показано выше, имеют максимум, причем максимум 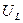 наступает при частоте
наступает при частоте
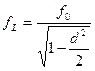 ,
,
а максимум 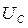 при частоте
при частоте
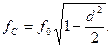
Из этих выражений видно, что с уменьшением величины RΣ или коэффициента затухания 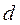 , величины
, величины 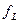 и
и 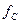 стремятся к
стремятся к 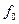 и максимумы напряжений
и максимумы напряжений  и
и 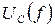 совмещаются. При возрастании RΣ, наоборот, максимумы расходятся.
совмещаются. При возрастании RΣ, наоборот, максимумы расходятся.
3. Задание для самостоятельной подготовки
3.1. По литературе [1] следует ознакомиться с разделом курса ТОЭ по резонансу напряжений.
3.2. Перечертить схему исследования (рис. 2.). Здесь емкость С = 100 нФ, сопротивление катушки R К = 27,6 Ом, индуктивность катушки 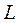 = 50 мГн, сопротивление R Ш = 10 Ом.
= 50 мГн, сопротивление R Ш = 10 Ом.
Величина напряжения источника питания ГНЧ задается преподавателем 0 < U ≤ 1 В.
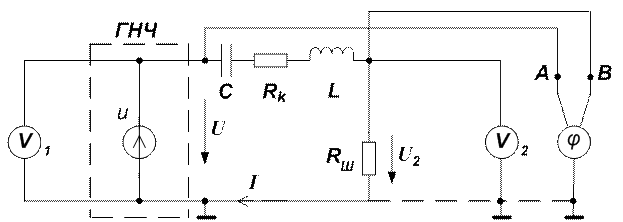
Рис 2
3.3. Используя исходные данные п.3.2 рассчитать следующие величины:
– резонансную частоту 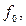 Гц;
Гц;
– волновое сопротивление 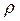 , Ом;
, Ом;
– добротность контура 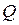 ;
;
– параметр затухания 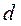 ;
;
– ток в контуре при резонансе 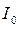 при заданном напряжении, А
при заданном напряжении, А
– напряжение на реактивной катушке и конденсаторе при резонансе, В
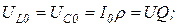
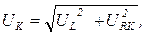 где
где 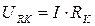 .
.
3.4. Рассчитать и построить графики зависимости 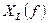 ;
; 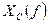 ;
; 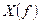 и
и 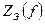 при изменении частоты от резонансной
при изменении частоты от резонансной 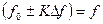 через интервалы
через интервалы 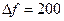 Гц в пределах
Гц в пределах
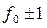 кГц (где
кГц (где 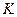 =0, 1, 2, 3, 4, 5).
=0, 1, 2, 3, 4, 5).
3.5. Рассчитать и построить графики зависимостей 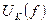 ;
; 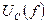 ;
; 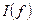 и
и 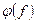 при тех же значениях частоты.
при тех же значениях частоты.
3.6. Расчетные данные п.п. 4 и 5 занести в табл. 1.
Таблица 1
| Час тота, Гц. | Опыт | Расчет | ||||||||||
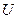 ,
В ,
В
| 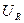 ,
В ,
В
| 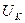 ,
В ,
В
| 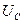 ,
В ,
В
| 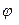 ,
град ,
град
| 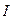 ,
А ,
А
| 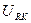 ,
В ,
В
| 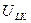 ,
В ,
В
| 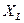 ,
Ом ,
Ом
| 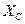 ,
Ом ,
Ом
| 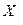 ,
Ом ,
Ом
| 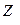 ,
Ом ,
Ом
| |
Дата: 2018-11-18, просмотров: 784.