Для заданных двух балок (рисунок 2.20) требуется:
1) записать уравнения для вычисления поперечной силы Q и изгибающего момента М на каждом участке балок в общем виде и построить эпюры Q и М;
2) для балки (схема «а») рассчитать диаметр круглого поперечного сечения, если материал балки древесина с [σ] = 10 МПа;
3) для балки (схема «б») подобрать поперечное сечение в двух вариантах: двутавровое и прямоугольное с соотношением сторон  h / b = 2, приняв материал балки сталь Ст3 с [σ] = 160 МПа;
h / b = 2, приняв материал балки сталь Ст3 с [σ] = 160 МПа;
4) для балки (схема «б») определить, какое из подобранных сечений более рационально по расходу материала.
Данные взять из таблицы 2.12
Пояснения к решению задачи 3
Решение задачи следует начинать с определения опорных реакций.
Поперечная сила и изгибающий момент определяются методом сечений. Расстояние от конца балки до выбранного сечения задается координатой x.
Величина поперечной силы Qх в любом сечении балки равна сумме проекций всех внешних сил, действующих на балку по одну сторону от рассматриваемого сечения на вертикальную ось (главную центральную ось инерции сечения).
Величина изгибающего момента Мх в любом сечении балки равна сумме моментов всех внешних сил, действующих на балку по одну сторону от рассматриваемого сечения, относительно горизонтальной оси (главной центральной оси инерции сечения).
Если внешняя сила расположена слева от сечения и направлена вверх или справа от сечения и направлена вниз, то при определении Qх она берется с положительным знаком.
Таблица 2.12
| Номер варианта | Схема по рисунку 2.20 | а, м | b, м | c, м | d, м | М, кНм | F, кН | q, кН/м |
| 1 | 1 | 1,1 | 2,1 | 0,1 | 2,0 | 10 | 10 | 10 |
| 2 | 1 | 1,2 | 2,2 | 0,2 | 1,9 | 20 | 20 | 20 |
| 3 | 1 | 1,3 | 2,3 | 0,3 | 1,8 | 3 | 3 | 3 |
| 4 | 2 | 1,4 | 2,4 | 0,4 | 1,7 | 4 | 4 | 4 |
| 5 | 2 | 1,5 | 2,5 | 0,5 | 1,6 | 5 | 5 | 5 |
| 6 | 2 | 1,6 | 2,6 | 0,6 | 1,5 | 6 | 6 | 6 |
| 7 | 3 | 1,7 | 2,7 | 0,7 | 1,4 | 7 | 7 | 7 |
| 8 | 3 | 1,8 | 2,8 | 0,8 | 1,3 | 8 | 8 | 8 |
| 9 | 3 | 1,9 | 2,9 | 0,9 | 1,2 | 9 | 9 | 9 |
| 10 | 4 | 2,0 | 3,0 | 1,0 | 1,1 | 10 | 10 | 10 |
| 11 | 4 | 1,1 | 2,1 | 0,1 | 2,0 | 10 | 10 | 10 |
| 12 | 4 | 1,2 | 2,2 | 0,2 | 1,9 | 20 | 20 | 20 |
| 13 | 5 | 1,3 | 2,3 | 0,3 | 1,8 | 3 | 3 | 3 |
| 14 | 5 | 1,4 | 2,4 | 0,4 | 1,7 | 4 | 4 | 4 |
| 15 | 5 | 1,5 | 2,5 | 0,5 | 1,6 | 5 | 5 | 5 |
| 16 | 6 | 1,6 | 2,6 | 0,6 | 1,5 | 6 | 6 | 6 |
| 17 | 6 | 1,7 | 2,7 | 0,7 | 1,4 | 7 | 7 | 7 |
| 18 | 6 | 1,8 | 2,8 | 0,8 | 1,3 | 8 | 8 | 8 |
| 19 | 7 | 1,9 | 2,9 | 0,9 | 1,2 | 9 | 9 | 9 |
| 20 | 7 | 2,0 | 3,0 | 1,0 | 1,1 | 10 | 10 | 10 |
| 21 | 7 | 1,1 | 2,1 | 0,1 | 2,0 | 10 | 10 | 10 |
| 22 | 8 | 1,2 | 2,2 | 0,2 | 1,9 | 20 | 20 | 20 |
| 23 | 8 | 1,3 | 2,3 | 0,3 | 1,8 | 3 | 3 | 3 |
| 24 | 8 | 1,4 | 2,4 | 0,4 | 1,7 | 4 | 4 | 4 |
| 25 | 9 | 1,5 | 2,5 | 0,5 | 1,6 | 5 | 5 | 5 |
| 26 | 9 | 1,6 | 2,6 | 0,6 | 1,5 | 6 | 6 | 6 |
| 27 | 9 | 1,7 | 2,7 | 0,7 | 1,4 | 7 | 7 | 7 |
| 28 | 10 | 1,8 | 2,8 | 0,8 | 1,3 | 8 | 8 | 8 |
| 29 | 10 | 1,9 | 2,9 | 0,9 | 1,2 | 9 | 9 | 9 |
| 30 | 10 | 2,0 | 3,0 | 1,0 | 1,1 | 10 | 10 | 10 |

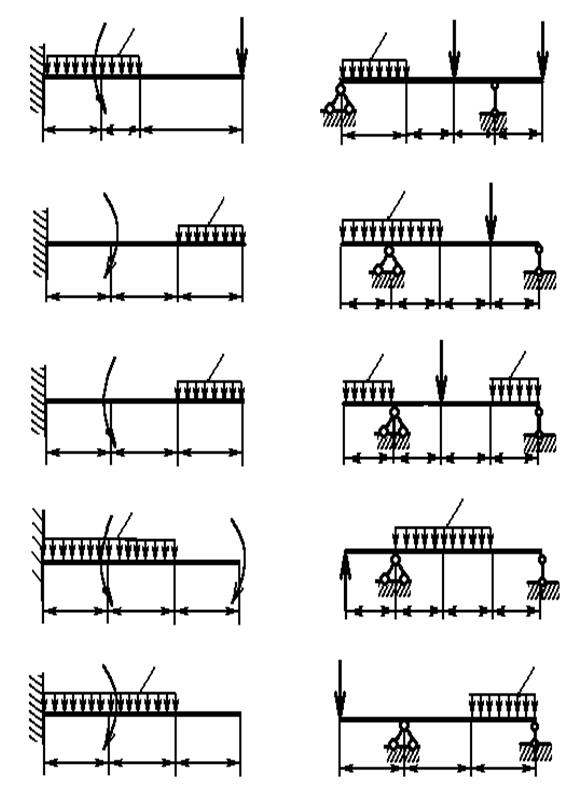
Рисунок 2.20

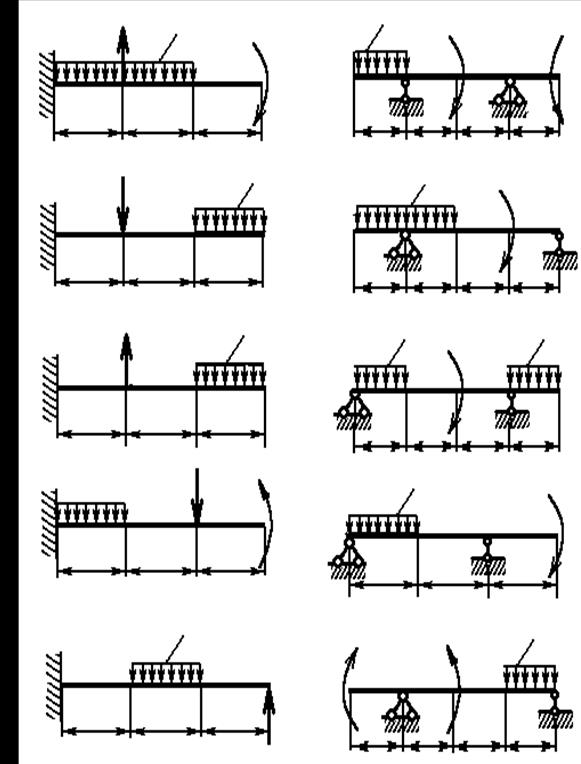
Окончание рисунка 2.20
Если внешняя сила или сосредоточенный момент расположены слева от сечения и стремятся изогнуть балку выпуклостью вниз или расположены справа от сечения и также стремятся изогнуть балку выпуклостью вниз, изгибающий момент Мх записывается с положительным знаком.
При построении эпюр балку разбивают на участки, в пределах которых Qх и Мх изменяются по одному закону (границами участков служат точки приложения сил, моментов, а также начало или конец участка с распределенной нагрузкой). На каждом участке проводят сечение на расстоянии х от начала координат и составляют аналитические выражения для Q(х) и М(х): (Q(х) = f1(х) и М(х)= f2(х)). Ось x направляют вдоль продольной оси балки, а оси y, z – вертикально и горизонтально по поперечному сечению балки. Начало координат можно располагать на любом конце балки. Для проверки правильности построения эпюр надо обратить внимание на следующее:
1) на тех участках балки, где отсутствует распределенная нагрузка, эпюра поперечных сил изобразится прямой, параллельной продольной оси балки, а эпюра изгибающих моментов – наклонной прямой;
2) на участках балки, где действует сплошная равномерно распределенная нагрузка, эпюра поперечных сил изобразится наклонной прямой, а эпюра изгибающих моментов – параболой. При этом парабола обращена выпуклостью навстречу направлению действия распределенной нагрузки. Если наклонная линия на эпюре поперечных сил проходит через ноль, парабола в этих сечениях будет иметь экстремум, значение которого надо определить;
3) в сечениях, где приложена внешняя сосредоточенная сила, на эпюре поперечных сил будет «скачок» на величину этой силы, а на эпюре изгибающих моментов – «излом»;
4) в сечениях, где действует сосредоточенный внешний момент, на эпюре изгибающих моментов будет «скачок» на величину этого момента.
Нормальное напряжение в произвольной точке поперечного сечения балки при изгибе определяют по формуле
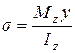
где М z – изгибающий момент в рассматриваемом поперечном сечении, Нм; Iz – осевой момент инерции площади этого сечения относительно нейтральной оси, м4; у – расстояние от нейтральной оси до рассматриваемой точки сечения, м.
Наибольшие нормальные напряжения в поперечном сечении балки возникают в точках, наиболее удаленных от нейтральной оси (горизонтальной главной центральной оси инерции сечения). Их определяют по формуле
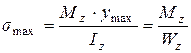 ,
,
где y 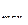 – расстояние от нейтральной оси до наиболее удаленных растянутых или сжатых волокон, м;
– расстояние от нейтральной оси до наиболее удаленных растянутых или сжатых волокон, м; 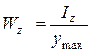 – осевой момент сопротивления поперечного сечения балки, м3.
– осевой момент сопротивления поперечного сечения балки, м3.
Необходимые размеры поперечного сечения балок при изгибе подбираются по максимальным нормальным напряжениям, действующим в точках, наиболее удаленных от нейтральной оси.
Для балок, материал которых одинаково сопротивляется растяжению и сжатию, т. е. когда 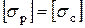 , расчетная формула на изгиб для подбора сечения записывается в следующем виде:
, расчетная формула на изгиб для подбора сечения записывается в следующем виде:
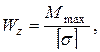
где Wz – минимальный момент сопротивления поперечного сечения балки относительно нейтральной оси, м3; Mmax – наибольший по абсолютному значению изгибающий момент, Нм; 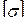 – допускаемое напряжение материала балки на изгиб, Па.
– допускаемое напряжение материала балки на изгиб, Па.
Осевые моменты сопротивления:
– круглого поперечного сечения:
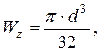
где d – диаметр сечения, м;
– прямоугольного сечения:
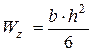 ,
,
где b и h – размеры сечения, м (в квадрат возводится размер, перпендикулярный к той оси сечения, относительно которой происходит изгиб балки).
Подбор стандартного прокатного профиля, например, двутавра, производится по таблицам в соответствии с требуемым значением Wz. Из таблицы выписывают значения ближайшего меньшего и ближайшего большего Wz стандартных профилей с указанием их номеров. Вычисляют 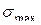 в балке с меньшим стандартным Wz и сравнивают с
в балке с меньшим стандартным Wz и сравнивают с 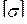 . Если при этом перегрузка балки превысит допустимую (5%), то придется использовать профиль с ближайшим большим Wz. Недогрузку балки в этом случае не рассчитывают.
. Если при этом перегрузка балки превысит допустимую (5%), то придется использовать профиль с ближайшим большим Wz. Недогрузку балки в этом случае не рассчитывают.
ЛИТЕРАТУРА
1. Винокуров А.И. Сборник задач по сопротивлению материалов. М.: Высшая школа, 1990.
2. Иосилевич Г.В. и др. Прикладная механика. М.: Высшая школа, 1989.
3. Санкович А.И. Прикладная механика. Методические указания к решению задач по одноименному курсу для студентов-заочников спец. Т 15.02, Т 16.04. Мн.: БГТУ, 1996.
4. Степин П.А. Сопротивление материалов. М.: Высшая школа, 1988.
5. Яблонский А.А. Сборник заданий для курсовых работ по теоретической механике. М.: Интеграл-Пресс, 2005
Дата: 2018-11-18, просмотров: 447.