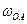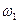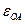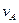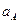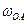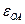Найти для заданного положения механизма скорости и ускорения точек В и С, а также угловую скорость и угловое ускорение звена, которому эти точки принадлежат.

Схемы механизмов помещены на рисунке 2.13, а необходимые для расчета данные приведены в таблице 2.9.

Таблица 2.9

Номер варианта (рисунок 2.13)	Размеры, см				рад/с	рад/с	рад/с2	см/с	см/с2
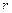
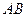
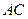
1	40	15	-	8	2	-	2	-	-
2	30	15	-	8	3	-	2	-	-
3	-	50	-	-	-	-	-	50	100
4	35	-	-	45	4	-	8	-	-
5	25	-	-	20	1	-	1	-	-
6	40	15	-	6	1	1	0	-	-
7	35	-	75	60	5	-	10	-	-
8	-	-	20	10	-	-	-	40	20
9	-	-	45	30	-	-	-	20	10
10	25	-	80	20	1	-	2	-	-
11	-	-	30	15	-	-	-	10	0
12	-	-	30	20	-	-	-	20	20
13	25	-	55	40	2	-	4	-	-
14	45	15	-	8	3	12	0	-	-
15	40	15	-	8	1	-	1	-	-
16	55	20	-	-	2	-	5	-	-
17	-	30	-	10	-	-	-	80	50
18	10	-	10	5	2	-	6	-	-
19	20	15	-	10	1	2,5	0	-	-
20	-	-	20	6	-	-	-	10	15
21	30	-	60	15	3	-	8	-	-
22	35	-	60	40	4	-	10	-	-
23	-	-	60	20	-	-	-	5	10
24	25	-	35	15	2	-	3	-	-
25	20	-	70	20	1	-	2	-	-
26	20	15	-	10	2	1,2	0	-	-
27	-	15	-	5	-	-	-	60	30
28	20	-	50	25	1	-	1	-	-
29	12	-	35	15	4	-	6	-	-
30	40	-	-	20	5	-	10	-	-

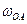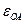Примечание.  и  - угловая скорость и угловое ускорение кривошипа  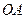при заданном положении механизма;  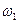- угловая скорость колеса I (постоянная);  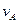и  - скорость и ускорение точки А. Качение колес происходит без скольжения.

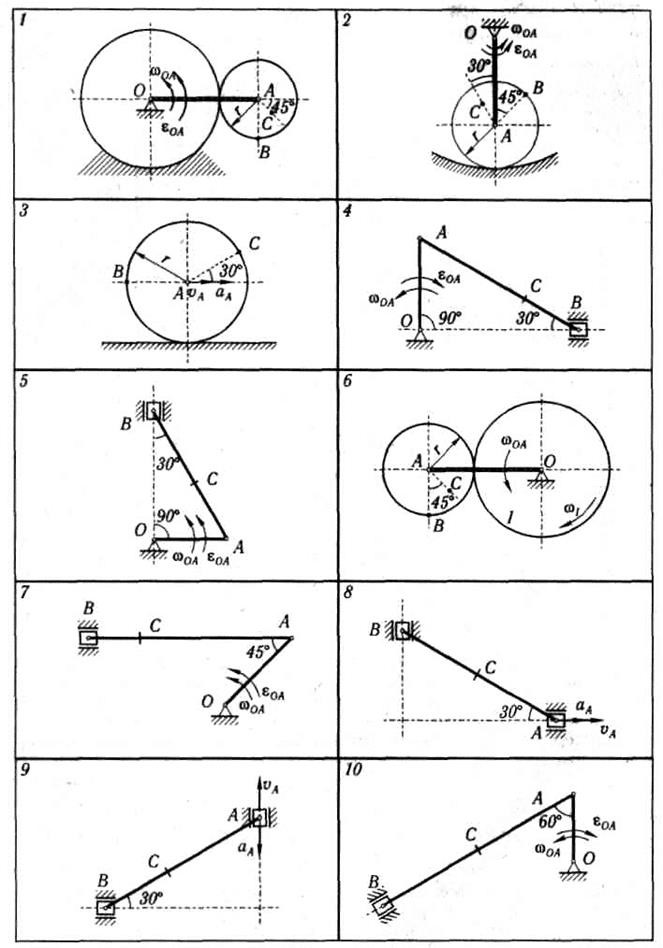
Рисунок 2.13

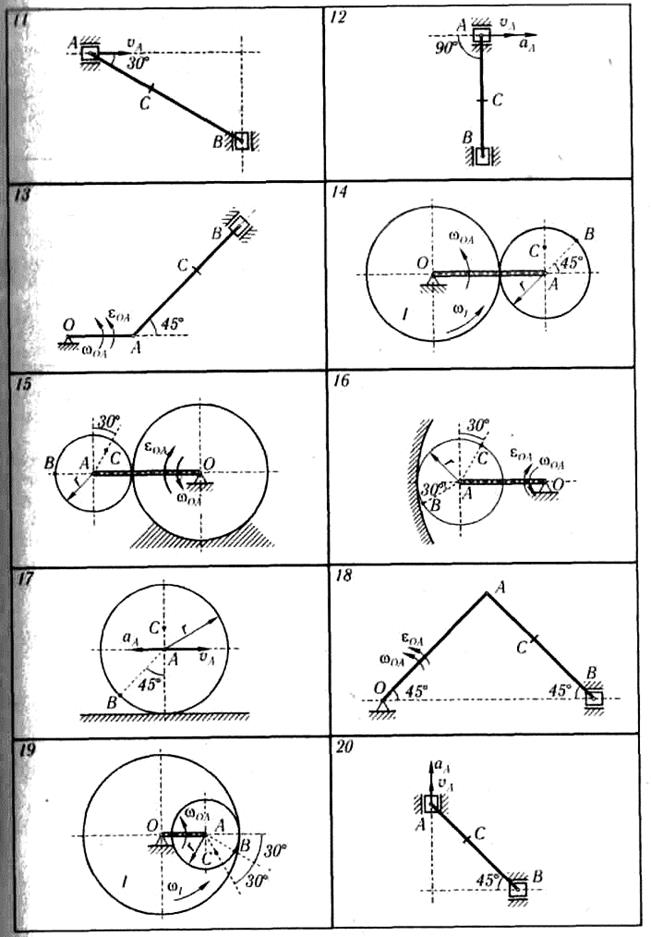
Продолжение рисунка 2.13

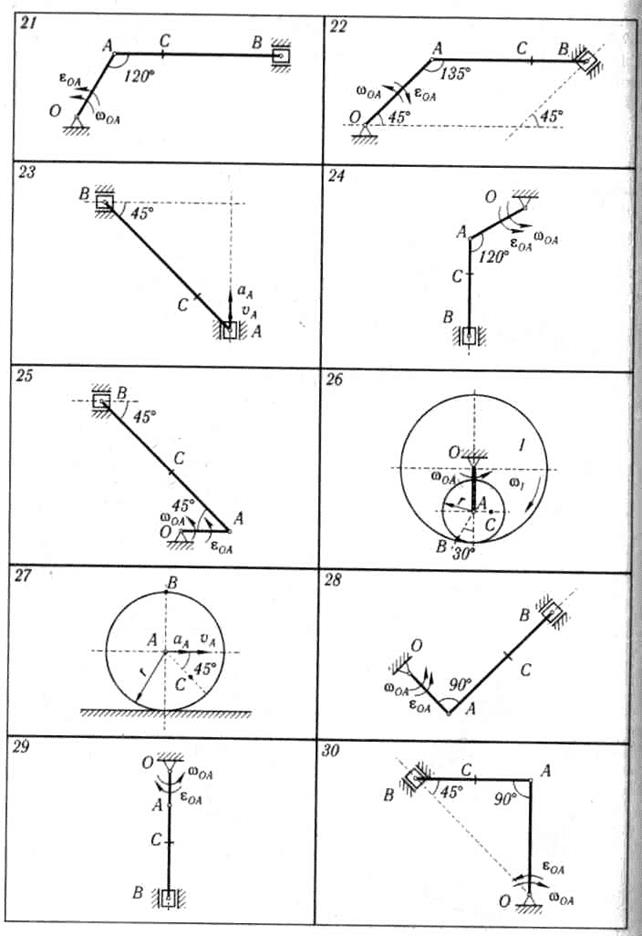
Окончание рисунка 2.13

Пример выполнения задания. Дано: схема механизма в заданном положении (рисунок 2.14); исходные данные (таблица 2.10)

Таблица 2.10

Размеры, см			рад/с	рад/с2
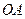
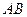
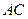
10	60	20	1,5	2

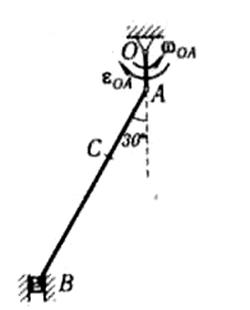
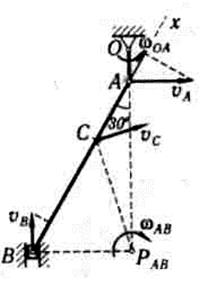
Рисунок 2.14                      Рисунок 2.15

Решение.

1. Определение скоростей точек и угловой скорости звена (рисунок 2.15). Вычисляем модуль скорости пальца А кривошипа ОА при заданном положении механизма:

.

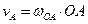Скорость точки А перпендикулярна кривошипу ОА. Скорость ползуна В направлена по вертикали. Мгновенный центр скоростей Р_АВ шатуна АВ находится в точке пересечения перпендикуляров, прове­денных из точек А к В к их скоростям.

Угловая скорость звена АВ

.

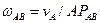Модули скорости точек В и С

;     .

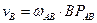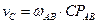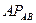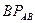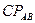Расстояния ,  и  определяются из рассмотрения треугольников  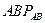и :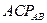

;  ;  .

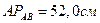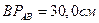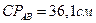В соответствии с этим ; ; ; .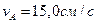

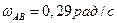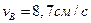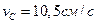Вектор 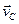 направлен перпендикулярно отрез­ку  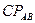в сторону, соответствующую направле­нию вращения звена АВ.

Для проверки определим скорость точки В другим способом. Воспользуемся теоремой о равенстве проекций скоростей точек на ось, прове­денную через эти точки.

Направим ось 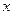 вдоль шатуна АВ в напра­влении от В к А.

Имеем 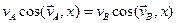, или, как видно из рисунка 2.15,

.

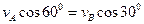Отсюда

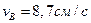
Полезно убедиться, что и найденная ранее скорость точки С удовлетворяет этой теореме.

2. Определение ускорений точек и углового ускорения звена (рисунок 2.16). Ускорение точки А складывается из вращательного и центростремительного ускорений:

;   ;   .

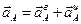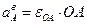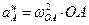Согласно теореме об ускорениях точек плоской фигуры,

,

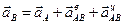или

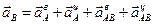.                                    (2.25)

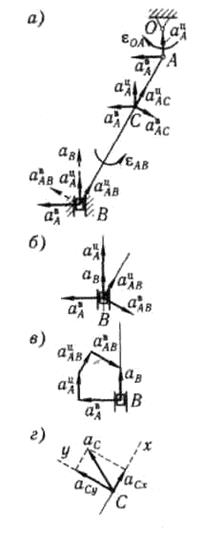
Рисунок 2.16

Центростремительное ускорение точки В во вращательном движе­нии шатуна АВ вокруг полюса А

.

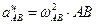По приведенным формулам вычисляем:

; ; .

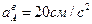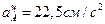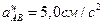Вектор 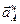 направлен от А к О. Вектор  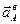перпендикулярен вектору  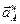и направлен противоположно  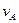(вращение кривошипа ОА — замедленное).

Вектор 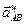 направлен от В к А. Что касается ускорения  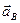точки В и вращательного ускоре­ния 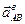, то известны только линии действия этих векторов:  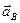— по вертикали вдоль направляю­щих ползуна,  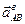— перпендикулярно АВ.

Зададимся произвольно их направлениями по указанным линиям (рисунок 2.16, в). Эти ускорения определим из уравнений проекций векторного ра­венства (2.25) на оси координат. Знак в ответе показывает, соответствует ли истинное направление вектора принятому при расчете.

Выбрав направление осей х и у, как показано на рисунке 2.16, г, получаем:

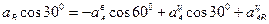;                        (2.26)

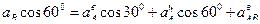.                          (2.27)

Из уравнения (2.26) находим

.

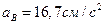Ускорение 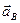 направлено, как показано на рисунке 2.16, а.

Из уравнения (2.27) получаем

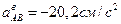
Направление 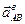 противоположно показанному на рисунке 2.16, а.

Ускорение 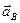 и все его составляющие с учетом их истинных направлений и масштаба показаны на рисунке 2.16, б.

Угловое ускорение шатуна АВ с учетом того, что здесь 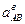 — алгебраическая величина, определяется по формуле

.

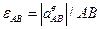Вычисляя, находим

.

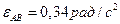Направление ускорения 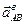 относительно полюса А определяет направление углового ускорения 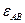. Здесь под направлением углового ускорения понимается направление дуговой стрелки, которое при ускоренном вращений звена совпадает с направлением его вра­щения, а при замедленном — противоположно ему. В данном случае угловое ускорение противоположно направлению вращения шатуна. Определить  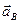и 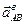 можно и графически — построением мно­гоугольника ускорений.

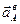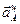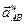Отложим из точки В согласно (2.25) в выбранном масштабе после­довательно векторы ,  и  (рисунок 2.16, в). Через конец вектора  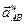проведем прямую, параллельную вращательному ускорению 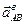, т е. перпендикулярно 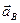, до пересечения ее с прямой, по которой направлено ускорение .

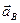Последнее определяется как замыкающая сторона многоугольника ускорений.

Модул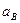и  и 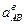 могут быть найдены измерением на чертеже.

Определяем ускорение точки С:

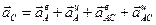
Вращательное и центростремительное ускорения точки С во вращательном движении АВ вокруг полюса А

;  ,

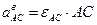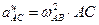или

;  .

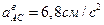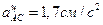Вектор 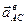 перпендикулярен вектору  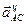и направлен соответственно угловому ускорению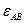

Ускорение точки С находим способом проекций (рисунок 2.16, а):

,

,

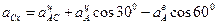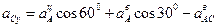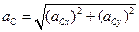
В результате вычислений получаем: 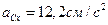; ; 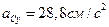 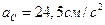(рисунок 2.16, г).