По заданным уравнениям движения точки М установить вид ее траектории и для момента времени t = t1 (с) найти положение точки на траектории, ее скорость, полное, касательное и нормальное ускорения, а также радиус кривизны траектории.
Необходимые для решения данные приведены в таблице 2.6.
Таблица 2.6
| Номер варианта | Уравнения движения | t1, с | |
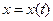 , см , см
| 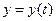 , см , см
| ||
| 1 | 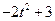
| 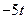
| ½ |
| 2 | 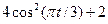
| 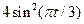
| 1 |
| 3 | 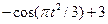
| 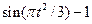
| 1 |
| 4 | 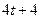
| 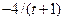
| 2 |
| 5 | 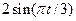
| 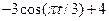
| 1 |
| 6 | 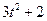
| 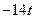
| ½ |
| 7 | 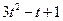
| 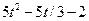
| 1 |
| 8 | 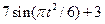
| 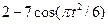
| 1 |
| 9 | 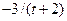
| 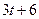
| 2 |
| 10 | 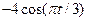
| 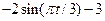
| 1 |
| 11 | 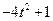
| 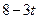
| ½ |
| 12 | 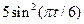
| 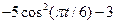
| 1 |
| 13 | 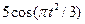
| 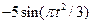
| 1 |
| 14 | 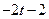
| 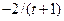
| 2 |
| 15 | 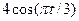
| 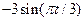
| 1 |
| 16 | 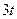
| 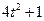
| ½ |
| 17 | 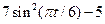
| 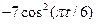
| 1 |
| 18 | 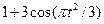
| 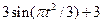
| 1 |
| 19 | 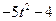
| 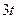
| 1 |
| 20 | 
| 
| 0 |
| 21 | 
| 
| 1 |
| 22 | 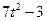
| 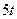
| ¼ |
| 23 | 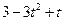
| 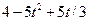
| 1 |
| 24 | 
| 
| 1 |
| 25 | 
| 
| 1 |
| 26 | 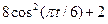
| 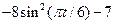
| 1 |
| 27 | 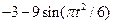
| 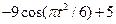
| 1 |
| 28 | 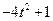
| 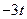
| 1 |
| 29 | 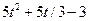
| 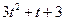
| 1 |
| 30 | 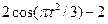
| 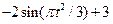
| 1 |
Пример выполнения задания. Исходные данные:
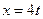 ;
; 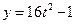 ; (2.8)
; (2.8)
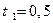 (
( 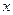 и
и 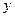 - в см,
- в см, 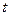 и
и 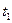 - в с).
- в с).
Решение. Уравнение (2.8) можно рассматривать как параметрические уравнения траектории точки. Чтобы получить уравнения траектории в координатной форме, исключим время 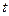 из уравнений (2.8)
из уравнений (2.8)
Получаем 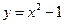 , т.е. траекторией точки является парабола, показанная на рисунке 2.10.
, т.е. траекторией точки является парабола, показанная на рисунке 2.10.
Вектор скорости точки
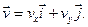 (2.9)
(2.9)
Вектор ускорения
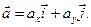
Здесь 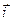 и
и 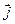 - орты осей
- орты осей 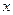 и
и 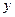 ;
; 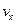 ,
, 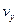 ,
, 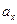 ,
, 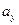 - проекции скорости и ускорения точки на оси координат.
- проекции скорости и ускорения точки на оси координат.
Найдем их, дифференцируя по времени уравнения движения (2.8):
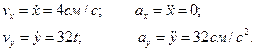 (2.10)
(2.10)
По найденным проекциям определяются модуль скорости:
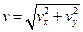 (2.11)
(2.11)
и модуль ускорения точки:
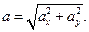 (2.12)
(2.12)
Модуль касательного ускорения точки
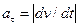 , (2.13)
, (2.13)
или
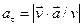 ; (2.13’)
; (2.13’)
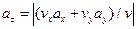 ; (2.13”)
; (2.13”)
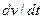 выражает проекцию ускорения точки на направление ее скорости. Знак «+» при
выражает проекцию ускорения точки на направление ее скорости. Знак «+» при 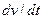 означает, что движение точки ускоренное, направления
означает, что движение точки ускоренное, направления 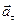 и
и 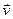 совпадают; знак «-», - что движение замедленное.
совпадают; знак «-», - что движение замедленное.
Модуль нормального ускорения точки
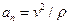 . (2.14)
. (2.14)
Если радиус кривизны траектории 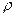 в рассматриваемой точке неизвестен, то
в рассматриваемой точке неизвестен, то 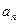 можно определить по формуле
можно определить по формуле
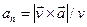 . (2.15)
. (2.15)
При движении точки в плоскости формула (2.15) примет вид
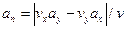 . (2.15’)
. (2.15’)
Модуль нормального ускорения можно определить и следующим образом:
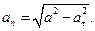 (2.16)
(2.16)
После того, как найдено нормальное ускорение по формулам (2.15) или (2.16), радиус кривизны траектории в рассматриваемой точке определяется из выражения
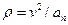 . (2.17)
. (2.17)
Результаты вычисления по формулам (2.10)-(2.13), (2.15) и (2.17) для заданного момента времени 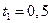 с приведены в таблице 2.7
с приведены в таблице 2.7
Таблица 2.7
| Координаты, см | Скорость, см/с | Ускорение, см/с2 | Радиус кривизны, см | |||||||
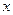
| 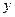
| 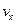
| 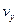
| 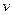
| 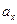
| 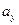
| 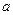
| 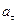
| 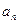
| 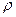
|
| 2,0 | 3,0 | 4,0 | 16,0 | 16,5 | 0 | 32,0 | 32,0 | 31,0 | 7,8 | 35,0 |
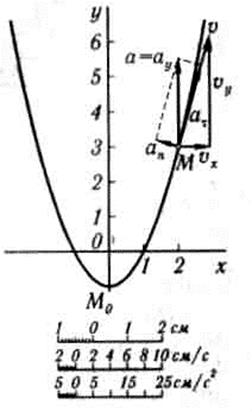
Рисунок 2.10
На рисунке 2.10 показано положение точки М в заданный момент времени. Вектор 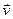 строим по составляющим
строим по составляющим 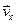 и
и 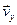 , причем этот вектор должен по направлению совпадать с касательной к траектории. Вектор
, причем этот вектор должен по направлению совпадать с касательной к траектории. Вектор 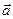 строим по составляющим
строим по составляющим 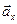 и
и 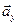 и затем раскладываем на составляющие
и затем раскладываем на составляющие 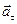 и
и 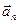 . Совпадение величин
. Совпадение величин 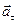 и
и 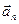 найденный из чертежа, с их значениями, полученными аналитически, служим контролем правильности решения.
найденный из чертежа, с их значениями, полученными аналитически, служим контролем правильности решения.
Дата: 2018-11-18, просмотров: 435.