Вопросы темы:
1. Умозаключения по аналогии
2. Индуктивные умозаключения
3. Силлогизм – дедуктивное умозаключение. Правила простого категорического силлогизма.
4. Фигуры и модусы простого категорического силлогизма.
5. Правила фигур.
Опосредованные умозаключения отличаются тем, что они, в отличие от непосредственных, делаются из нескольких посылок. Разница между ними определяется направлением движения нашей мысли: от частного к общему, от общего к частному, от частного к частному. В результате в мышлении сложились три схемы: индукция, дедукция, аналогия.
Самая распространенная, но и наименее надежная – аналогия. Не случайно Леонардо да Винчи предостерегал: бойтесь женщин и аналогий. Аналогия - это умозаключение, в котором от сходства предметов в одних признаках наша мысль переходит к выводу об их сходстве и в других признаках. Так мыслят дети, первобытные люди, да и все мы, когда идем по пути переноса известных нам признаков на что-то неизвестное: мой друг инженер, он образован, умен, авторитетен, интересуется живописью и имеет замечательную семью. Новый знакомый тоже инженер. Он образован и умен, пользуется авторитетом у коллег. По аналогии должен последовать вывод, что и он интересуется живописью, имеет замечательную семью. Но каждый из нас понимает, что это вовсе не обязательно. Именно поэтому выводы по аналогии носят лишь проблематичный характер. В таком простом примере вы не ошибетесь, а в более сложном? Ошибаемся, да еще как часто!
Схема аналогии такова:
А обладает признаками a, b, c, d
В обладает признаками a , b , c
Вероятно В обладает признаком d
Правило аналогии: если два единичных предмета сходны в определенных признаках, то они могут быть сходны и в других признаках, обнаруженных в одном из сравниваемых предметов.
Различают несколько видов аналогии. В зависимости от характера переносимой информации встречаются аналогия свойств (при переносе признаков с одного предмета на другой) и аналогия отношений (когда переносятся сходные отношения, а сами предметы не сравниваются). Частой ошибкой здесь бывает уподобление отношений самим предметам.
В зависимости от характера выводного знания различают строгую аналогию, предполагающую необходимую связь признаков и предметов, и нестрогую аналогию, когда связь сходных и переносимых признаков слаба.
Поскольку аналогия – весьма частая схема нашего мышления и, кроме того, именно она лежит в основе широко используемого в науке и технике метода моделирования, необходимо знать те способы, с помощью которых можно повысить достоверность получаемого вывода. Это во-первых, требование отслеживать сходство не в любых, а лишь в существенных признаках, во-вторых, необходимо, чтобы сравнение было по возможности более полным; в-третьих, признаки должны быть по возможности разнообразными; в-четвертых, перенос признаков должен быть связан с представлением о причинах сравниваемых явлений. И важно помнить, что чем меньше различий между сравниваемыми предметами, тем достовернее будут результаты аналогии.
Индукция – это схема рассуждения, в которой мысль движется от частного к общему, от знания, меньшей степени общности к знанию большей степени общности, от фактов к теории. Выводы из такого хода рассуждений носят вероятностный характер. В истории логики было разное отношение к индукции: от полного отрицания ее значимости до провозглашения основным средством познания. Истина как всегда посередине, и в конце концов индукция прочно заняла свою нишу среди схем нашего мышления, достоинства и недостатки которого необходимо знать каждому.
Прежде всего, необходимо иметь в виду, что индукция может быть полной и неполной. Полная индукция встречается редко, поскольку для нее необходимо найти некий замкнутый класс с обозримым числом элементов. Это может быть, например, студенческая группа, класс в школе, состав команды, количество учебных предметов, проходимых по программе, число предприятий в регионе, количество партий, государств, наград и т.д. случай этот не просто редкий, но малопознавательный. Не надо быть семи пядей во лбу, чтобы, просмотрев весь список и убедившись, что каждому его элементу принадлежит какой-то признак, сделать вывод о том, что этот признак принадлежит и всей группе в целом. Преимущество такого вывода состоит в том, что он носит необходимый, а не вероятностный характер. Но стоит вдруг обнаружить новый элемент рассматриваемой совокупности, который мы не заметили ранее, как вся построенная конструкция может развалиться как карточный домик. В этом случае мы будем иметь дело уже с неполной индукцией, которая встречается значительно чаще.
По способу обоснования индукция бывает популярной и научной. В первом случае достаточно простой повторяемости какого-то признака, чтобы сделать вывод. Так делались выводы о видах на урожай, такой характер носят пословицы, так рассуждают люди в обыденной жизни. Увеличить вероятность истинности в случае популярной индукции модно, если хотя бы не допускать таких ошибок, как «поспешное обобщение», когда учитываются не все обстоятельства (такой ошибкой, например, может быть доверие к слухам, сплетням), «после того, значит вследствие того», подмены условного безусловным. Причина ошибок банальна: либо мало фактов, либо они однообразны, а в результате мысль идет по самому простому и привычному пути, берется версия, «близкая сердцу», но не обязательно соответствующая действительности.
Научная индукция отличается тем, что пытается увидеть за повторяемостью причину этой повторяемости. Так открывались очень многие законы науки. Основными требованиями в данном случае являются: методичный отбор фактов, внимание к существенным признакам, раскрытие их внутренней обусловленности, сопоставление полученного вывода с уже доказанными положениями науки.
Среди методов научной индукции, т.е. методов установления причинных связей выделяют метод сходства, когда обнаруживается и исследуется общее в различном, метод различия – нахождение различного в сходном, соединенный метод сходства и различия, метод остатков.
Каждый из этих методов дополняет друг друга, но еще лучше, если индукция применяется в сочетании с дедукцией, которая позволяет исключить случайные обстоятельства.
Дедукция – логический вывод по схеме: от общего положения к частным выводам. Со времен Аристотеля первенство здесь принадлежит так называемым силлогизмам (с греческого – вычитание, сосчитывание) – умозаключениям из двух истинных простых категорических суждений, которые в результате дают новое категорическое суждение в качестве вывода.
Вывод делается на основе аксиомы простого категорического силлогизма: все, что утверждается или отрицается о роде (классе) с необходимостью утверждается (отрицается) о виде (элементе класса), принадлежащему данному роду.
Схема простого категорического силлогизма следующая: меньший термин – понятие, которой в заключении становится субъектом, больший термин – понятие, которое становится в заключении предикатом, средний термин – понятие, связывающее крайние (меньший и больший) термины, но в заключении отсутствующее. Без среднего термина крайние термины оказываются несравнимыми.
Суждение, в котором находится больший термин, называется большей посылкой. Она, как правило, формулируется раньше меньшей посылки – суждения, содержащего меньший термин.
Силлогизмы строятся в соответствии с правилами, которые делятся на правила посылок и правила терминов. Правила терминов: 1) в каждом силлогизме должно быть только три термина, иначе возникнет ошибка «учетверение терминов», которая приведет к неправильным выводам или не позволит сделать вывод вообще. Учетверение чаще всего происходит вследствие употребления омонимов, дающих возможность различного толкования исходных понятий;
2) средний термин должен быть распределен хотя бы в одной из посылок, в противном случае теряется связь между посылками;
3) термин, не распределенный в посылках, не может быть распределен в заключении.
Правила посылок:
1) хотя бы одна из посылок должна быть суждением утвердительным. Из двух отрицательных посылок вывод не следует, поскольку крайние термины у них оказываются несвязанными между собой;
2) если одна из посылок суждение отрицательное, то и вывод будет отрицательным;
3) хотя бы одна из посылок должна быть суждением общим. Из двух частных суждений дедуктивный вывод не следует;
4) если одна из посылок суждение частное, то и заключение будет частным.
Следующей характеристикой простого категорического силлогизма является его фигура или разновидность. Она определяется в зависимости от положения среднего термина в обоих посылках. Он может занимать место субъекта в большей посылке и предиката в меньшей:

 М Р
М Р
 S М
S М
Это I фигура силлогизма. Она самая распространенная и позволяет сопоставлять частное знание, выраженное в меньшей посылке с общими положениями, содержащимися в большей посылке. Именно таким образом мы строим свои рассуждения, когда нам необходимо уяснить конкретные вопросы на основе имеющегося общего правила.
У каждой фигуры есть свои правила. Правила первой фигуры таковы:
1. большая посылка должна быть суждением общим (А, Е)
2. меньшая посылка – утвердительной (А, I).
Попробуйте построить рассуждение, нарушая эти правила, и Вы придете к абсурду. Сравним умозаключение, соответствующее правилам с умозаключением, им не соответствующим:
все спортсмены – закаленные люди (большая посылка – А)
некоторые студенты – спортсмены (меньшая посылка – I )
следовательно, некоторые студенты закаленные люди
Вывод получился частным (некоторые) в соответствии с правилом посылок: если одна из посылок суждение частное, то и вывод будет частным.
А теперь нарушим правила:
все спортсмены – закаленные люди (большая посылка – А)
ни один долгожитель не является спортсменом (меньшая посылка – Е)
Следовательно, ни один долгожитель не является закаленным человеком.
Но это явная ошибка, появившаяся вследствие того, что наличие в качестве меньшей посылки суждения Е противоречит второму правилу I фигуры.
II фигура : средний термин находится на месте предиката в обеих посылках
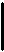
 М
М
 М
М
Такой вариант рассуждений применяется при доказательстве ложности какого-либо положения путем отрицания принадлежности предмета, о котором говорится в меньшей посылке, к тому классу, о котором говорится в большей посылке. Это фигура отрицания, поэтому и выводом из нее всегда бывает отрицательное суждение. А получается оно в соответствии с правилом посылок (если одна из посылок - суждение отрицательное, то и вывод будет отрицательным). Соответственно, правила II фигуры следующие:
1. большая посылка должна быть суждением общим (сравните с первым правилом I фигуры – они совпадают)
2. одна из посылок должна быть суждением отрицательным.
Попробуйте поиграть с нарушением этих правил и посмотрите, что у вас из этого получится.
Ну, например, сделайте вывод из двух утвердительных суждений:
Все собаки имеют уши (суждение А)
Это существо имеет уши (суждение А)
Вывод явно опрометчивый: это существо – собака, но он единственно возможный в соответствии с данным ходом рассуждений. Даже если без особых на то оснований в форме приведенных суждений принять во внимание условие, что вывод должен быть отрицательным, нам все равно не удастся избавиться от необоснованности сделанного вывода.
I и II фигуры считаются самыми распространенными и соответствующими наиболее типичным путям нашей мысли. О III и IY фигурах этого сказать нельзя, но для полноты картины они всегда рассматриваются в логике, хотя и с оговорками.
III фигура симметрична второй: средний термин находится на месте субъекта в обеих посылках.
М
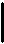

 М
М
Такой вариант рассуждений возможен, когда из двух общих положений нужно сделать вывод о том предмете, который в них обоих мыслится (то есть устанавливается совместимость понятий), или в случаях, когда мы формулируем исключения из правил.
Все дети беззащитны
Все дети шалуны
Следовательно, Некоторые шалуны беззащитны.
Такой странный вывод (из двух общих суждений вдруг получается частное) не случаен и соответствует правилу данной фигуры.
Правила III фигуры:
1. меньшая посылка должна быть утвердительной
2. заключение может быть только частным суждением
Наконец, симметричная первой, IY фигура силлогизма. Средний термин в ней занимает место предиката в большей посылке и субъекта в меньшей:

 Р М
Р М
 М S
М S
Эта фигура носит искусственный характер, но все же иногда применяется.
Правила IY фигуры:
1. если большая посылка суждение утвердительное, то меньшая должна быть общей
2. если одна из посылок суждение отрицательное, то большая должна быть общей.
3. при этом общеутвердительного вывода рассуждения по этой фигуре не дают.
Ничего не скажешь, простенькие правила! А в качестве примера можно привести следующее рассуждение:
Все инженеры – специалисты с высшим образованием
Все специалисты с высшим образованием учились в ВУЗе
Следовательно, некоторые учившиеся в ВУЗе – инженеры.
Пожалуй, каждому ясно, что так «наоборот» мы действительно никогда не рассуждаем.
Каждая фигура имеет свои разновидности в зависимости от того, какие суждения в нее входят. Это модусы. В принципе их может быть 64. Но большая их часть противоречит либо общим правилам силлогизма, либо правилам той или иной фигуры. Поэтому в конечном итоге остается всего 19 модусов: по четыре в первой и второй фигурах, шесть в третьей и пять в четвертой. Они обозначаются тремя латинскими буквами в соответствии с тем, какие именно суждения в них входят (например, АЕЕ или ОАО и т.д.).
Попробуйте самостоятельно вывести модусы каждой фигуры в тетради для самостоятельных работ, отмечая причину, по которой вы исключаете неработающие модусы.
Вопросы для закрепления материала:
1. В чем отличие непосредственных и опосредованных умозаключений?
2. Какой ход рассуждений используется в умозаключениях по аналогии?
3. Как повысить степень достоверности выводов по аналогии?
4. Чем принципиально отличаются индуктивные умозаключения от дедуктивных?
5. Какая разница между научной и популярной индукцией?
6. Если нам известен полный состав группы, о которой необходимо сделать индуктивный вывод, каким он окажется, достоверным или вероятностным?
7. Что означает понятие «силлогизм»?
8. Какие суждения входят в состав простого категорического силлогизма?
9. Попытайтесь объяснить с помощью кругов Эйлера, почему из двух отрицательных посылок нельзя сделать дедуктивный вывод?
10. Чем обусловлена ошибка «учетверение терминов»?
11. Почему из двух частных суждений нельзя сделать вывод по дедуктивной схеме?
12. Почему недопустим модус ЕЕЕ?
13. В чем причина, по которой модус АЕЕ исключается из модусов первой фигуры?
Литература
Берков В.Ф., Яскевич Я.С., Павлюкевич В.И. Логика. Минск.1997.
Гетманова А.Д Логика. Учебник для педагогических институтов. М. 1997.
Демидов И.В. Учебное пособие по логике. М.2000.
Ивин А.А. Искусство правильно мыслить. М.1966.
Ивин А.А. Практическая логика. М.1996.
Ивин А.А. Логика. Учебное пособие. М.1998.
ИвлевЮ.В. Логика. М.1992.
Кириллов В.И., Старченко А.А. Логика. М.1999.
Курбатов В.И. Логика. Систематический курс. Ростов-наДону. 2001.
Никифоров А. Книга о логике. М. Рус.феноменол.об-во «Гнозис». 1999.
Яшин Б.Л. Задачи и упражнения по логике. М.1996.
Дата: 2018-11-18, просмотров: 670.