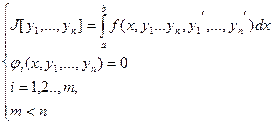
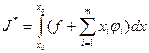
(1)
(2)
(3)
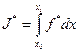
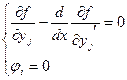
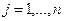
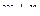 уравнений
уравнений
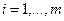
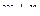 неизвестных
неизвестных
Теорема
Функции 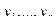 , реализующие экстремум формулы (1) при наличии условий (2) удовлетворяют (при соответствующем выборе
, реализующие экстремум формулы (1) при наличии условий (2) удовлетворяют (при соответствующем выборе 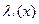 ) уравнению Эйлера, составленному для функционала (3)
) уравнению Эйлера, составленному для функционала (3)
Пример 1:
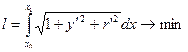
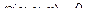
Найти кратчайшее расстояние на поверхности
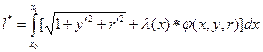
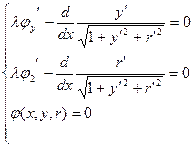
Пример 2:
Механическая система:
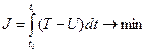
U – потенциальное поле
Связи: 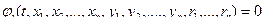


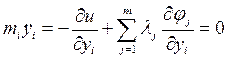
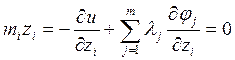
Изопериметрические задачи
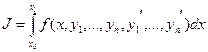

 ,
, 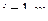
Введем новые переменные
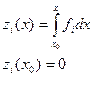
тогда 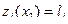
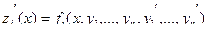


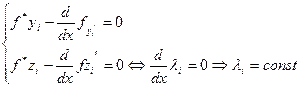
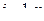 ,
, 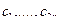 ,
, 
Неизвестные: 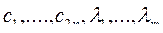
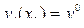 ,
, 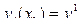 2n условий
2n условий
 m условий
m условий
Принцип взаимности
Уравнения Эйлера не изменятся, если 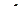 умножить на
умножить на 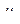
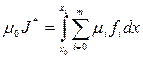 ,
, 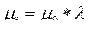
Теперь все 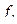 i=0,n входят в
i=0,n входят в 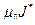 симметрично, поэтому экстремум в исходной задаче и следующей задаче совпадают
симметрично, поэтому экстремум в исходной задаче и следующей задаче совпадают
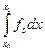
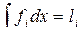 ,
, 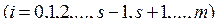
Пример 1
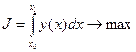
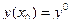 ,
, 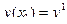
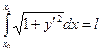 - изопериметрическое условие
- изопериметрическое условие
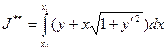
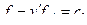 - первый интеграл
- первый интеграл
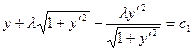
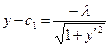 , полагая
, полагая 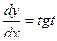 ,
, 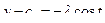
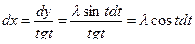

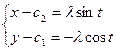

Пример 2
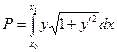 - статический момент относительно ОХ
- статический момент относительно ОХ
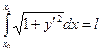
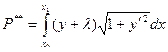
первый интеграл
 ,
, 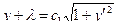
 ,
, 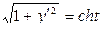
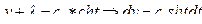
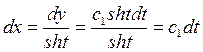
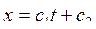 ,
, 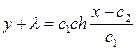

Геодезические экстремали
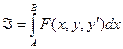 - есть
- есть 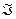 -длина кривой y(x).
-длина кривой y(x).
Если y(x) – экстремаль, то 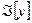 - геодезическое расстояние
- геодезическое расстояние
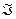 - окружность (геодезическая окружность)
- окружность (геодезическая окружность)
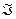 - эллипс,
- эллипс, 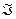 - гипербола
- гипербола
Пример:
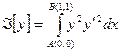
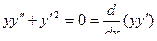
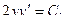
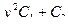
 ;
; 
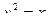
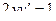
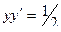

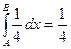 -
- 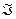 -длина
-длина
Пример:
Найти 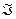 - окружность в
- окружность в 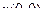 радиусе R
радиусе R
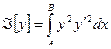
Из предыдущего:
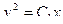
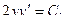

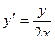
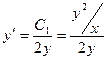
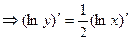
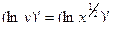



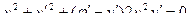

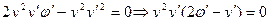
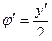

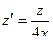
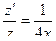
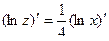
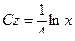
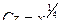
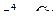
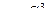

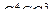
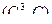 - лежит на окружности и на экстремали
- лежит на окружности и на экстремали
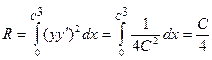

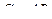
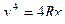
Пусть поверхность задана векторным уравнением

Геодезической линией называется линия наименьшей длины соединяющей две точки на поверхности.
Линия на поверхности

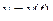
Её длина
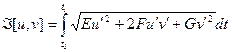
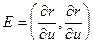
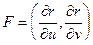

Уравнение Эйлера
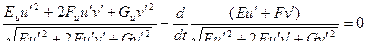
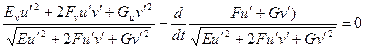
Пример:
Среди всех кривых на сфере R соединяющих две точки выделить те, которые имеют наименьшую длину.
 -долгота
-долгота 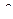 -широта
-широта

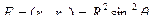

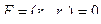
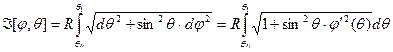
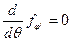
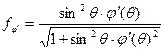

Объекты управления
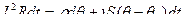
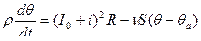



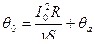
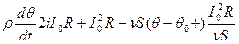 =
= 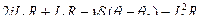
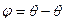
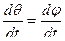
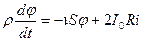
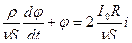

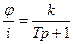
Уровень в бане
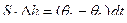

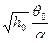
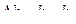

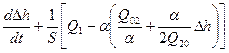 =
= 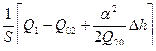

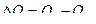
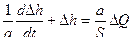
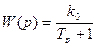
Преобразования Лапласа
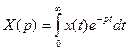
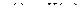
Регуляторы
П – пропорц.
ПИ – пропорц-интегр.
ПИД – пропорц-интегр-дифференц.


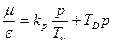
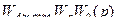
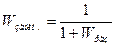
Вывод.
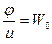
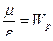
 =
= 
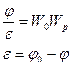


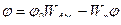

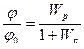
Задача: выбрать параметры 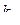 ,
, 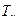 ,
, 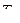 , чтобы обеспечить устойчивость и качество регулирования (переходного процесса).
, чтобы обеспечить устойчивость и качество регулирования (переходного процесса).

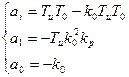
Критерий Рауса-Гурвица
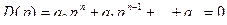

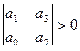
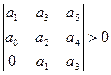 …
…
необх. и дост.. чтобы все определители имели знаки одинаковые со знаком первого коэффициента k-го уравнения.
Частотный критерий
Михайлов
Найквист
Если разомкнутая система является неустойчивой, то для того чтобы замкнутая система была устойчивой необходимо и достаточно, чтобы амплитудно-фазовые характеристики разомкнутой системы  при изменении
при изменении  от 0 до
от 0 до 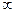 , охватывали точку
, охватывали точку 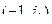 в положительном направлении
в положительном направлении 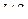 раз, где l число кривых k-го уравнения разомкнутой системы.
раз, где l число кривых k-го уравнения разомкнутой системы.
Михайлов
Для ого чтобы (замкнутая) система была устойчивой необх. и. дост. чтобы кривая Михайлова (гедограф) при изменении  от 0 до
от 0 до 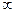 начинался
начинался 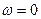 на вещественной положительной полуоси обходящей только против часовой стрелки последующие n-квадрантов n-порядок k-го уравнения.
на вещественной положительной полуоси обходящей только против часовой стрелки последующие n-квадрантов n-порядок k-го уравнения.
Постановка задачи оптимального управления
































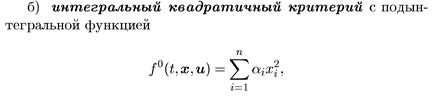

























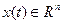
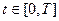
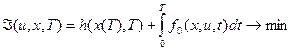

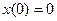
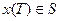
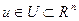
Множество конечных состояний S задается

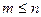

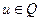
 - непрерывны по переменным x и y
- непрерывны по переменным x и y
Примеры объектов управления
Бак
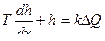
 ,
, 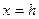
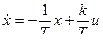
Печь нагревания

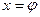 ,
, 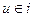
Управление космическим аппаратом



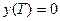
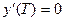
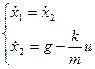

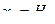
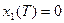


а) 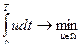
b) 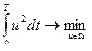
Пример:
 ;
;
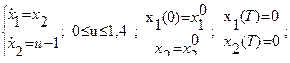
 ;
;
 ;
;
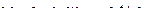 ;
;
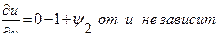
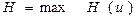

 ;
;
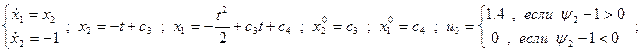
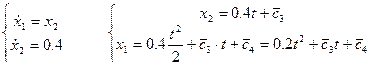 ;
;
Пример1:
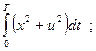
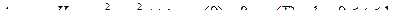
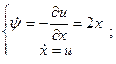
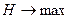 ;
;
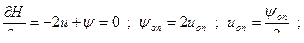


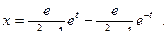
Пример 2:



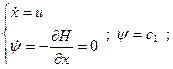
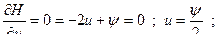
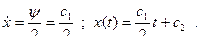
Доказательство принципа максимума
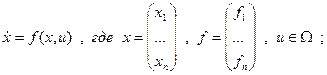
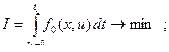

Сведём задачу к задаче … :
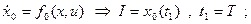
Перепишем задачу:
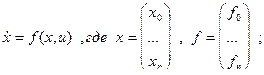
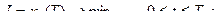

Найти xоп – оптимальный, uоп – оптимальный. Пусть 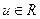 п – скалярное управление.
п – скалярное управление.
Допустим, что xоп и uоп найдены. Проварьируем управление на малом промежутке ε, изменив управление до величины u ≠ uоп ( игольчатая вариация ).
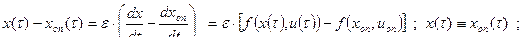
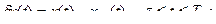
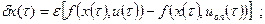
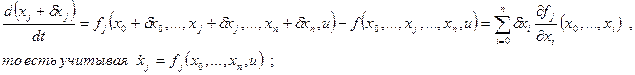
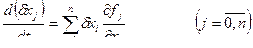

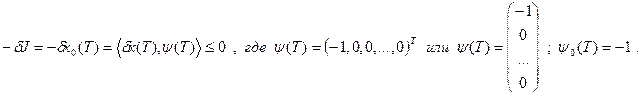
Поставим задачу получить ψ(T), который удовлетворил бы уравнению:
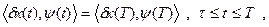
в частности, 
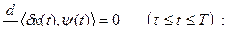
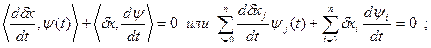
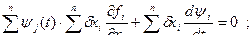
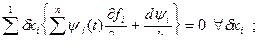
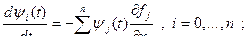


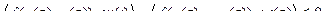
Обозначим 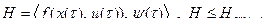
Отсюда следует, что Н достигает максимума при оптимальном 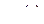 ,следовательно, надо выбирать
,следовательно, надо выбирать 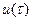 так, чтобы Н достигала максимального значения.
так, чтобы Н достигала максимального значения.
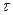 – произвольно ,
– произвольно , 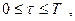 при n максимальном.
при n максимальном.
Численный метод решения задач оптимального управления.
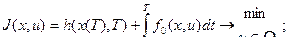
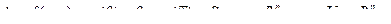
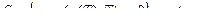
Краевая задача
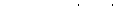
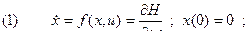
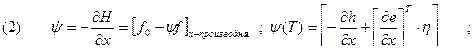

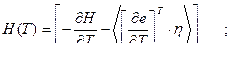

Метод стрельбы
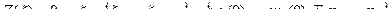 .
.
Задача Коши
Интегрируя (1) и (2) с некоторыми значениями  находят
находят 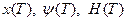 и определяют
и определяют 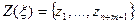 , где
, где
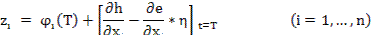
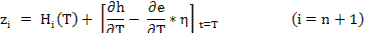
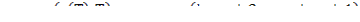
Численно используется метод Ньютона:
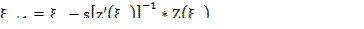
Или регуляризованный алгоритм:
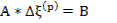

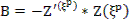
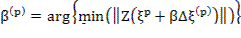

Z’ – матрица;
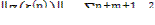 - сумма невязок
- сумма невязок
α – параметр регуляризации;
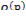 –параметр шага;
–параметр шага;
T – транспонированная матрица, Е – единичная матрица.
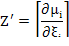
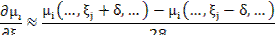
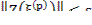
Задача о подъеме ракеты зонда
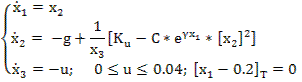
x1 – высота; х2 – скорость; х3 – переменная масса; К – коэффициент, характеризующий силу тяги;
g, c, γ – ускорение свободного падения, коэффициент аэродинамики сопротивления, коэффициент убывания плотности.
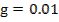 ;
; 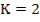 ;
; 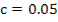 ;
; 
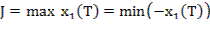
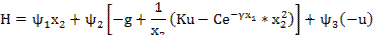
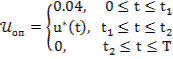 – скользящий равен
– скользящий равен 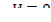
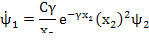
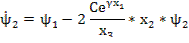
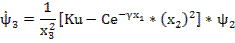
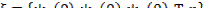
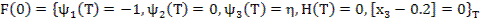
Задача о манёвре самолёта
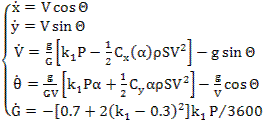 0.05
0.05 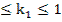
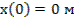
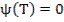

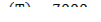

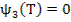
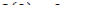
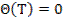
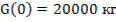
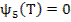
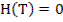
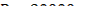 ;
;
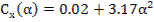 ;
;
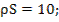
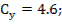
Метод решения:
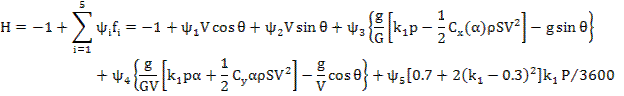
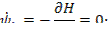
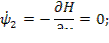

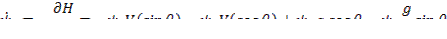
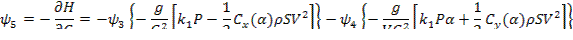
Задача о перелёте с орбиты Земли на орбиту Марса.
Задача 11.
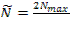 ;
;
N – мощность ракетной струи;
c – дополнительно установленная скорость отбр. шасси;
 ;
;
 ;
;
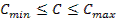
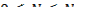
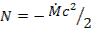 .
.
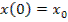 ;
;
 ;
;
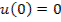 ;
;
 .
.

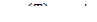

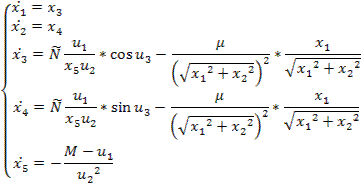

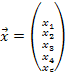
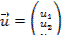
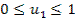
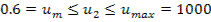
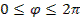
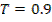
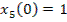


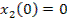


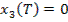

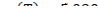
Оптимальное планирование поставок продукции.
Пример:
(1) 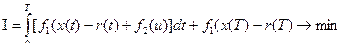
(2) 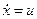
(3) 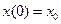
Решим задачу с помощью принципа max. Составим функцию Понтрягина:
(4) 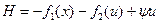
Записываем систему дифференциальных уравнений:

(5)
(6)
(7) 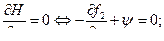
(8) 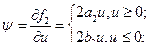
Из этого уравнения выразим уравнением через 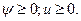
(9) 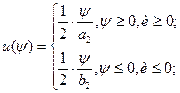
Подставим u(ψ) в (5):
(10) 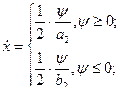
Краевое условие найдем продифференцировав 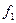 по
по 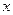 (T):
(T):
(11) 

 (12)
(12) 
Метод стрельбы для решения краевой задачи.
а) способ интегрирования.

(13)
(14)
 (15)
(15) 
(16)
Алгоритм. Задаем ψ0. Произвольно x0. Вычисляем по формулам (15), (16) x1,ψ1  x2,ψ2
x2,ψ2  …
…  x(T), ψ(T).
x(T), ψ(T).
В силу (122):
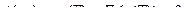 или
или 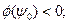
Задача о об оптимальноё поставке продукции
Пример:
(1) 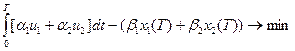
(2)  ;
; 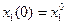 ;
;
(3) 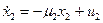 ;
; 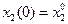 ;
;
(4) 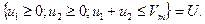
Формула функции Понтрягина:
(5) 
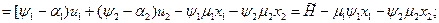

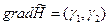
Согласно принципу max 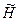 (
( 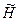 → max) :
→ max) :
u1=0 u2=0 
u1=Vm u2=0 
u1=0 u2=Vm 
Составляем сопряженную систему:
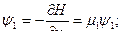
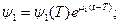
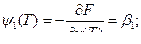
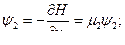
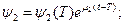
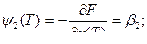
Получим зависимость 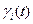 :
:
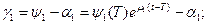
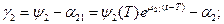

Итак получим  и можем вычислить значения функционала
и можем вычислить значения функционала 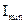 .
.
Задача об оптимальном управлении отраслью
Пример :
(1) 
(2) 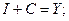
(3) 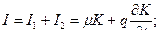
(4) 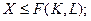
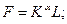
(5) 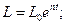
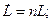
(6) 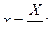

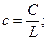
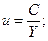

 ;
;
(7) 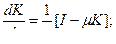
(8) из (2) 
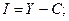

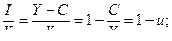
(9) из (1) 


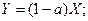
(10) из (8) и (9) 
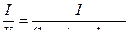

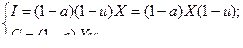
(11) из (7) и (10) 

(12) из (11) и (4) 
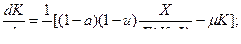
(13) из (11) и (6) 
 =
=
= 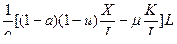 =
= 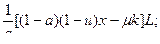
(14) из (13) и (5) 
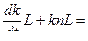
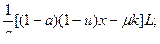

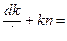
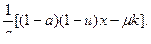
(15) Пусть q=1, тогда из (14) 
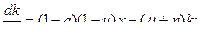
(16) из (4) и (6) 


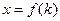 , т.к.
, т.к. 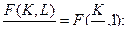
Предположим, что 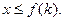
(17) 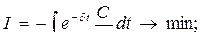
(18) 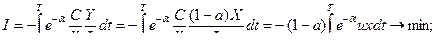
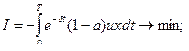

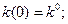

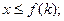
Механическая модель экономической задачи.
(1) 

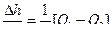

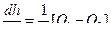 ;
;
(2) 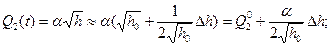
(3) из (1) и (2) 

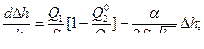
Обозначим 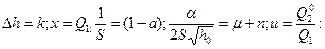
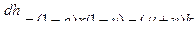 совпадает с (15).
совпадает с (15).
Задача об оптимальном выпуске продукции
Пример:
(1) 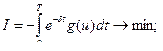
(2) 
(3) 
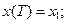
(4) 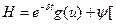
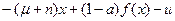 ];
];
(**)(5) 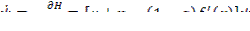
(6) 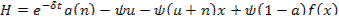
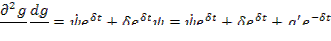
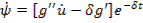
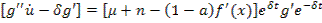
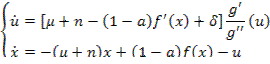
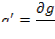
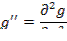
Пример 12.
Динамическая модель макроэкономической системы.
Введем следующие обозначения:
а – коэффициент производственного потребления  ;
;
μ – коэффициент амортизации;
n – темп роста трудовых ресурсов;
q – параметр модели;
ws – природные ресурсы;
u – доля потребления;
k – производственные финансы (основные);
X – валовый продукт;
Y – конечный продукт;
W – производственное потребление;
С – непроизводственное потребление;
I – капиталовложение;
I1 – амортизация отч?;
I2 – чистое капиталовложение;
F – производственная функция.
(1)  (1а)
(1а)
(2)  (2а)
(2а)
(3) 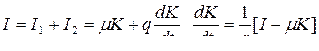
(4) 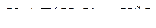
(5)  (5а)
(5а)
(6) 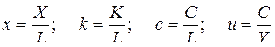
(7) 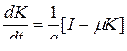

(8) из (2а): 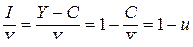
(9) из (1),(1а): 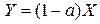

(10) из (8),(9): 
(11) из (7),(10): 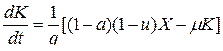

(12) из (4),(11): 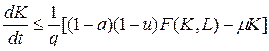
(13) из (6),(11): 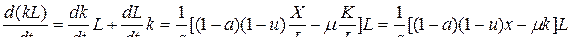
(14) из (5),(13): 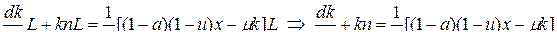

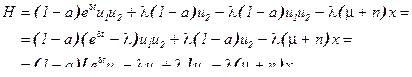

[1] Условие  (или
(или 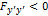 ) часто называют усиленным условием Лежандра, а условием Лежандра называют неравенство
) часто называют усиленным условием Лежандра, а условием Лежандра называют неравенство 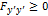 (или
(или 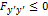 ).
).
Дата: 2018-11-18, просмотров: 370.