Теорема
А) Если функция 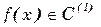 достигает экстремума в точке,
достигает экстремума в точке, 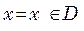 , то
, то  , для
, для 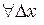
Замечание. Из равенства нулю диффуренцмала в точке, следует равенство в этой точке и производной.
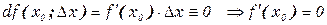
Б). Если функционал  имеющий вариацию достигает экстремума в точке,
имеющий вариацию достигает экстремума в точке, 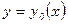 , то
, то 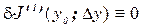 , для
, для  т.е. на кривых на которых достигается экстремум функционала, его вариация равна нулю.
т.е. на кривых на которых достигается экстремум функционала, его вариация равна нулю.
Доказательство.
При фиксированных  и
и  - функционал
- функционал  является функцией, от a, которая по предположению при a. = 0 достигает экстремума. Следовательно производная равна нулю
является функцией, от a, которая по предположению при a. = 0 достигает экстремума. Следовательно производная равна нулю
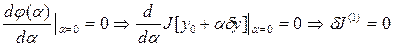
ч.т.д.
Ряд Тейлора.
А).
1.Для функции одной переменной 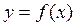 ряд Тейлора в точке
ряд Тейлора в точке  (которую не будем указывать) записывается в виде
(которую не будем указывать) записывается в виде
 или
или
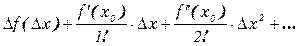
2. Для функции нескольких переменных можно записать аналогичное разложение. Например двух переменных:
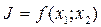 ;
;

или
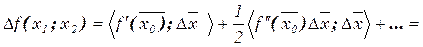
или
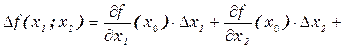
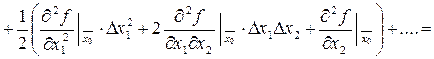
Б) Для функционала  имеющего вариации
имеющего вариации
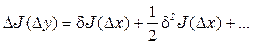
Замечание. Здесь знак вариации 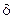 имеет по сути тот же смысл, что и знак дифференциала d для функции.
имеет по сути тот же смысл, что и знак дифференциала d для функции.
Рассмотрим функционал, наиболее часто рассматриваемый в теории вариационного исчисления 
Далее мы получим, что первая вариация равна
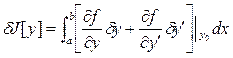
вторая вариация равна
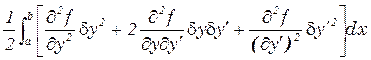
если подынтегральная функция достаточное число раз дифференцируема по переменным.
Первая вариация функционала вида и необходимое условие экстремума
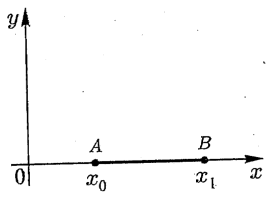
Пусть дан функционал
 ,
,
причем граничные условия заданы в виде фиксированных условий:
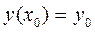 ;
; 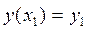 .
.
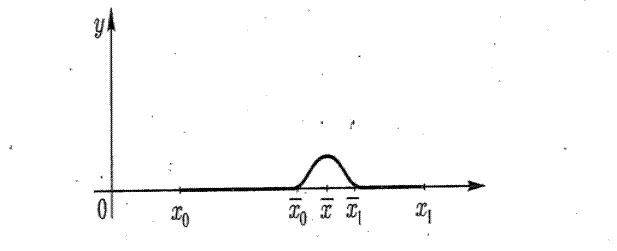
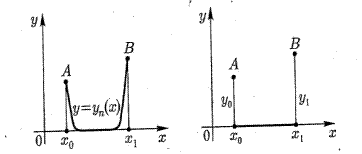
Предположим , что экстремум достигается на дважды дифференцируемых функциях. Берём какаю нибудь допустимую кривую. 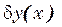 близкую к
близкую к  и получим функцию зависящую от параметра a.
и получим функцию зависящую от параметра a.
 .
.
Отметим, что 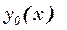 и
и  функции фиксированные, а параметр a переменная величина.
функции фиксированные, а параметр a переменная величина.
Запишем первую вариацию в смысле близости нулевого порядка
 .
.
Функционал тогда будет функцией j только от a
 .
.
Производная j(x) будет равна нулю в точке экстремума:
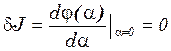
Получим

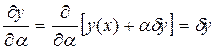

Тогда

необходимое условие экстремума
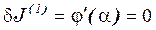 (10).
(10).
Уравнение Эйлера
Исследуем на экстремум функционал
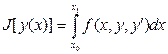 (1)
(1)
где  трижды непрерывная функция по всем аргументам.
трижды непрерывная функция по всем аргументам.
Краевые условия
 ,
, 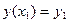 (2)
(2)
Необходимое условие экстремума
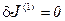 (3)
(3)
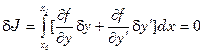
 ,
, 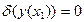 (4)
(4)
Интегрируя по частям, 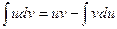 учитывая
учитывая
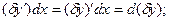
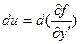 =
= 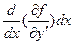 ;
;
получим
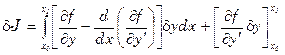 =0; (6)
=0; (6)
Или учитывая (4)
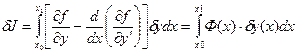
Основная лемма вариационного исчисления
Теорема: Если для каждой непрерывной функции 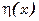 следующий функционал равен нулю
следующий функционал равен нулю

Где функция 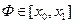 непрерывна на отрезке, то
непрерывна на отрезке, то
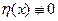
 (1)
(1)
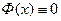 на том же отрезке.
на том же отрезке.
Доказательство. (2)
Пусть 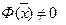 в некоторой точке
в некоторой точке  . В силу её непрерывности она сохраняет знак и в некоторой окпестности точки. , но тогда выбпрая произвольно и функцию
. В силу её непрерывности она сохраняет знак и в некоторой окпестности точки. , но тогда выбпрая произвольно и функцию 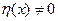 сохраняюшую знак на
сохраняюшую знак на 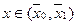 этой окрестности и равной нулю
этой окрестности и равной нулю 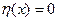 при
при 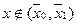 в других точках отрезка, получим
в других точках отрезка, получим
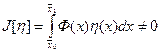 , что противоречит условию теоремы. Следовательно, предположение том, что функция не равна нулю хотя бы в одной точке отрезка, неверно и
, что противоречит условию теоремы. Следовательно, предположение том, что функция не равна нулю хотя бы в одной точке отрезка, неверно и 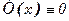 в любой точке отрезка.
в любой точке отрезка.
Применяя основную теорему вариационного исчисления к равенству

получим (7а)
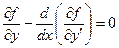
Или беря полную производную получим
 (7б)
(7б)
Это уравнение и называется уравнением Эйлера.
Примеры:
1) 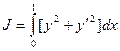 ,
, 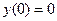 ,
, 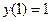
Применяя уравнение Эйлера получим дифференциальное уравнение второго порядка
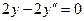
Записываем характеристическое уравнение
 и находя корни
и находя корни 
Получим общее решение дифференциального уравнения
 ,
,
Используя граничные условия получим частное решение
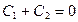 ,
, 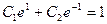 ,
, 

Это и есть экстремаль. Экстремум функционала может достигаться толко на этой кривой.
2) 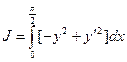 ,
, 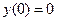 ,
, 
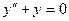 ,
, 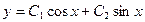 ,
, 
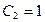
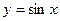
3)  ,
, 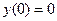 ,
, 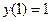
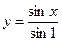
4) 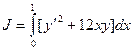 ,
, 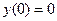 ,
, 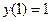
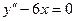 ,
,  ,
, 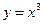
Частные случаи функционала
Пусть дан функционал

Заданы краевые условия
 ,
, 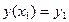
Рассмотрим частные случаи вида функции  интегрируемости уравнения Эйлера.
интегрируемости уравнения Эйлера.
1) 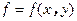 - подынтегральная функция не зависит от производной
- подынтегральная функция не зависит от производной 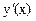
Уравнение Эйлера имеет вид
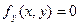
Это есть алгебраическое уравнение, не содержащее произвола и поэтому не удовлетворяющее в общем случае граничным условиям. Решения, вообще говоря, не существует.
Пример:
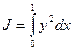 ;
;  ,
, 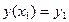
Уравнение Эйлера
 ;
; 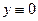 ;
;
2) Функция f линейно зависит от производной
Тогда уравнение Эйлера имеет вид
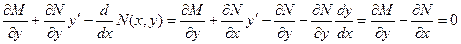
Но это опять алгебраическое уравнение.
Здесь можно различить два случая
а) 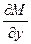 =
=  -алгебраическое уравнение
-алгебраическое уравнение
б)  -тождество, тогда функционал есть полный дифференциал и его значение не зависит от на допустимых кривых. Вариационная задача теряет смысл.
-тождество, тогда функционал есть полный дифференциал и его значение не зависит от на допустимых кривых. Вариационная задача теряет смысл.
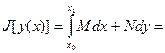

Примеры:
а) 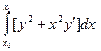 ,
, 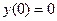 ,
, 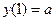
Решение
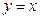
Первое граничное условие удовлетворяется, а второе только при a = 1
б)  ,
,
Уравнение Эйлера превращается в тождество. Значение функционала не зависит от пути интегрирования.
3)
Функция зависит только от производной
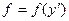
Общее уравнение Эйлера имеет вид 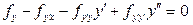
принимает вид
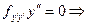
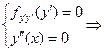

Все решения прямые.
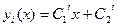
Пример:
а) Найти кривую, соединяющую две точки и имеющую наименьшую длину.
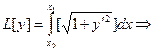

б) Задача брахистохроны, имеющей скорость зависящую от производной
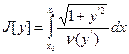 с.36.
с.36.
4) Подынтегральная функция не зависит от y.



Уравнение Эйлера
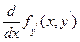

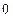
Имеет первый интеграл
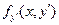

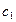
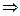



Пример. Пусть знаменатель в задаче о брахистохроне равен x. Это означает что скорость скатывания пропорциональна координате x.
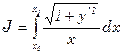
Первый интеграл
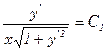
Первый способ решения
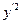

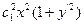


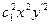
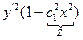 =
= 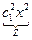
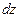

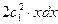
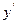


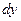

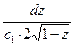
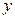




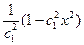

 ;
; 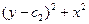
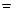
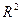

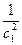
Второй способ решения.
Введём параметр
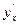

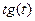
Тогда
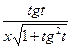


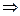
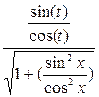

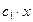
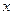

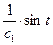

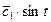
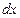


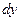

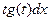

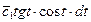


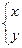

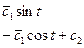
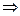
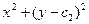



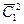
5) Пусть подынтегральная функция зависит от y и y’ и не зависит от x.
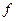

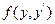



Если почтенно умножить уравнение на 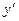 , прибавить и вычесть слагаемое
, прибавить и вычесть слагаемое  то нетрудно проверить, что получается полная производная
то нетрудно проверить, что получается полная производная
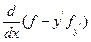

 .
.
Имеется первый интеграл.
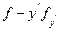 =
= 
5) Пример о наименьшей поверхности вращения.
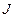 =
= 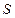 =
= 
Решение.
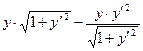 =
= 
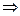
 =
= 
Делаем подстановку
 =
=  ,
,  =
=  ,
, 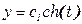 , где
, где  ,
,
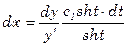 =
= 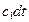 ,
,
 ,
,
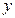 =
= 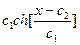 - цепная линия
- цепная линия
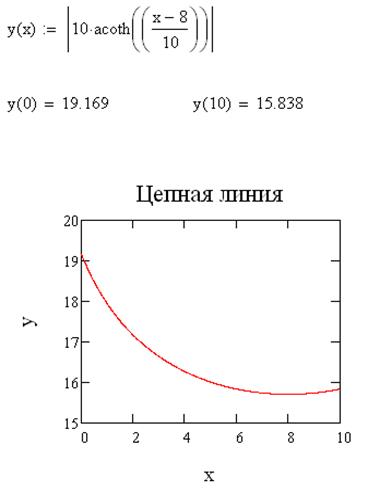
6) Задача о брахистохроне
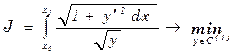

 =
= 
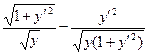 =
= 
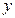 =
= 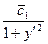 ;
; 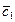 =
= 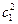
 =
=  ;
;
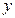 =
=  =
= 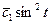 ;
;
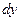 =
= 
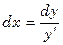
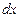 =
= 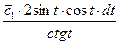 =
= 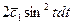
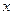 =
=  =
= 
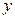 =
= 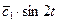 =
= 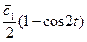
Задача Пуанкаре
История пятого постулата геометрии Евклида. Изложение упрощено.
Подробно см. Н.В. Ефимов “Высшая геометрия”. Наука . 2002. 575 с.
Евклид, жил приблизительно от 330 до 275 года до нашей эры. Составленные им начала содержат 8 определений, 5 постулатов и 9 аксиом.
Определения.
1.Точка есть то, что не имеет частей.
2.Линия есть длина без ширины.
3.Границы линии суть точки.
4.Прямая есть линия одинаково расположенная ко всем своим точкам.
5.Плоскость есть то, что имеет только длину и ширину.
6.Границы поверхности есть линии.
7.Плоскость есть поверхность одинаково расположенная ко всем своим прямым.
8.Плоский угол есть взаимное наклонение двух встречающихся линий, расположенных в одной плоскости.
Далее следует список основные утверждения (постулаты и аксиомы)
С современной точки зрения нет разницы между постулатами и аксиомами и неясно, какой принцип имел в виду Евклид разбивая основные утверждения на два класса.
Постулаты
1.Через две точки проходит прямая и притом одна.
2.Каждую прямую можно неограниченно продолжить в обе стороны.
3.Из любой точки можно описать окружность любого радиуса.
4.Все прямые углы равны.
5. Если дана прямая и точка вне её, то через точку проходит прямая параллельная данной прямой и притом только одна.
Аксиомы
6.Равные порознь третьему тоже равны.
7.Если к равным прибавить равные, то и получим равные.
8.Если от равных отнимем равные, то и получим равные.
9.Если к неравным прибавим равные, то получим неравные.
10.Если удвоить равные, то получим равные
11.Половины равных равны.
12.Совмещающиеся движением равны.
13.Целое больше любой части.
14.Две прямые не могут заключать пространства.
С точки зрения современной геометрии изложение геометрии на основе 14 основных утверждений следует признать неудовлетворительным во многих отношениях. Прежде всего определения оперируют такими понятиями, которые сами должны быть определены: граница, длина, и т.д. и ни одно не используется при доказательстве каких либо теорем. Что же касается 14 первичных утверждений, то они в целом существенны, но слишком бедны для безукоризненного логического развертывания геометрии, потому что многие факты опираются на наглядность чертежа. Утверждение 5 выглядит как теорема, которую следовало бы доказать на основе 13 других утверждений. Возможно сам Евклид пытался доказать пятый постулат. До конца 19 столетия было предложено много доказательств 5 постулата, но все они оказались ошибочными. Если бы собрать все труды, посвящённые 5 постулату, то они составили бы большую библиотеку.
Из многочисленных работ посвящённых проблеме 5 постулата следует выделить работы Саккери 1733 и Ламберта 1766. В результате их работ появилось гипотеза о том, что 5 постулат не может быть доказано на основе других 13. Ламберт далее, кто либо до него шел по правильному пути и видимо предчувствовал правильное решение проблемы. Ламберт писал: “Доказательство 5 постулата может быть доведено столь далеко, что остаётся по видимому ничтожная мелочь. Но при тщательном рассмотрении оказывается, что в этой мелочи как раз и содержится вся суть вопроса: обыкновенно она содержит равносильное 5 постулату утверждение и получается порочный логический круг. Я думаю, что все попытки доказательства 5 постулата невозможны.” Значительный вклад в раскрытие истинного смысла 5 постулата внесли также Лежандр, Швейкарт, Тауринус. Однако истинный смысл этого постулата был понят только Гауссом, Больяи и Лобачевским. Причем Лобачевскому принадлежит приоритет наиболее полного освещения проблемы в открытой печати. Если неевклидову геометрии сравнить с огромным деревом, то исследования Гаусса относятся к корням этого дерева, исследования Больяи - к ветвям, а Лобачевского ко всему дереву в целом. История этих исследований черезвычайна поучительна, однако суть может быть выражена в немногих словах.
Анализируя многовековые попытки доказательства 5 постулата, Лобачевский делает гипотезу, о его недоказуемости на основе остальных 13 утверждений. Далее Лобачевский делает вывод, раз нельзя доказать 5 постулат, то заменив его другим утверждением, противоположным утверждением, можно построить другую геометрию.
Аксиома Лобачевского формулируется так:
Через точку, вне данной прямой на плоскости, можно провести более одной прямой, не пересекающую данную прямую.
Появляются понятия непересекающихся и параллельных прямых. В Евклидовой геометрии есть только параллельные прямые.



Введение этих отличий не так просто и поэтому долгое время геометрию Лобачевского мало кто принимал. Из рисунка видно, что через точку вне прямой проходит три класса прямых: 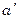 правая и
правая и  левая - параллельные прямые,
левая - параллельные прямые, 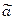 - непересекающиеся прямые,
- непересекающиеся прямые, 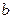 - пересекающиеся прямые. Однако модельные построения сыграли огромную роль в наглядном отображении сути всех абстрактных логических построений Лобачевского.
- пересекающиеся прямые. Однако модельные построения сыграли огромную роль в наглядном отображении сути всех абстрактных логических построений Лобачевского.
§11.Модель Пуанкаре и неевклидова геометрия Лобачевского.
Согласно принципу Ферма путь светового луча, распространяющегося в неоднородной среде является экстремалью вариационной задачи
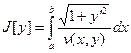
Если скорость зависит только от y, то получим вариационную задачу
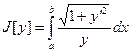
Поскольку подынтегральная функция не содержит явно x , то запишем первый интеграл
 =
= 
После упрощений получим
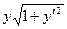 =
=  =
= 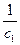
Решаем дифференциальное уравнение
 =
= 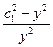
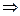
 =
= 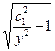
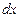 =
=  ;
; 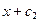 =
= 
Получаем общее решение зависящее от двух констант.
 =
=  =
= 
Это окружности центр которых находится на оси x. Через две любые точки верхней полуплоскости проходит единственная экстремаль q.
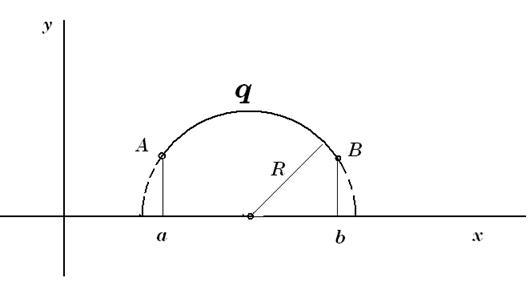
Оптической длиной кривой q( x) назовется значение интеграла 
Будем рассматривать верхнюю плоскость как оптическую среду в которой скорость света v в каждой точке равна ординате  . Лучами света в этой среде будут полуокружности. Если одна или обе точки А и В лежат на оси x , то значение оптической длины экстремали будет равна бесконечности.
. Лучами света в этой среде будут полуокружности. Если одна или обе точки А и В лежат на оси x , то значение оптической длины экстремали будет равна бесконечности.

Модель Пуанкаре относится к большим расстояниям, вопазмерным размерам вселенной. Условный рисунок части вселенной. Скопления галактик и прямая между удалёнными точками..
Поэтому точки лежащие на оси Ох будем называть бесконечно удалёнными. Будем называть линии по которым распространяется свет (окружности на плоскости) прямыми, оптические длины экстремалей между точками А и В просто длинами. Две прямые могут пересекаться.
Две прямые имеющих общую бесконечно удалённую точку - параллельными прямыми. Легко видеть, что все утверждения Евклида справедливы на плоскости с такими прямыми, за исключением 5 постулата, вместо него дсправедлив постулат Лобачевского. 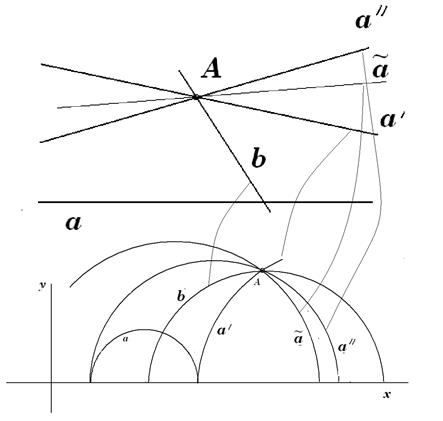
Через точку А вне прямой a проходят три класса прямых: 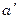 правая и
правая и 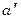 левая - параллельные прямые,
левая - параллельные прямые,  - непересекающиеся прямые,
- непересекающиеся прямые, 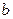 - пересекающиеся прямые. §12 Численные способы решения. Примеры задач.
- пересекающиеся прямые. §12 Численные способы решения. Примеры задач.
12. Численные методы
12.1. Метод стрельбы
Пусть дана вариационная задача
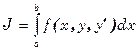 ;
; 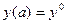 ;
; 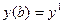
Уравнение Эйлера есть дифференциальное уравнение второго порядка.
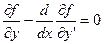
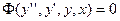
Разрешим его относительно второй производной, это часто можно сделать. Если нельзя, то алгоритм немного усложняется.
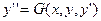
Граничные условия при
При
x=a :  ;
;
x=b: 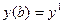
Общее решение зависит от 2 констант
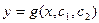
Корректность краевой задачи будет определяться возможность решения системы полученной из общего решения, при подстановке в нею граничных условий.

Заменим производные разделёнными разностями.
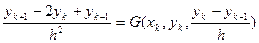
Тогда для интегрирования явным методом для получения значения функции в новой точке необходимо знание значений в двух предыдущих
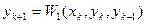
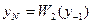 ;
; 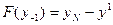
Пример:
Рассмотрим простой учебный пример

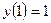
 (8)
(8)
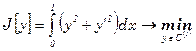 (9)
(9)
Полученное с помощью уравнения Эйлера решение рис.2 даётся равенством
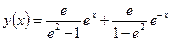
Сравнение с решением полученном числено показано на рис.

Второй пример
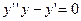

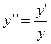
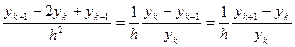
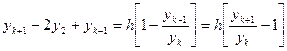
1. 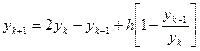
2. 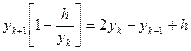 ;
; 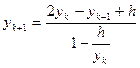
12.3.Метод Ньютона (конечных разностей).
Пусть дано уравнение Эйлера
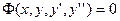

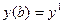
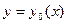
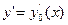
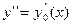
Разложим в ряд Тейлора
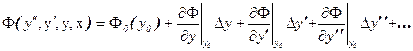
Требуется решить уравнение
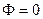
Ограничимся только 4 слагаемыми
Это линейное уравнение
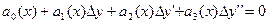
Задавая начальное нулевое приближение 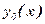
И решая дифференциальное уравнение с краевыми условиями
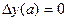 ,
, 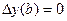 ,
,
 ,
, 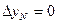 .
.
получим первое приближение
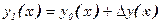
Пример:
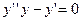
 ,
, 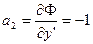 ,
, 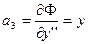 ;
;
 ,
,
Возьмём линейную функцию
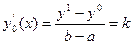 ,
,
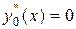 ,
,
Подставим в уравнение
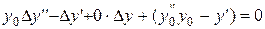
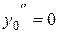 ,
, 
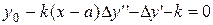
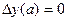 ;
; 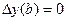

Получим разностную схему
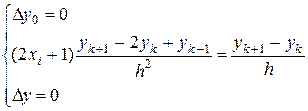 ,
, 
Это есть система линейных уравнений
Дата: 2018-11-18, просмотров: 339.