При больших скоростях сила пропорциональна скорости движения в квадрате.
;
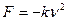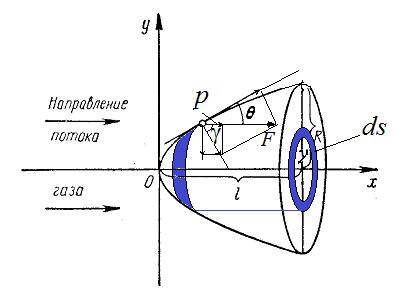
Давление оказываемое средой коллинеарно силе F.
Нормальное давление равно после двукратного проектирования равно.
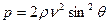
Тогда дифференциал силы равен
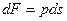
где ds – дифференциал площади в сечении
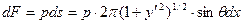или подставив p получим дифференциал силы
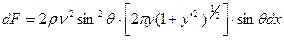
Функционал есть вся сила действующая на поверхность
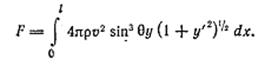
Будем считать, что угол мал
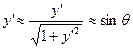
Тогда дифференциал и функционал упрощаются
;
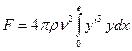Краевые условия при x = 0 и x = l
;
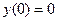
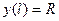Получаем уравнение Эйлера
;
;
;
;
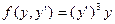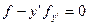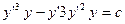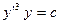Отсюда
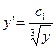и 
;
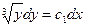Откуда получаем
;
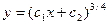Используя краевые условия получим
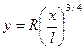или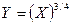 
;
Задачи содержащие несколько переменных
Пусть дана вариационная задача вида
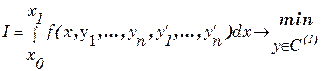
с краевыми условиями
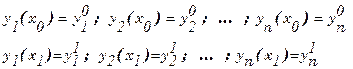
Доя получения необходимых условий будем варьировать лишь одну из функций
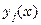, j =1,…, n
Оставляя остальные неизменными
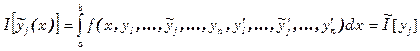
И следовательно функция реализующая экстремум должна удовлетворять уравнению Эйлера, а так как это рассуждение применимо для любого номера j то получим систему уравнений Эйлера, каждое из которых есть дифференциальное уравнение 2 го порядка
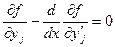, ( j=1,…, n) .
Пример 1:
Функционал зависит от двух кривых.
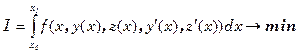
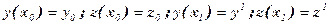
Варьируя сначала y( x) затем z( x) получим два уравнения Эйлера
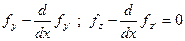
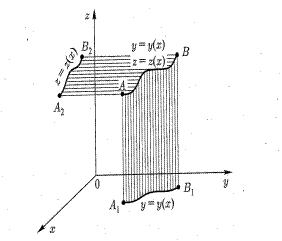
Пример2:
Найти экстремали функционала
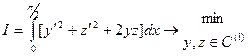
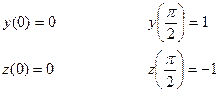
Система имеет вид
,
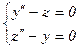Из первого находим
,
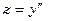Дифференцируя два раза получим
,
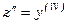Подставляя во второе уравнение имеем
.
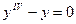Линейное дифференциальное уравнение 4 го порядка легко решается и получаем общее решение
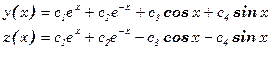
Используя граничные условия находим
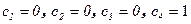, следовательно
, 
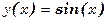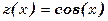
Пример 3:
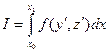
Система уравнений Эйлера имеет вид
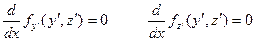
откуда
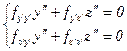
Считая, что
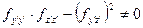
Получим общие решения
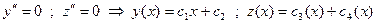
Задача с производными более высокого порядка
Исследуем функционал вида
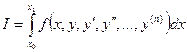
С граничными условиями
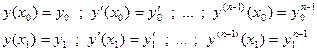
В граничных точках задана функция и её n-1 производных.
Рассмотрим однопараметрическое семейство функций
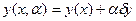
Вычислим вариацию раскладывая в ряд Тейлора или дифференцируя по параметру
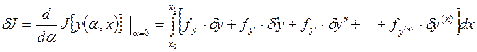
Интегрируем по частям нужное количество раз
один раз
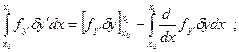
два раза
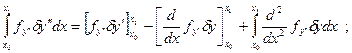
три раза
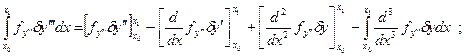
и так далее
n раз
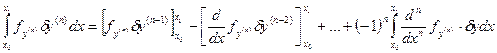
Получим вариацию
;
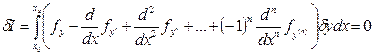По основной лемме вариационного исчисления получим дифференциальное уравнение n - го порядка
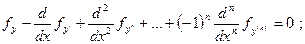
Которое называется уравнением Эйлера -Пуассона
Пример 1:
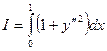
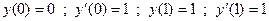
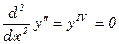
Общее решение есть полином третье степени
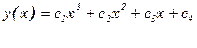
Дифференцируя
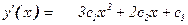
И используя краевые условия получи решение
,
,
,
.
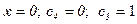
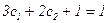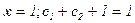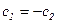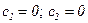
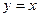Пример 2:
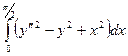
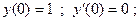
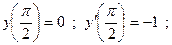
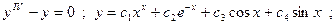
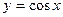
Пример 3:
Задача об изгибе упругой однородной балки, заделанной на концах в неподвижную среду, имеющей длину 2L. Балка под действием своего веса изгибается и можно показать, что её изгиб определяется экстремалями функционала (достигается минимум потенциальной энергии):
.
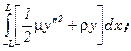
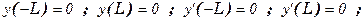
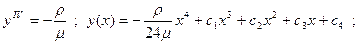
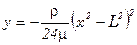Дата: 2018-11-18, просмотров: 402.
