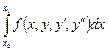
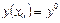
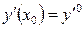
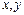 - свободные
- свободные

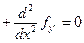
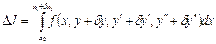
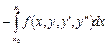
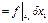
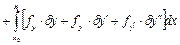
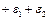
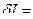
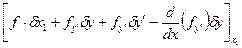
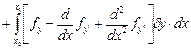 ;
;

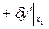
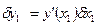
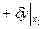
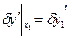

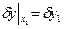
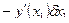
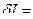

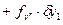
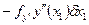
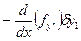
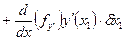
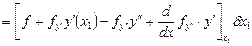
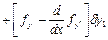
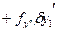
Все свободные, то имеем 
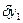
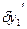
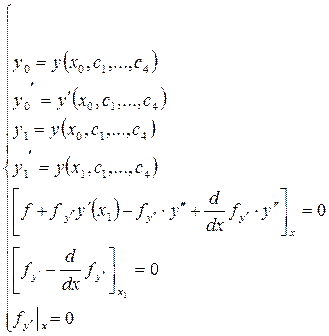
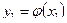
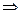
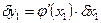
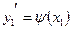
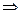
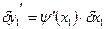 …
…
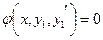

Пример:
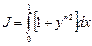
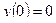
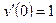
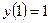
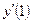 - произвольная
- произвольная
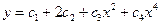
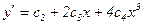
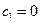

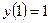
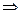
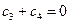
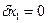
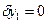 то
то
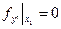

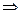
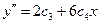
Достаточные условия экстремума
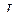 :
: 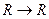
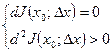
 - достататочные условия точки минимума
- достататочные условия точки минимума
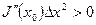
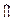
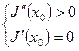
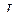 :
: 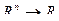
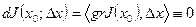

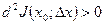
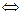

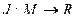
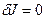
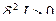
Некоторые определения

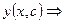
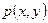
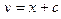
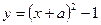
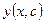
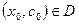
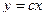
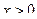
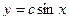 а)
а) 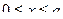 ;
; 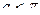
б) 
в) 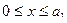 ;
;  поле не образуется
поле не образуется
Поле экстремалей
3) 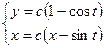
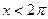
4) 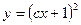
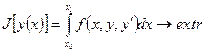
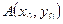 ;
; 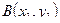
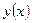 - экстремаль
- экстремаль 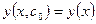
Пример:
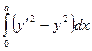
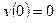 ;
; 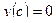
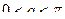
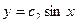
Известно… 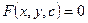 - семейство
- семейство 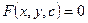
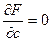
Пример: 1)  - огибающая
- огибающая
2)  - узел
- узел 
3)  - т. заострений
- т. заострений
4) 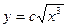 - т. заострений
- т. заострений
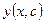
 близкие кривые семейства будут пересекаться вблизи Ф
близкие кривые семейства будут пересекаться вблизи Ф
Пример: 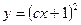
Аналитическое условие Якоби
Пусть 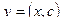 ; А;
; А; 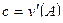 ;
; 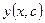 - решения уравнения Эйлера
- решения уравнения Эйлера 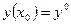
 ;
; 
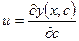 ;
;  - обозначим
- обозначим

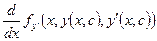
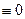
Дифференцируем по с
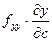
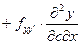
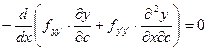
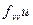
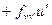
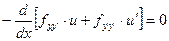

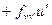
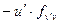
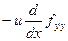

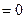
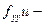
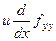
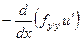
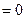

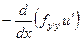
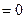 - уравнение Якоби
- уравнение Якоби
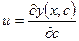
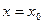

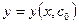 ;
;  (или
(или 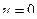 )
)
Пример: 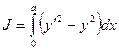
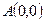
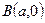
Уравнение Якоби 
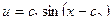
Т.к. 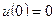
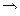
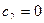
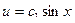
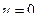
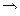
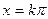
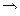 если
если 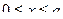 и функция
и функция  обращается в нуль
обращается в нуль 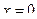 и условие Якоби выполнено;
и условие Якоби выполнено;
если 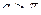 , то
, то 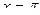 -
-  обращается в нуль в т.
обращается в нуль в т. 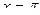 и условие Якоби не выполнено
и условие Якоби не выполнено
Пример: 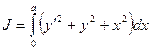

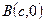
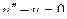
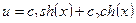
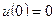
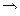
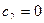
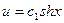
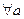 условие Якоби выполнено
условие Якоби выполнено
Функция 


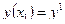
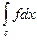

Приращение 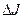 при переходе от С на некоторую близкую допустимую кривую
при переходе от С на некоторую близкую допустимую кривую 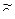 есть
есть
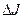

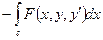
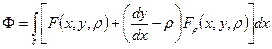
 т.к.
т.к. 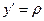

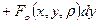 явл-ся интегралом от точного дифференциала
явл-ся интегралом от точного дифференциала
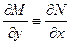
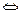

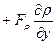

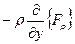
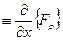
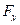
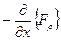
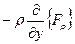
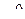
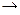
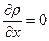
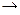
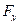
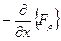
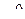 ;
; 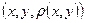
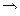
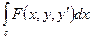
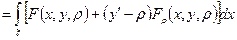 не зависит от выбора траектории
не зависит от выбора траектории 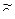
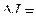
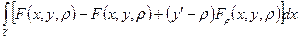
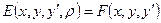
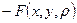
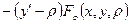
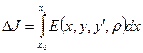
Достаточное условие
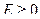 , то и
, то и 
 , то
, то 
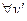 ~
~ 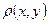
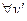
Достаточные условия экстремума
кривые должны быть экстремалями
экстремаль может быть включена в поле экстремалей
Пример 1:
I= 
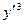 dx y(0)=0 y(a)=b a>0; b>0
dx y(0)=0 y(a)=b a>0; b>0
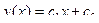
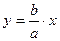
 =
= 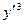 -
- 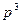 -3
-3 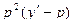 =(
=( 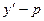 )(
)( 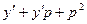 )-3
)-3 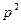 (
( 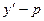 )= =(
)= =(  )[
)[ 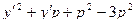 ]=(
]=( 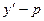 )[
)[  (
( 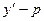 )]=(
)]=( 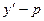 )
) 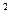 [
[ 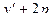 ]
]
Если 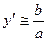 то
то 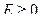 ; если
; если 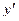 - var, то второй сомножитель может принять и <0.
- var, то второй сомножитель может принять и <0.
Пример 2:
Пример 2. Исследовать на экстремум функционал
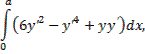
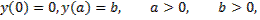
в классе непрерывных функций с непрерывной первой производной.
Экстремалями являются прямые 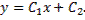 Граничным условиям удовлетворяет прямая
Граничным условиям удовлетворяет прямая 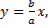 которая включается в пучок экстремалей
которая включается в пучок экстремалей 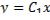 , образующих центральное поле. Функция
, образующих центральное поле. Функция
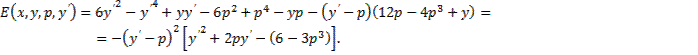
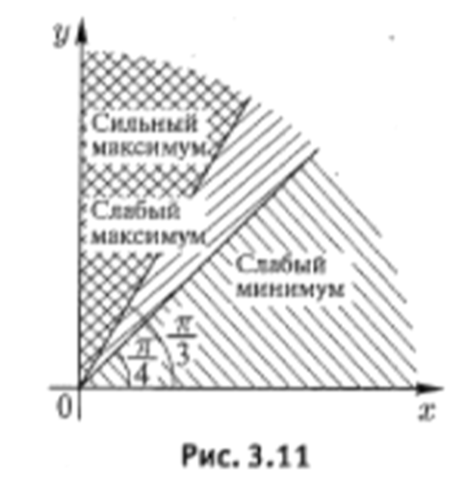
Знак функции 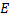 противоположен знаку последнего множителя
противоположен знаку последнего множителя  . Этот множитель обращается в нуль и может изменить знак лишь при переходе
. Этот множитель обращается в нуль и может изменить знак лишь при переходе  через значение
через значение 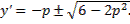 При
При 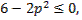 или
или  , при любом
, при любом 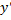 имеем
имеем
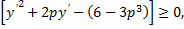
если же 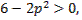 или
или 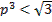 , то выражение
, то выражение

меняет знак. Если же при этом 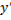 достаточно мало отличается от
достаточно мало отличается от 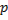 , то последнее выражение сохраняет положительный знак при
, то последнее выражение сохраняет положительный знак при 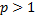 и отрицательный знак при
и отрицательный знак при 
Следовательно, при 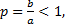 или
или  имеем слабый минимум, так как
имеем слабый минимум, так как 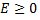 при значениях
при значениях 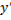 , близких к
, близких к 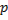 ; при
; при 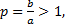 или
или 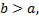 имеем слабый максимум. При
имеем слабый максимум. При 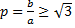 имеем сильный максимум, так как
имеем сильный максимум, так как 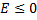 при любых значениях
при любых значениях 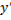 . При
. При 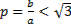 , на основании замечания на с. 119, нет ни сильного минимума, ни сильного максимума (рис. 3.11).
, на основании замечания на с. 119, нет ни сильного минимума, ни сильного максимума (рис. 3.11).
Даже в приведенных выше весьма простых примерах исследование знака функции 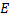 было сопряжено с некоторыми затруднениями, и поэтому желательно условие сохранения знака функции
было сопряжено с некоторыми затруднениями, и поэтому желательно условие сохранения знака функции 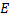 заменить более легко проверяемым условием. Предположим, что функция
заменить более легко проверяемым условием. Предположим, что функция  трижды дифференцируема по аргументу
трижды дифференцируема по аргументу 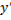 . По формуле Тейлора получим
. По формуле Тейлора получим

где 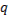 заключено между
заключено между 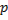 и
и 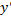 .
.
Функция 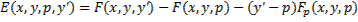 после замены функции
после замены функции 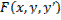 ее разложением по формуле Тейлора примет вид
ее разложением по формуле Тейлора примет вид
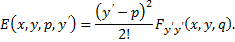
Отсюда видно, что функция 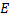 сохраняет знак, если сохраняет знак
сохраняет знак, если сохраняет знак 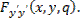 При исследовании на слабый экстремум функция
При исследовании на слабый экстремум функция 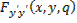 должна сохранять знак для значений
должна сохранять знак для значений 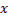 и
и 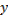 в точках, близких к точкам исследуемой экстремали, и для значений
в точках, близких к точкам исследуемой экстремали, и для значений 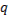 , близких к
, близких к 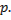 Если
Если 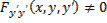 в точках экстремали
в точках экстремали 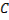 , то в силу непрерывности эта вторая производная сохраняет знак и в точках, близких к кривой
, то в силу непрерывности эта вторая производная сохраняет знак и в точках, близких к кривой 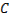 , и для значений
, и для значений 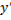 , близких к значениям
, близких к значениям 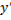 на кривой
на кривой 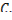 Таким образом, при исследовании на слабый минимум условие
Таким образом, при исследовании на слабый минимум условие 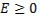 может быть заменено условием
может быть заменено условием 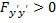 на экстремали
на экстремали 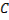 , а при исследовании на слабый максимум условие
, а при исследовании на слабый максимум условие 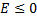 может быть заменено условием
может быть заменено условием 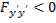 на кривой
на кривой 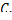 Условие
Условие 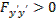 (или
(или 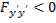 ) носит название условия Лежандра[1].
) носит название условия Лежандра[1].
При исследовании на сильный минимум условие 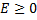 может быть заменено требованием
может быть заменено требованием 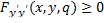 в точках
в точках 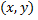 , близких к точкам кривой
, близких к точкам кривой 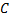 при произвольных значениях
при произвольных значениях 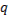 . При этом, конечно, предполагается, что разложение по формуле Тейлора
. При этом, конечно, предполагается, что разложение по формуле Тейлора
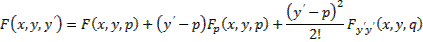
справедливо при любых 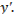 При исследовании на сильный максимум получим условие
При исследовании на сильный максимум получим условие 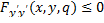 , при тех же предположениях относительно области изменения аргументов и разложимости функции
, при тех же предположениях относительно области изменения аргументов и разложимости функции  по формуле Тейлора.
по формуле Тейлора.
Пример 1:
Пример 3. Исследовать на экстремум функционал
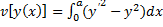 ,
, 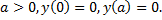
Уравнение Эйлера имеет вид 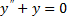 , его общее решение
, его общее решение 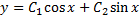 . Используя граничные условия, получаем
. Используя граничные условия, получаем  и
и  , если
, если 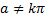 , где
, где 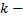 целое число.
целое число.
Итак, при 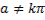 экстремум может достигаться лишь на прямой
экстремум может достигаться лишь на прямой 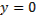 . Если
. Если 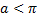 , то пучок экстремалей
, то пучок экстремалей 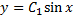 с центром в точке (0,0) образуют центральное поле. При
с центром в точке (0,0) образуют центральное поле. При 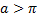 условие Якоби не выполнено (см с. 109).
условие Якоби не выполнено (см с. 109).
Так как подынтегральная функция трижды дифференцируема по 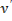 при любых
при любых 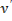 и
и 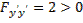 при любых значениях
при любых значениях 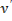 , то на прямой
, то на прямой 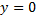 при
при 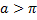 реализуется сильный минимум. Если учесть замечание на с. 114, то можно утверждать, что при
реализуется сильный минимум. Если учесть замечание на с. 114, то можно утверждать, что при 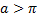 минимум на прямой
минимум на прямой 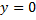 не достигается.
не достигается.
Пример 4. Исследовать на экстремум функционал
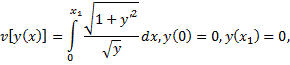
(см. задачу о брахистохроне, с. 40). Экстремалями являются циклоиды
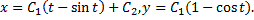
Пусть циклоид 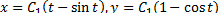 с центром в точке (0,0) образует центральное поле, включающее экстремаль
с центром в точке (0,0) образует центральное поле, включающее экстремаль
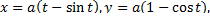
где 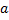 определено из условия продолжения циклоиды через вторую граничную точку
определено из условия продолжения циклоиды через вторую граничную точку 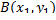 , если
, если 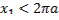 (рис. 3.12)
(рис. 3.12)
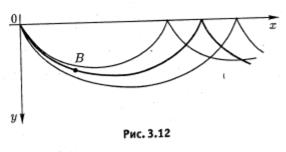
Имеем

при любых 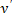 . Следовательно, при
. Следовательно, при 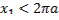 на циклоиде
на циклоиде
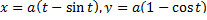
реализуется сильный минимум.
Пример 3:
Пример 5. Исследовать на экстремум функционал
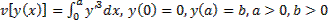 .
.
Этот пример был решен ранее, но теперь в отношении слабого экстремума исследование можно упростить.
Экстремалями являются прямые линии. Пучок 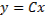 образует центральное поле, включающее экстремаль
образует центральное поле, включающее экстремаль 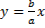 . На экстремали
. На экстремали  вторая производная
вторая производная 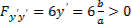 . Следовательно, прямая,
. Следовательно, прямая, 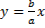 реализует слабый минимум. При произвольных
реализует слабый минимум. При произвольных 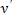 вторая производная
вторая производная 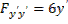 знака не сохраняет; следовательно, указанные выше достаточные условия для достижения сильного минимума не выполнены. Однако отсюда еще нельзя заключить, что сильный экстремум не достигается.
знака не сохраняет; следовательно, указанные выше достаточные условия для достижения сильного минимума не выполнены. Однако отсюда еще нельзя заключить, что сильный экстремум не достигается.
Пример 4:
Пример 6. Исследовать на экстремум функционал
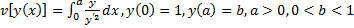 .
.
Первый интеграл уравнения Эйлера имеет вид
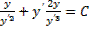 или
или  ,
,
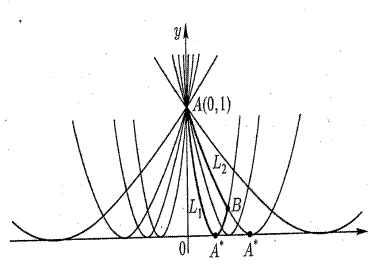
извлекая корень, разделяя переменные и интегрируя, получаем  - семейство парабол. Из условия
- семейство парабол. Из условия 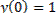 находим
находим 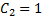 . Пучок парабол
. Пучок парабол 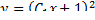 с центром в точке A(0,1) имеет
с центром в точке A(0,1) имеет 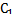 -дискриминантную кривую
-дискриминантную кривую 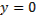 (рис.3.13). Через точку
(рис.3.13). Через точку  проходят две параболы этого пучка. На дуге АВ одной из них
проходят две параболы этого пучка. На дуге АВ одной из них  лежит точка
лежит точка 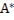 , сопряженная с точкой А, а на другой же
, сопряженная с точкой А, а на другой же 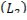 сопряженной точки нет, следовательно, на дуге
сопряженной точки нет, следовательно, на дуге 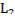 условие Якоби выполнено и на этой дуге параболы может реализоваться экстремум. В окрестности исследуемой экстремали
условие Якоби выполнено и на этой дуге параболы может реализоваться экстремум. В окрестности исследуемой экстремали 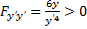 для произвольных
для произвольных 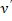 , однако на этом основании нельзя утверждать, что на дуге
, однако на этом основании нельзя утверждать, что на дуге 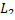 реализуется сильный минимум, так как функция
реализуется сильный минимум, так как функция 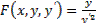 не может быть
не может быть
представлена в виде
при произвольных значениях  ввиду наличия разрыва функции
ввиду наличия разрыва функции  при
при 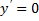 . Можно лишь утверждать, что на
. Можно лишь утверждать, что на 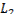 реализуется слабый минимум, так как для значений
реализуется слабый минимум, так как для значений 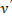 , близких к наклону поля на кривой
, близких к наклону поля на кривой 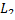 , такое разложение функции
, такое разложение функции 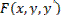 по формуле Тейлора имеет место. Для полного исследования этого функционала на экстремум необходимо рассмотреть функцию
по формуле Тейлора имеет место. Для полного исследования этого функционала на экстремум необходимо рассмотреть функцию  :
:
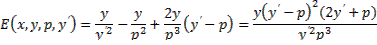
Так как множитель 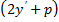 не сохраняет знака при произвольных
не сохраняет знака при произвольных 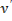 , то можно утверждать, что сильный минимум на дуге
, то можно утверждать, что сильный минимум на дуге 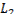 не достигается.
не достигается.
Изложенная теория без значительных изменений переносится и на функционалы вида
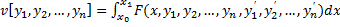 ,
,
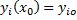 ,
, 
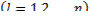
Функция 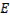 принимает вид
принимает вид
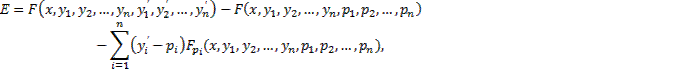
где 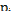 - функции наклона поля, на которое наложены некоторые ограничения (при этих ограничениях поле называется специальным).
- функции наклона поля, на которое наложены некоторые ограничения (при этих ограничениях поле называется специальным).
Условие Лежандра  заменяется следующими условиями:
заменяется следующими условиями:
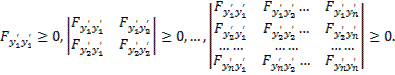
Достаточные условия слабого минимума как в простейшей задаче, так и в более сложных, можно получить иным методом, основанным на изучении знака второй вариации.
По формуле Тейлора преобразуем приращение функционала в простейшей задаче к следующему виду:
∆v=  ,
,
где R имеет порядок выше второго относительно 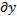 и
и 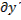 . При исседовании на слабый экстремум
. При исседовании на слабый экстремум 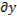 и
и 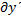 достаточно малы, и в этом случае знак приращения
достаточно малы, и в этом случае знак приращения 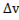 определяется знаком члена, стоящего в правой части и содержащего наиболее низкие степени
определяется знаком члена, стоящего в правой части и содержащего наиболее низкие степени 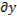 и
и 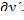 На экстремали первая вариация
На экстремали первая вариация
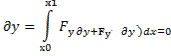
и,следовательно, знак приращения ∆v, вообще говоря, совпадает со знаком второй вариации.
Условие Лежандра в соединении с условием Якоби и являются условиями, а вместе с тем и постоянство знака приращения ∆v в задаче о слабом экстремуме.
Действительно, рассмотрим интеграл
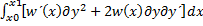 (3.2)
(3.2)
где w(x) – произвольная дифференцируемая функция. Этот интеграл равен нулю:
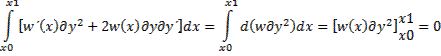
(так как ∂y  ).
).
Прибавляя интеграл (3.2) ко второй вариации, получим
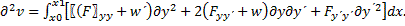
Выбираем функцию w(x) так, чтобы подынтегральная функция, с точностью до множителя, превратилась в точный квадрат, для чего функция w(x) должна удовлетворять уравнению
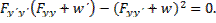
При таком выборе функции w вторая вариация принимает вид
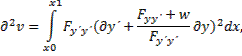
и следовательно, знак второй вариации совпадает со знаком 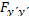 .
.
Однако такое преобразование возможно лишь в предложении, что дифференциальное уравнение
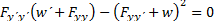
имеет на отрезке (  ) дифференцируемое решение w(x).
) дифференцируемое решение w(x).
Преобразовав это уравнение к номым переменным подставновкой w=-  , где u – новая неизвестная функция, получим
, где u – новая неизвестная функция, получим
( 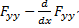 )u-
)u- 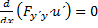 – уравнение Якоби(см. с. 114).
– уравнение Якоби(см. с. 114).
Если существует не обращающееся в нуль при 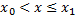 решение этого уравнения, т.е. выполнено условие Якоби, то существует для тех же значений x непрерывное и дифференцируемое решение w(x)=-
решение этого уравнения, т.е. выполнено условие Якоби, то существует для тех же значений x непрерывное и дифференцируемое решение w(x)=- 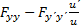 уравнения
уравнения
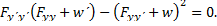
Итак, условие Лежандра и условие Якоби гарантируют сохранение знака второй вариации и, следовательно являются достаточным условием слабого минимума ( 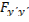 >0) или максимума(
>0) или максимума( 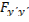 >0).
>0).
Экстремали с угловыми точками.
Задача отражения.
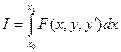
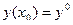

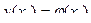
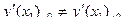


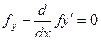



Подробнее:
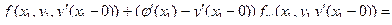
= 
Пример:
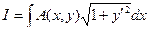
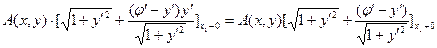
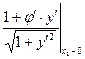 =
= 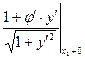
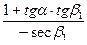 =
= 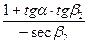
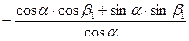 =
= 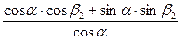
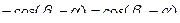
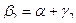
 =>
=> 
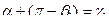 =>
=> 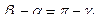
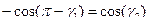
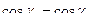 - угол падения равен углу отражения
- угол падения равен углу отражения
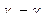
Преломление экстремалей.

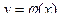
f= 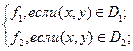
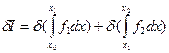
= 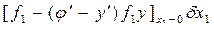 -
-  =0
=0
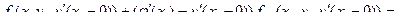
= 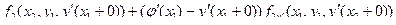
Пример:
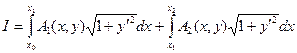
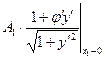 =
= 
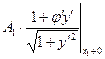
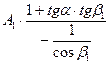 =
= 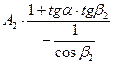
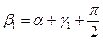

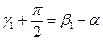
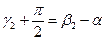
 =
= 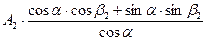
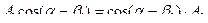
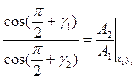
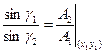
Условие существования угловой точки.
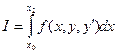
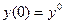
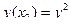
Пример 1:
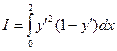 y(0)=0 y(2)=1
y(0)=0 y(2)=1
I  0
0

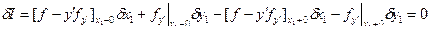

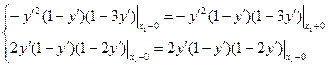
1) 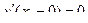
2) 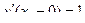
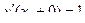
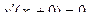
Пример 2:
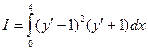
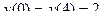
Пример 3:
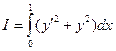


Односторонние вариации
 ,
, 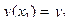
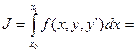
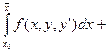
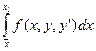
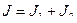
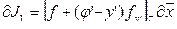
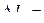
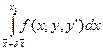 -
- 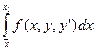 =
= 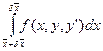 +
+ 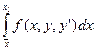 -
- 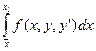 =
=
=  =
= 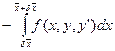
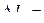
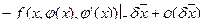

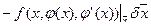
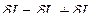 =[
=[ 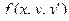 +
+ 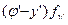
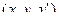 ]
] 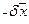
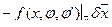 =
=
=[ 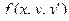
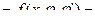
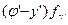
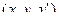 ]
]  =0
=0

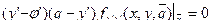
Либо 
Либо 

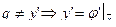
Задача Больца
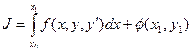
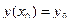 ,
, 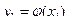
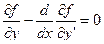
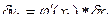

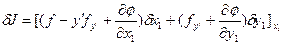
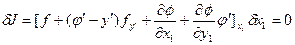
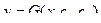
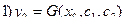
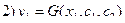
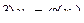
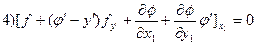
Пример 1:
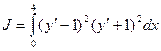 ,
,  ,
, 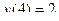
Пример 2:

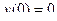 ,
, 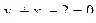
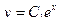

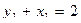
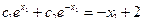
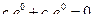
Дата: 2018-11-18, просмотров: 364.