Лекция 1
Задача о брахистохроне
В 1696 И.Бернулли опубликовал статью «О новой задаче к решению которой приглашаются математики». Это была задача о брахистохроне – задаче о линии быстрейшего спуска.

Задача.
Пусть заданы две точки А, В на плоскости и введена система координат (х,у). Требуется найти такую кривую (функцию) у(х), проходящую через А и В, так чтобы тяжелый шарик скатывался по этой кривой, без трения, достиг бы точки В за минимально возможное время.
Решение.
Решение задачи о брахистохроне было дано И. Бернулли, Я. Бернулли, Г. Лейбницем, И. Ньютоном и Г. Лопиталем. Линией быстрейшего ската не будет прямая, соединяющая точки А и В, хотя она и является кратчайшим расстоянием между точками А и В, так как при движении по прямой скорость движения будет нарастать сравнительно медленно, если же взять кривую, более круто спускающуюся около точки А вниз, то хотя путь и удлинится, но значительная часть пути будет пройдена с большей скоростью. Оказалось, что линией быстрейшего ската, является циклоида (брахистохрона).
Предположим, что начальная скорость скатывающейся точки равна нулю Воспользуемся законом сохранения. К моменту когда точка будет иметь координату y(x) рис.1 потенциальная энергия шарика уменьшится на величину mg·y, а кинетическая увеличится на величину mV2/2. В силу закона сохранения должно выполняться равенство:
 , (1)
, (1)
откуда
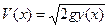 . (2)
. (2)
Дифференциал пути
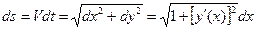 . (3)
. (3)
Дифференциал времени учитывая (2) и (3) равен
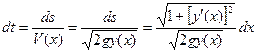 . (4)
. (4)
Беря определённый интеграл получим
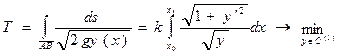 ,
, 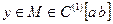 . (5)
. (5)
который дополняется краевыми условиями прохождения кривой через точки А и В
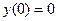 ,
, 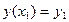 (6a,b)
(6a,b)
Решением вариационной задачи являются кривая, описываемая формулами
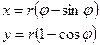 (7а, б)
(7а, б)
Формулы описывают траекторию точки на ободе колеса [ Справочник ]
Рассмотрим задачу со следующими условиями:
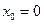
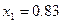 м.
м.

 м.
м.
Численно находится r и 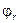
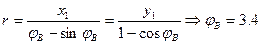 рад.
рад. 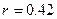 м.
м.
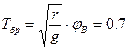 с.
с.
Время движения по наклонной плоскости равно.
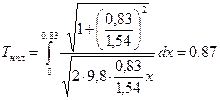 с
с
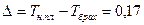 с
с
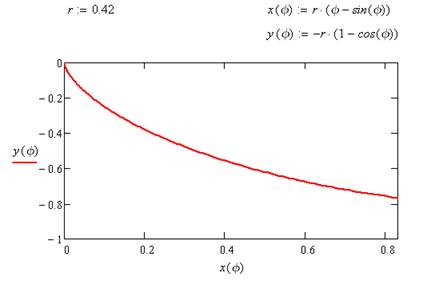
Рис.1. Линия быстрейшего спуска.
Пример 2:
Рассмотрим простой учебный пример
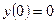
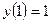
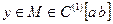 (8)
(8)
 (9)
(9)
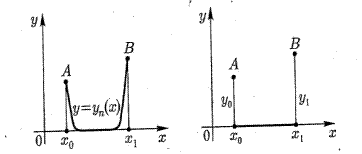
Полученное с помощью уравнения Эйлера решение рис.2 даётся равенством
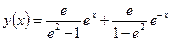 (10)
(10)
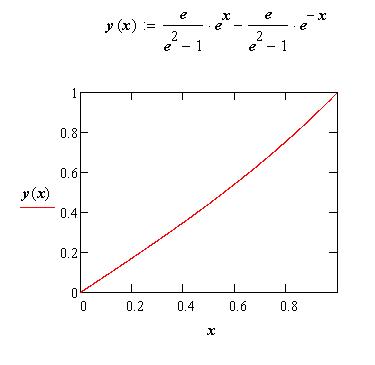
Рис.2. Экстремаль для функционала (9),
представляет сумму двух экспонент
Пример 3:
Это учебный пример оптимального управления. Рассмотрим вертикальный спуск космического аппарата на поверхность планеты. Первое соотношение (11) есть цель управления, заключающаяся в минимальном затрате топлива
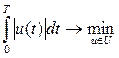 ; (11)
; (11)
где u(t) -расход топлива.
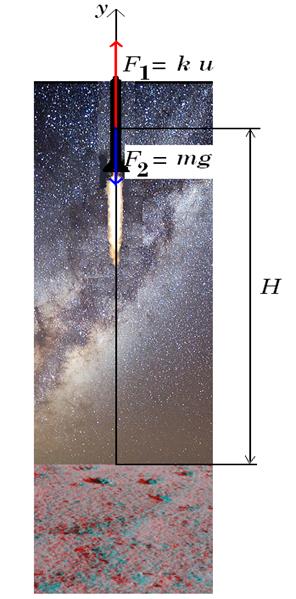
Вводя систему координат yОx , рис. 3 запишем дифференциальное уравнение движения, отражающего второй закон Ньютона
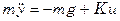 (12)
(12)
Дифференциальное уравнение замыкается краевыми условиями:
в начале движения
 ,
,  (13)
(13)
при завершении посадки.
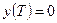
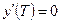
(14)
Лекция 2.
Основная задача ВИ
Пусть поставлена задача на минимизацию функционала J
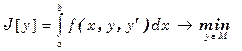 , (1)
, (1)
y(a)=y0 , y(b)=y1 , (2)
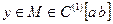 – область определения.
– область определения.
Сформулированную задачу называют простейшей задачей вариационного исчисления. Именно на этой задаче отрабатывались основные приемы решения этой дисциплины.
Вариация и её свойства.
Методы решения вариационных задач весьма напоминают методы исследования функций в математическом анализе. Поэтому введение новых понятий будет проводиться с параллельным напоминанием соответствующих понятий в математическом анализе.
1.Область определения
А)Область определения функции f(x) есть множество D вещественных чисел 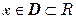 , при которых она имеет смысл (задана)
, при которых она имеет смысл (задана)
Б)Область определения функционала J(y) есть класс функций 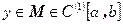 вещественной переменной, при которых он имеет смысл
вещественной переменной, при которых он имеет смысл
Область значений
А)Область значений функции 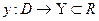 есть множество Y вещественных чисел, которые принимает функция, когда переменная x пробегает всю область определения
есть множество Y вещественных чисел, которые принимает функция, когда переменная x пробегает всю область определения 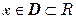 .
.
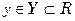 - область значений Y.
- область значений Y.
Б)Область значений функционала  есть множество Y вещественных чисел, которые принимает функционал, когда аргумент y(x) пробегает всю область определения
есть множество Y вещественных чисел, которые принимает функционал, когда аргумент y(x) пробегает всю область определения 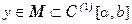 .
.
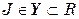 , область значений Y.
, область значений Y.
Приращение аргумента
А)Приращение аргумента называется переменная 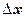 равная разности переменой x и фиксированной точки x0
равная разности переменой x и фиксированной точки x0
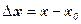
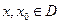 .
.
Дифференциал аргумента равен приращению
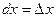
Например: 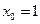
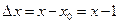 .
.
Б)Приращение (вариацией) аргумента функционала 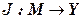 называется переменная
называется переменная 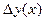 , равная разности между переменной y(x) и фиксированной функцией y0(x)
, равная разности между переменной y(x) и фиксированной функцией y0(x)
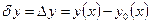 ,
, 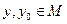 ,
, 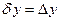 , (2б)
, (2б)
Например: 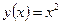 ,
, 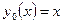 , тогда
, тогда
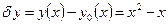 .
.
Вариация аргумента функционала есть в терминах математического анализа дифференциал функционала.
Непрерывность функционала
А)Если ( 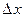 – мало
– мало 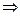
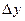 – мало), то
– мало), то  – непрерывно в
– непрерывно в
Более точное определение на языке эпсилон -дельта
Если 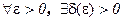 ,
, 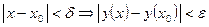 ,то
,то 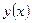 – непрерывна в точке
– непрерывна в точке 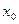 .
.
Б)Если (  – «мало»
– «мало»  – мало), то J непрерывно в точке y0
– мало), то J непрерывно в точке y0
На языке эпсилон-дельта
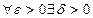 ;
;  , то
, то 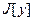 - непрерывна в точке y0.
- непрерывна в точке y0.
Замечание 1:
В вариационном исчислении утвердилась терминология функционального анализа вся функция называется точкой :  точка,
точка,  - точка.
- точка.
Замечание 2:
Понятие 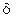 - окрестности нуждается в уточнении.
- окрестности нуждается в уточнении.
Экстремум
А)Если в некоторой окрестности 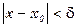 точки x0 аргумента выполняется
точки x0 аргумента выполняется 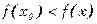 ,
, 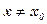 , то точка
, то точка 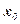 называется точкой минимума.
называется точкой минимума.
Б) Если в некоторой окрестности 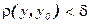 точки y0 аргумента выполняется
точки y0 аргумента выполняется 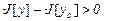 , то
, то 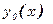 - точка локального минимума.
- точка локального минимума.
Близость кривых.
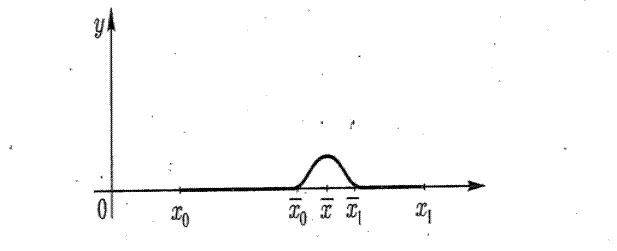
Близость кривых в смысле близости 0-го порядка.
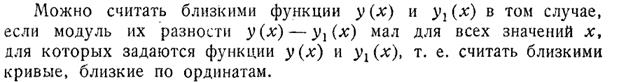
Пусть 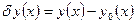 ,
, 
Определение. сли  – мало, то непрерывные функции
– мало, то непрерывные функции 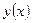 ;
; 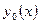 ; называются близкими в смысле близости 0 -го порядка.
; называются близкими в смысле близости 0 -го порядка.
Множество всех непрерывных функций 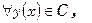 удовлетворяющих неравенству
удовлетворяющих неравенству 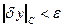 называется сильной e-окрестностью точки y0 и обозначается -
называется сильной e-окрестностью точки y0 и обозначается - 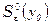
Пусть  ,
, 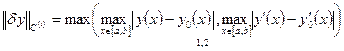 .
.
Определение.
Если 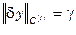 – мало, то непрерывно-дифференцируемые функции
– мало, то непрерывно-дифференцируемые функции 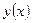 и
и 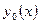 называются близкими в смысле близости 1 -го порядка.
называются близкими в смысле близости 1 -го порядка.
Множество всех непрерывно-дифференцируемых функций 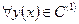 , удовлетворяющих неравенству
, удовлетворяющих неравенству 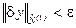 называется слабой e-окрестностью 1-го порядка точки y0 и обозначается –
называется слабой e-окрестностью 1-го порядка точки y0 и обозначается – 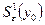
Теорема:
Если 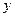 и
и 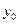 близки в смысле близости 1-ого порядка, то они близки и в смысле 0 порядка.
близки в смысле близости 1-ого порядка, то они близки и в смысле 0 порядка.
Доказательство:
 ;
;  ,
,
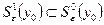 ,
, 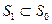 .
.
ч.т.д.
Лекция 3
Уравнение Эйлера
Исследуем на экстремум функционал
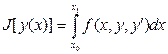 (1)
(1)
где  трижды непрерывная функция по всем аргументам.
трижды непрерывная функция по всем аргументам.
Краевые условия
 ,
, 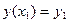 (2)
(2)
Необходимое условие экстремума
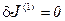 (3)
(3)
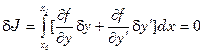
 ,
,  (4)
(4)
Интегрируя по частям,  учитывая
учитывая
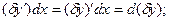
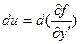 =
= 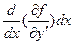 ;
;
получим
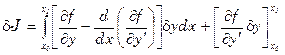 =0; (6)
=0; (6)
Или учитывая (4)
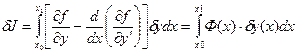
Основная лемма вариационного исчисления
Теорема: Если для каждой непрерывной функции 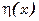 следующий функционал равен нулю
следующий функционал равен нулю

Где функция 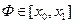 непрерывна на отрезке, то
непрерывна на отрезке, то
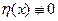
 (1)
(1)
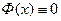 на том же отрезке.
на том же отрезке.
Доказательство. (2)
Пусть 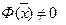 в некоторой точке
в некоторой точке  . В силу её непрерывности она сохраняет знак и в некоторой окпестности точки. , но тогда выбпрая произвольно и функцию
. В силу её непрерывности она сохраняет знак и в некоторой окпестности точки. , но тогда выбпрая произвольно и функцию 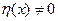 сохраняюшую знак на
сохраняюшую знак на 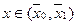 этой окрестности и равной нулю
этой окрестности и равной нулю 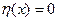 при
при 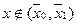 в других точках отрезка, получим
в других точках отрезка, получим
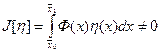 , что противоречит условию теоремы. Следовательно, предположение том, что функция не равна нулю хотя бы в одной точке отрезка, неверно и
, что противоречит условию теоремы. Следовательно, предположение том, что функция не равна нулю хотя бы в одной точке отрезка, неверно и 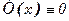 в любой точке отрезка.
в любой точке отрезка.
Применяя основную теорему вариационного исчисления к равенству

получим (7а)
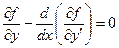
Или беря полную производную получим
 (7б)
(7б)
Это уравнение и называется уравнением Эйлера.
Примеры:
1) 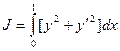 ,
, 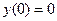 ,
, 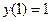
Применяя уравнение Эйлера получим дифференциальное уравнение второго порядка
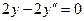
Записываем характеристическое уравнение
 и находя корни
и находя корни 
Получим общее решение дифференциального уравнения
 ,
,
Используя граничные условия получим частное решение
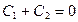 ,
, 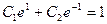 ,
, 

Это и есть экстремаль. Экстремум функционала может достигаться толко на этой кривой.
2) 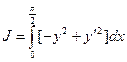 ,
, 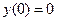 ,
, 
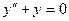 ,
, 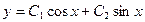 ,
, 
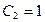
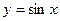
3)  ,
, 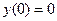 ,
, 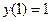
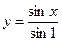
4) 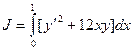 ,
, 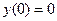 ,
, 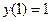
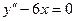 ,
,  ,
, 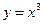
Частные случаи функционала
Пусть дан функционал

Заданы краевые условия
 ,
, 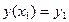
Рассмотрим частные случаи вида функции  интегрируемости уравнения Эйлера.
интегрируемости уравнения Эйлера.
1) 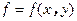 - подынтегральная функция не зависит от производной
- подынтегральная функция не зависит от производной 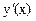
Уравнение Эйлера имеет вид
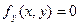
Это есть алгебраическое уравнение, не содержащее произвола и поэтому не удовлетворяющее в общем случае граничным условиям. Решения, вообще говоря, не существует.
Пример:
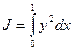 ;
;  ,
, 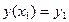
Уравнение Эйлера
 ;
; 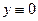 ;
;
2) Функция f линейно зависит от производной
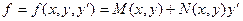
Тогда уравнение Эйлера имеет вид
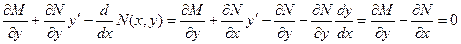
Но это опять алгебраическое уравнение.
Здесь можно различить два случая
а) 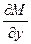 =
=  -алгебраическое уравнение
-алгебраическое уравнение
б)  -тождество, тогда функционал есть полный дифференциал и его значение не зависит от на допустимых кривых. Вариационная задача теряет смысл.
-тождество, тогда функционал есть полный дифференциал и его значение не зависит от на допустимых кривых. Вариационная задача теряет смысл.
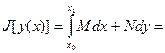

Примеры:
а) 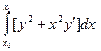 ,
, 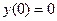 ,
, 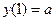
Решение
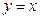
Первое граничное условие удовлетворяется, а второе только при a = 1
б)  ,
,
Уравнение Эйлера превращается в тождество. Значение функционала не зависит от пути интегрирования.
3)
Функция зависит только от производной
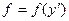
Общее уравнение Эйлера имеет вид 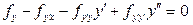
принимает вид
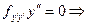
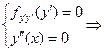

Все решения прямые.
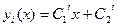
Пример:
а) Найти кривую, соединяющую две точки и имеющую наименьшую длину.
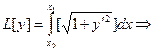

б) Задача брахистохроны, имеющей скорость зависящую от производной
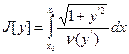 с.36.
с.36.
4) Подынтегральная функция не зависит от y.



Уравнение Эйлера
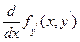

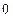
Имеет первый интеграл
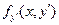

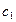
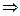



Пример. Пусть знаменатель в задаче о брахистохроне равен x. Это означает что скорость скатывания пропорциональна координате x.
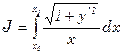
Первый интеграл
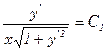
Первый способ решения



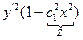 =
= 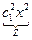
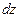

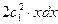
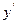


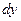

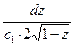
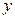




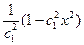

 ;
; 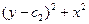
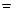
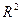

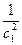
Второй способ решения.
Введём параметр

Тогда
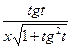


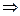
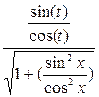

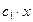
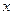

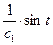

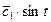
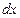


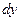

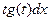

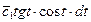


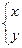

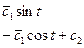
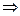
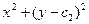



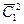
5) Пусть подынтегральная функция зависит от y и y’ и не зависит от x.
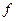

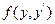



Если почтенно умножить уравнение на 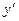 , прибавить и вычесть слагаемое
, прибавить и вычесть слагаемое  то нетрудно проверить, что получается полная производная
то нетрудно проверить, что получается полная производная
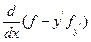

 .
.
Имеется первый интеграл.
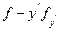 =
= 
5) Пример о наименьшей поверхности вращения.
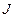 =
= 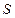 =
= 
Решение.
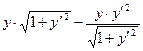 =
= 
 =
= 
Делаем подстановку
 =
= 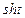 ,
,  =
= 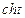 ,
, 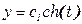 , где
, где  ,
,
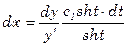 =
= 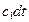 ,
,
 ,
,
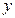 =
= 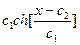 - цепная линия
- цепная линия
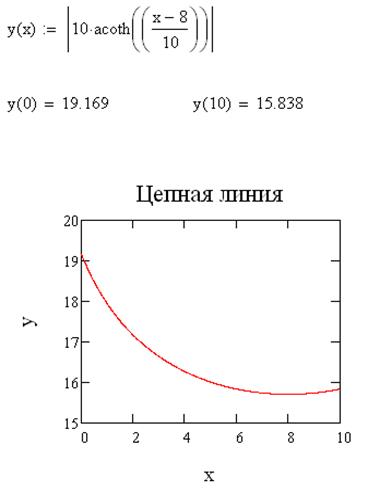
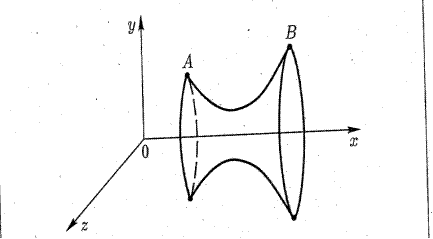
6) Задача о брахистохроне
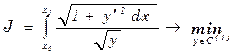

 =
= 
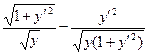 =
= 
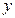 =
= 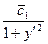 ;
; 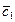 =
= 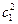
 =
=  ;
;
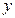 =
=  =
= 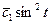 ;
;
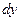 =
= 
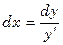
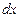 =
= 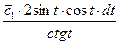 =
= 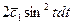
 =
=  =
= 
 =
= 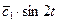 =
= 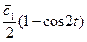
Задача Пуанкаре
История пятого постулата геометрии Евклида. Изложение упрощено.
Подробно см. Н.В. Ефимов “Высшая геометрия”. Наука . 2002. 575 с.
Евклид, жил приблизительно от 330 до 275 года до нашей эры. Составленные им начала содержат 8 определений, 5 постулатов и 9 аксиом.
Определения.
1.Точка есть то, что не имеет частей.
2.Линия есть длина без ширины.
3.Границы линии суть точки.
4.Прямая есть линия одинаково расположенная ко всем своим точкам.
5.Плоскость есть то, что имеет только длину и ширину.
6.Границы поверхности есть линии.
7.Плоскость есть поверхность одинаково расположенная ко всем своим прямым.
8.Плоский угол есть взаимное наклонение двух встречающихся линий, расположенных в одной плоскости.
Далее следует список основные утверждения (постулаты и аксиомы)
С современной точки зрения нет разницы между постулатами и аксиомами и неясно, какой принцип имел в виду Евклид разбивая основные утверждения на два класса.
Постулаты
1.Через две точки проходит прямая и притом одна.
2.Каждую прямую можно неограниченно продолжить в обе стороны.
3.Из любой точки можно описать окружность любого радиуса.
4.Все прямые углы равны.
5. Если дана прямая и точка вне её, то через точку проходит прямая параллельная данной прямой и притом только одна.
Аксиомы
6.Равные порознь третьему тоже равны.
7.Если к равным прибавить равные, то и получим равные.
8.Если от равных отнимем равные, то и получим равные.
9.Если к неравным прибавим равные, то получим неравные.
10.Если удвоить равные, то получим равные
11.Половины равных равны.
12.Совмещающиеся движением равны.
13.Целое больше любой части.
14.Две прямые не могут заключать пространства.
С точки зрения современной геометрии изложение геометрии на основе 14 основных утверждений следует признать неудовлетворительным во многих отношениях. Прежде всего определения оперируют такими понятиями, которые сами должны быть определены: граница, длина, и т.д. и ни одно не используется при доказательстве каких либо теорем. Что же касается 14 первичных утверждений, то они в целом существенны, но слишком бедны для безукоризненного логического развертывания геометрии, потому что многие факты опираются на наглядность чертежа. Утверждение 5 выглядит как теорема, которую следовало бы доказать на основе 13 других утверждений. Возможно сам Евклид пытался доказать пятый постулат. До конца 19 столетия было предложено много доказательств 5 постулата, но все они оказались ошибочными. Если бы собрать все труды, посвящённые 5 постулату, то они составили бы большую библиотеку.
Из многочисленных работ посвящённых проблеме 5 постулата следует выделить работы Саккери 1733 и Ламберта 1766. В результате их работ появилось гипотеза о том, что 5 постулат не может быть доказано на основе других 13. Ламберт далее, кто либо до него шел по правильному пути и видимо предчувствовал правильное решение проблемы. Ламберт писал: “Доказательство 5 постулата может быть доведено столь далеко, что остаётся по видимому ничтожная мелочь. Но при тщательном рассмотрении оказывается, что в этой мелочи как раз и содержится вся суть вопроса: обыкновенно она содержит равносильное 5 постулату утверждение и получается порочный логический круг. Я думаю, что все попытки доказательства 5 постулата невозможны.” Значительный вклад в раскрытие истинного смысла 5 постулата внесли также Лежандр, Швейкарт, Тауринус. Однако истинный смысл этого постулата был понят только Гауссом, Больяи и Лобачевским. Причем Лобачевскому принадлежит приоритет наиболее полного освещения проблемы в открытой печати. Если неевклидову геометрии сравнить с огромным деревом, то исследования Гаусса относятся к корням этого дерева, исследования Больяи - к ветвям, а Лобачевского ко всему дереву в целом. История этих исследований черезвычайна поучительна, однако суть может быть выражена в немногих словах.
Анализируя многовековые попытки доказательства 5 постулата, Лобачевский делает гипотезу, о его недоказуемости на основе остальных 13 утверждений. Далее Лобачевский делает вывод, раз нельзя доказать 5 постулат, то заменив его другим утверждением, противоположным утверждением, можно построить другую геометрию.
Аксиома Лобачевского формулируется так:
Через точку, вне данной прямой на плоскости, можно провести более одной прямой, не пересекающую данную прямую.
Появляются понятия непересекающихся и параллельных прямых. В Евклидовой геометрии есть только параллельные прямые.



Введение этих отличий не так просто и поэтому долгое время геометрию Лобачевского мало кто принимал. Из рисунка видно, что через точку вне прямой проходит три класса прямых:  правая и
правая и  левая - параллельные прямые,
левая - параллельные прямые,  - непересекающиеся прямые,
- непересекающиеся прямые, 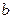 - пересекающиеся прямые. Однако модельные построения сыграли огромную роль в наглядном отображении сути всех абстрактных логических построений Лобачевского.
- пересекающиеся прямые. Однако модельные построения сыграли огромную роль в наглядном отображении сути всех абстрактных логических построений Лобачевского.
§11.Модель Пуанкаре и неевклидова геометрия Лобачевского.
Согласно принципу Ферма путь светового луча, распространяющегося в неоднородной среде является экстремалью вариационной задачи
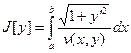
Если скорость зависит только от y, то получим вариационную задачу
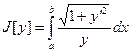
Поскольку подынтегральная функция не содержит явно x , то запишем первый интеграл
 =
= 
После упрощений получим
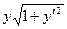 =
=  =
= 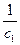
Решаем дифференциальное уравнение
 =
= 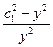
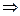
 =
= 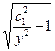
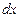 =
=  ;
; 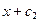 =
= 
Получаем общее решение зависящее от двух констант.
 =
= 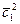 =
= 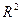
Это окружности центр которых находится на оси x. Через две любые точки верхней полуплоскости проходит единственная экстремаль q.
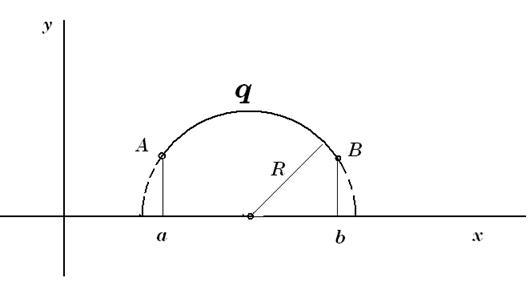
Оптической длиной кривой q( x) назовется значение интеграла 
Будем рассматривать верхнюю плоскость как оптическую среду в которой скорость света v в каждой точке равна ординате  . Лучами света в этой среде будут полуокружности. Если одна или обе точки А и В лежат на оси x , то значение оптической длины экстремали будет равна бесконечности.
. Лучами света в этой среде будут полуокружности. Если одна или обе точки А и В лежат на оси x , то значение оптической длины экстремали будет равна бесконечности.

Модель Пуанкаре относится к большим расстояниям, вопазмерным размерам вселенной. Условный рисунок части вселенной. Скопления галактик и прямая между удалёнными точками..
Поэтому точки лежащие на оси Ох будем называть бесконечно удалёнными. Будем называть линии по которым распространяется свет (окружности на плоскости) прямыми, оптические длины экстремалей между точками А и В просто длинами. Две прямые могут пересекаться.
Две прямые имеющих общую бесконечно удалённую точку - параллельными прямыми. Легко видеть, что все утверждения Евклида справедливы на плоскости с такими прямыми, за исключением 5 постулата, вместо него дсправедлив постулат Лобачевского. 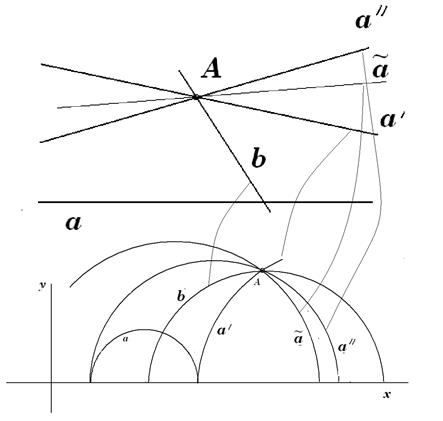
Через точку А вне прямой a проходят три класса прямых:  правая и
правая и  левая - параллельные прямые,
левая - параллельные прямые,  - непересекающиеся прямые,
- непересекающиеся прямые, 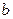 - пересекающиеся прямые. §12 Численные способы решения. Примеры задач.
- пересекающиеся прямые. §12 Численные способы решения. Примеры задач.
12. Численные методы
12.1. Метод стрельбы
Пусть дана вариационная задача
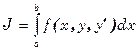 ;
; 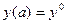 ;
; 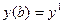
Уравнение Эйлера есть дифференциальное уравнение второго порядка.
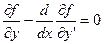
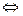
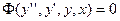
Разрешим его относительно второй производной, это часто можно сделать. Если нельзя, то алгоритм немного усложняется.
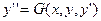
Граничные условия при
При
x=a :  ;
;
x=b: 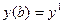
Общее решение зависит от 2 констант
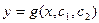
Корректность краевой задачи будет определяться возможность решения системы полученной из общего решения, при подстановке в нею граничных условий.

Заменим производные разделёнными разностями.
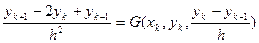
Тогда для интегрирования явным методом для получения значения функции в новой точке необходимо знание значений в двух предыдущих
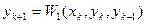
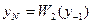 ;
; 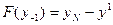
Пример:
Рассмотрим простой учебный пример

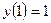
 (8)
(8)
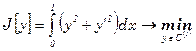 (9)
(9)
Полученное с помощью уравнения Эйлера решение рис.2 даётся равенством
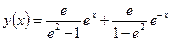
Сравнение с решением полученном числено показано на рис.

Второй пример
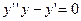

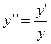
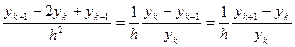
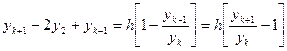
1. 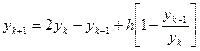
2. 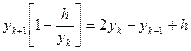 ;
; 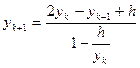
12.3.Метод Ньютона (конечных разностей).
Пусть дано уравнение Эйлера
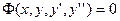

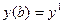
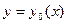
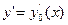
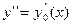
Разложим в ряд Тейлора
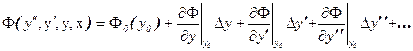
Требуется решить уравнение
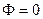
Ограничимся только 4 слагаемыми
Это линейное уравнение
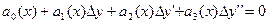
Задавая начальное нулевое приближение 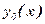
И решая дифференциальное уравнение с краевыми условиями
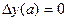 ,
, 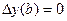 ,
,
 ,
, 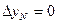 .
.
получим первое приближение
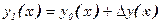
Пример:
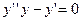
 ,
, 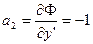 ,
, 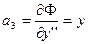 ;
;
 ,
,
Возьмём линейную функцию
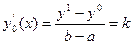 ,
,
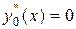 ,
,
Подставим в уравнение
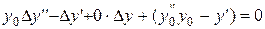
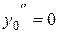 ,
, 
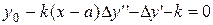
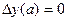 ;
; 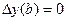

Получим разностную схему
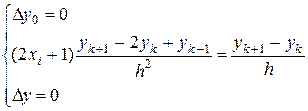 ,
, 
Это есть система линейных уравнений
Геодезические экстремали
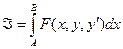 - есть
- есть  -длина кривой y(x).
-длина кривой y(x).
Если y(x) – экстремаль, то  - геодезическое расстояние
- геодезическое расстояние
 - окружность (геодезическая окружность)
- окружность (геодезическая окружность)
 - эллипс,
- эллипс, 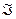 - гипербола
- гипербола
Пример:
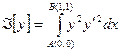
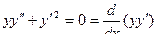
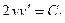

 ;
; 
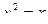

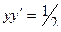

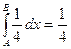 -
-  -длина
-длина
Пример:
Найти  - окружность в
- окружность в 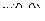 радиусе R
радиусе R
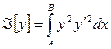
Из предыдущего:
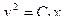
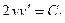

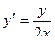
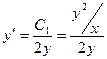
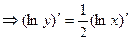
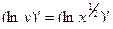





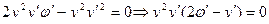
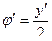

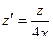
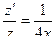

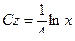
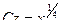
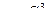

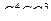
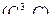 - лежит на окружности и на экстремали
- лежит на окружности и на экстремали
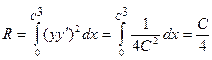


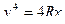
Пусть поверхность задана векторным уравнением

Геодезической линией называется линия наименьшей длины соединяющей две точки на поверхности.
Линия на поверхности

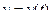
Её длина
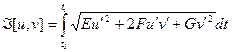
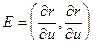


Уравнение Эйлера
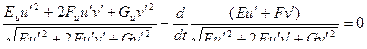
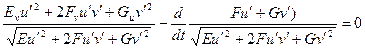
Пример:
Среди всех кривых на сфере R соединяющих две точки выделить те, которые имеют наименьшую длину.
 -долгота
-долгота 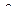 -широта
-широта


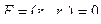
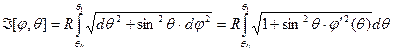
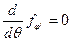
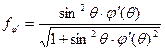

Объекты управления

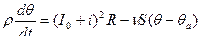



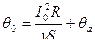
 =
= 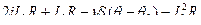
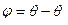
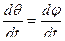
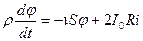
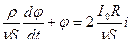

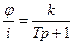
Уровень в бане
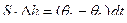

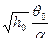


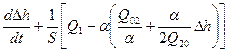 =
= 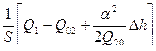

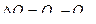
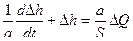
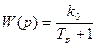
Преобразования Лапласа

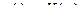

Регуляторы
П – пропорц.
ПИ – пропорц-интегр.
ПИД – пропорц-интегр-дифференц.


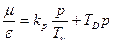
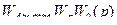
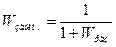
Вывод.
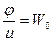
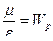
 =
= 
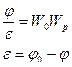


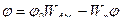

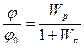
Задача: выбрать параметры 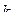 ,
,  ,
, 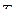 , чтобы обеспечить устойчивость и качество регулирования (переходного процесса).
, чтобы обеспечить устойчивость и качество регулирования (переходного процесса).

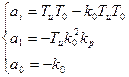
Критерий Рауса-Гурвица
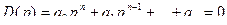

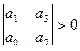
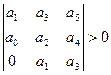 …
…
необх. и дост.. чтобы все определители имели знаки одинаковые со знаком первого коэффициента k-го уравнения.
Частотный критерий
Михайлов
Найквист
Если разомкнутая система является неустойчивой, то для того чтобы замкнутая система была устойчивой необходимо и достаточно, чтобы амплитудно-фазовые характеристики разомкнутой системы  при изменении
при изменении  от 0 до
от 0 до 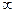 , охватывали точку
, охватывали точку 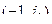 в положительном направлении
в положительном направлении 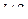 раз, где l число кривых k-го уравнения разомкнутой системы.
раз, где l число кривых k-го уравнения разомкнутой системы.
Михайлов
Для ого чтобы (замкнутая) система была устойчивой необх. и. дост. чтобы кривая Михайлова (гедограф) при изменении  от 0 до
от 0 до 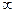 начинался
начинался 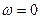 на вещественной положительной полуоси обходящей только против часовой стрелки последующие n-квадрантов n-порядок k-го уравнения.
на вещественной положительной полуоси обходящей только против часовой стрелки последующие n-квадрантов n-порядок k-го уравнения.
Постановка задачи оптимального управления
































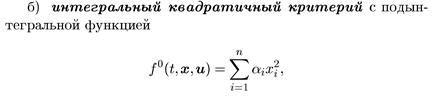

























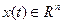
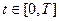
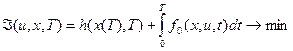

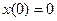
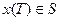
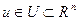
Множество конечных состояний S задается

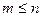

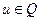
 - непрерывны по переменным x и y
- непрерывны по переменным x и y
Примеры объектов управления
Бак
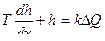
 ,
, 
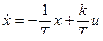
Печь нагревания

 ,
, 
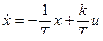
Управление космическим аппаратом



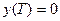
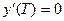
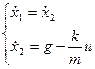

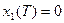


а) 
b) 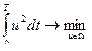
Пример:
 ;
;
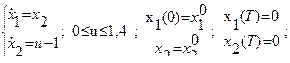
 ;
;
 ;
;
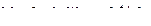 ;
;
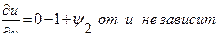
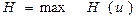

 ;
;
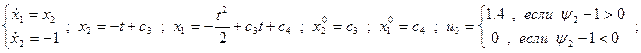
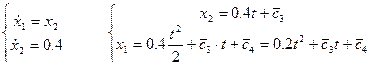 ;
;
Пример1:

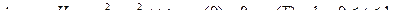

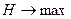 ;
;
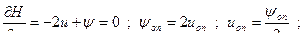


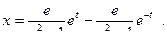
Пример 2:


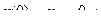

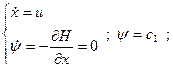
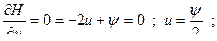
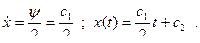
Доказательство принципа максимума
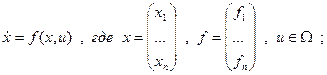
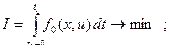

Сведём задачу к задаче … :
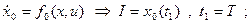
Перепишем задачу:
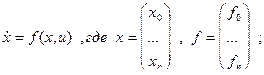
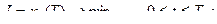

Найти xоп – оптимальный, uоп – оптимальный. Пусть 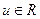 п – скалярное управление.
п – скалярное управление.
Допустим, что xоп и uоп найдены. Проварьируем управление на малом промежутке ε, изменив управление до величины u ≠ uоп ( игольчатая вариация ).
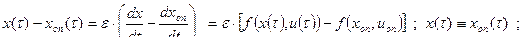
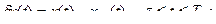
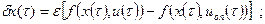
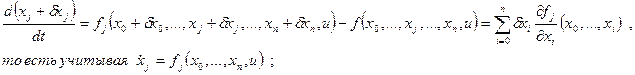
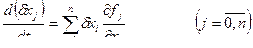

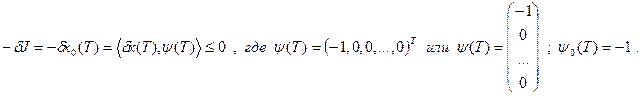
Поставим задачу получить ψ(T), который удовлетворил бы уравнению:
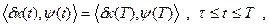
в частности, 
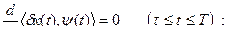
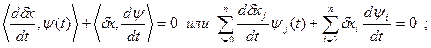

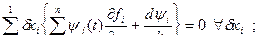
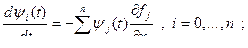


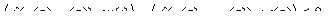
Обозначим 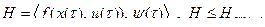
Отсюда следует, что Н достигает максимума при оптимальном  ,следовательно, надо выбирать
,следовательно, надо выбирать  так, чтобы Н достигала максимального значения.
так, чтобы Н достигала максимального значения.
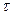 – произвольно ,
– произвольно , 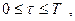 при n максимальном.
при n максимальном.
Численный метод решения задач оптимального управления.
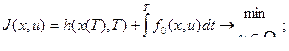
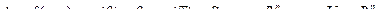
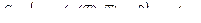
Краевая задача
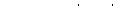
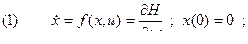
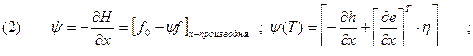

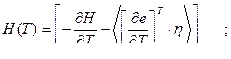

Метод стрельбы
 .
.
Задача Коши
Интегрируя (1) и (2) с некоторыми значениями  находят
находят  и определяют
и определяют 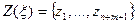 , где
, где
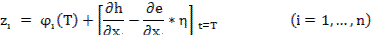
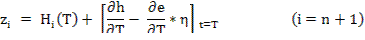
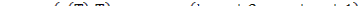
Численно используется метод Ньютона:
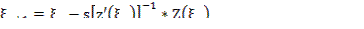
Или регуляризованный алгоритм:


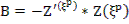
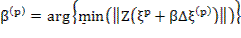

Z’ – матрица;
 - сумма невязок
- сумма невязок
α – параметр регуляризации;
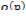 –параметр шага;
–параметр шага;
T – транспонированная матрица, Е – единичная матрица.
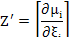
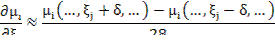
Задача о подъеме ракеты зонда
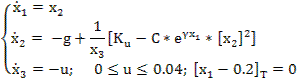
x1 – высота; х2 – скорость; х3 – переменная масса; К – коэффициент, характеризующий силу тяги;
g, c, γ – ускорение свободного падения, коэффициент аэродинамики сопротивления, коэффициент убывания плотности.
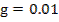 ;
;  ;
;  ;
; 
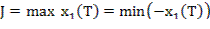
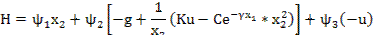
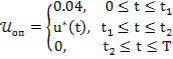 – скользящий равен
– скользящий равен 
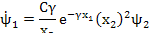
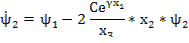
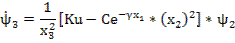
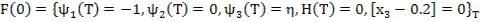
Задача о манёвре самолёта
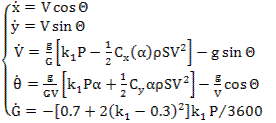 0.05
0.05 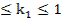
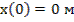
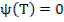

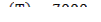


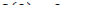
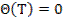
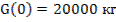

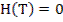
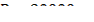 ;
;
 ;
;
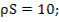

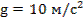
Метод решения:
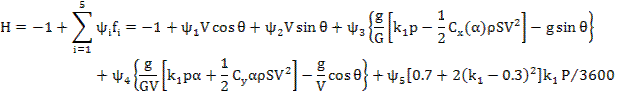
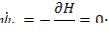
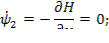

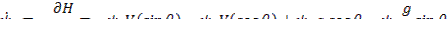

Задача о перелёте с орбиты Земли на орбиту Марса.
Задача 11.
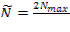 ;
;
N – мощность ракетной струи;
c – дополнительно установленная скорость отбр. шасси;
 ;
;
 ;
;
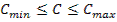
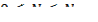
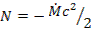 .
.
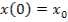 ;
;
 ;
;
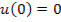 ;
;
 .
.

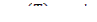

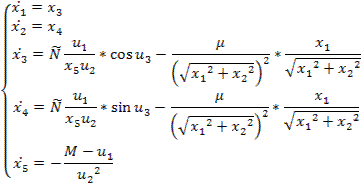

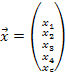
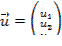
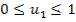


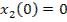


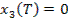

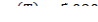
Оптимальное планирование поставок продукции.
Пример:
(1) 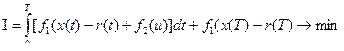
(2) 
(3) 
Решим задачу с помощью принципа max. Составим функцию Понтрягина:
(4) 
Записываем систему дифференциальных уравнений:

(5)
(6)
(7) 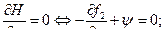
(8) 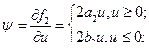
Из этого уравнения выразим уравнением через 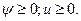
(9) 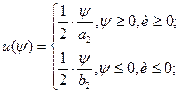
Подставим u(ψ) в (5):
(10) 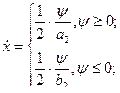
Краевое условие найдем продифференцировав 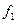 по
по 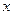 (T):
(T):
(11) 

 (12)
(12) 
Метод стрельбы для решения краевой задачи.
а) способ интегрирования.

(13)
(14)
 (15)
(15) 
(16)
Алгоритм. Задаем ψ0. Произвольно x0. Вычисляем по формулам (15), (16) x1,ψ1  x2,ψ2
x2,ψ2  …
…  x(T), ψ(T).
x(T), ψ(T).
В силу (122):
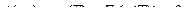 или
или 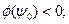
Задача о об оптимальноё поставке продукции
Пример:
(1) 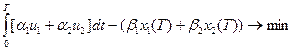
(2)  ;
; 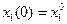 ;
;
(3) 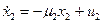 ;
;  ;
;
(4) 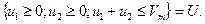
Формула функции Понтрягина:
(5) 
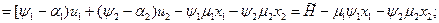

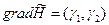
Согласно принципу max  (
(  → max) :
→ max) :
u1=0 u2=0 
u1=Vm u2=0 
u1=0 u2=Vm 
Составляем сопряженную систему:

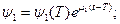
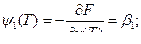
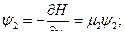
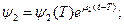
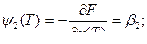
Получим зависимость 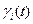 :
:



Итак получим  и можем вычислить значения функционала
и можем вычислить значения функционала  .
.
Задача об оптимальном управлении отраслью
Пример :
(1) 
(2) 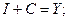
(3) 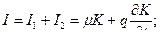
(4) 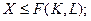
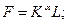
(5) 
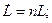
(6) 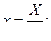

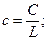
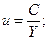

 ;
;
(7) 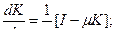
(8) из (2) 
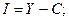

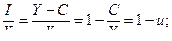
(9) из (1) 


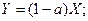
(10) из (8) и (9) 
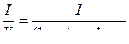

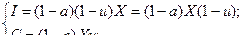
(11) из (7) и (10) 

(12) из (11) и (4) 
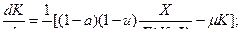
(13) из (11) и (6) 
 =
=
= 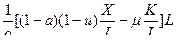 =
= 
(14) из (13) и (5) 

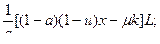

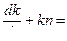
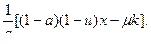
(15) Пусть q=1, тогда из (14) 
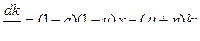
(16) из (4) и (6) 


 , т.к.
, т.к. 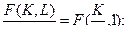
Предположим, что 
(17) 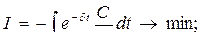
(18) 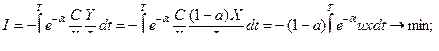
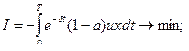

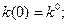

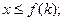
Механическая модель экономической задачи.
(1) 

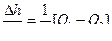

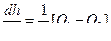 ;
;
(2) 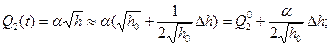
(3) из (1) и (2) 

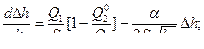
Обозначим 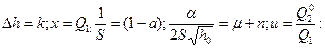
 совпадает с (15).
совпадает с (15).
Задача об оптимальном выпуске продукции
Пример:
(1) 
(2) 
(3) 

(4) 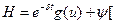
 ];
];
(**)(5) 
(6) 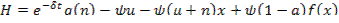

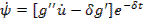
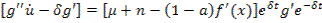
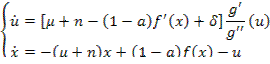
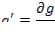
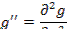
Пример 12.
Динамическая модель макроэкономической системы.
Введем следующие обозначения:
а – коэффициент производственного потребления  ;
;
μ – коэффициент амортизации;
n – темп роста трудовых ресурсов;
q – параметр модели;
ws – природные ресурсы;
u – доля потребления;
k – производственные финансы (основные);
X – валовый продукт;
Y – конечный продукт;
W – производственное потребление;
С – непроизводственное потребление;
I – капиталовложение;
I1 – амортизация отч?;
I2 – чистое капиталовложение;
F – производственная функция.
(1)  (1а)
(1а)
(2)  (2а)
(2а)
(3) 
(4) 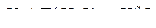
(5)  (5а)
(5а)
(6) 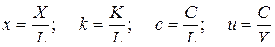
(7) 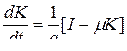

(8) из (2а): 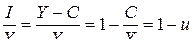
(9) из (1),(1а): 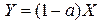

(10) из (8),(9): 
(11) из (7),(10): 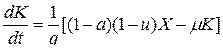

(12) из (4),(11): 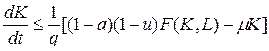
(13) из (6),(11): 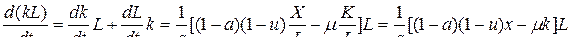
(14) из (5),(13): 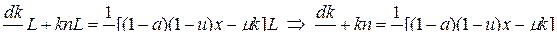
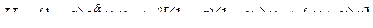

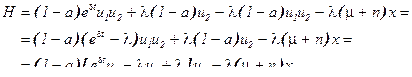

[1] Условие  (или
(или  ) часто называют усиленным условием Лежандра, а условием Лежандра называют неравенство
) часто называют усиленным условием Лежандра, а условием Лежандра называют неравенство 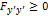 (или
(или 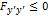 ).
).
Лекция 1
Задача о брахистохроне
В 1696 И.Бернулли опубликовал статью «О новой задаче к решению которой приглашаются математики». Это была задача о брахистохроне – задаче о линии быстрейшего спуска.

Задача.
Пусть заданы две точки А, В на плоскости и введена система координат (х,у). Требуется найти такую кривую (функцию) у(х), проходящую через А и В, так чтобы тяжелый шарик скатывался по этой кривой, без трения, достиг бы точки В за минимально возможное время.
Решение.
Решение задачи о брахистохроне было дано И. Бернулли, Я. Бернулли, Г. Лейбницем, И. Ньютоном и Г. Лопиталем. Линией быстрейшего ската не будет прямая, соединяющая точки А и В, хотя она и является кратчайшим расстоянием между точками А и В, так как при движении по прямой скорость движения будет нарастать сравнительно медленно, если же взять кривую, более круто спускающуюся около точки А вниз, то хотя путь и удлинится, но значительная часть пути будет пройдена с большей скоростью. Оказалось, что линией быстрейшего ската, является циклоида (брахистохрона).
Предположим, что начальная скорость скатывающейся точки равна нулю Воспользуемся законом сохранения. К моменту когда точка будет иметь координату y(x) рис.1 потенциальная энергия шарика уменьшится на величину mg·y, а кинетическая увеличится на величину mV2/2. В силу закона сохранения должно выполняться равенство:
 , (1)
, (1)
откуда
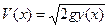 . (2)
. (2)
Дифференциал пути
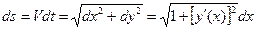 . (3)
. (3)
Дифференциал времени учитывая (2) и (3) равен
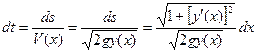 . (4)
. (4)
Беря определённый интеграл получим
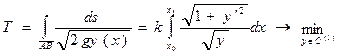 ,
, 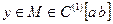 . (5)
. (5)
который дополняется краевыми условиями прохождения кривой через точки А и В
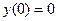 ,
, 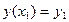 (6a,b)
(6a,b)
Решением вариационной задачи являются кривая, описываемая формулами
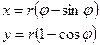 (7а, б)
(7а, б)
Формулы описывают траекторию точки на ободе колеса [ Справочник ]
Рассмотрим задачу со следующими условиями:
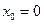
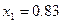 м.
м.

 м.
м.
Численно находится r и 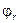
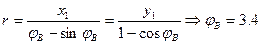 рад.
рад. 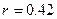 м.
м.
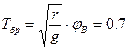 с.
с.
Время движения по наклонной плоскости равно.
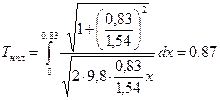 с
с
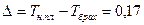 с
с

Рис.1. Линия быстрейшего спуска.
Пример 2:
Рассмотрим простой учебный пример
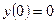
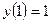
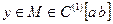 (8)
(8)
 (9)
(9)
Полученное с помощью уравнения Эйлера решение рис.2 даётся равенством
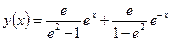 (10)
(10)

Рис.2. Экстремаль для функционала (9),
представляет сумму двух экспонент
Пример 3:
Это учебный пример оптимального управления. Рассмотрим вертикальный спуск космического аппарата на поверхность планеты. Первое соотношение (11) есть цель управления, заключающаяся в минимальном затрате топлива
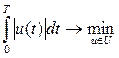 ; (11)
; (11)
где u(t) -расход топлива.

Вводя систему координат yОx , рис. 3 запишем дифференциальное уравнение движения, отражающего второй закон Ньютона
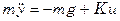 (12)
(12)
Дифференциальное уравнение замыкается краевыми условиями:
в начале движения
 ,
,  (13)
(13)
при завершении посадки.
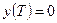
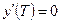
(14)
Сведение вариационной задачи к задаче конечномерной оптимизации
Рассмотри простую задачу вариационного исчисления
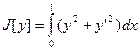 (1)
(1)
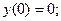
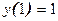 (2)
(2)
 - вектор является неизвестным (3)
- вектор является неизвестным (3)
Производные в трёх точках аппроксимируется разностными формулами
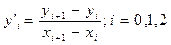 (4)
(4)
Между точками кривая аппроксимируется линейными функциями
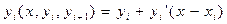 , i=0, 1, 2 (5)
, i=0, 1, 2 (5)
Подставляя формулы в интеграл получим задачу минимизации функции двух переменных
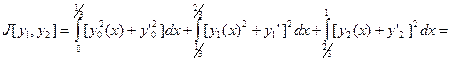 (6)
(6)  ;
;
Увеличивая количество точек, получим задачу на минимум от n переменных
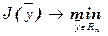 ;
;
 (7)
(7)
Следующие формулы демонстрируют переход от конечномерных задач оптимизации к бесконечномерным задачам вариационного исчисления:
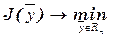 (8)
(8)
n=1 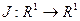 (9)
(9)
n=2 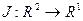
n=3 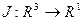
………………………..
n= 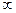
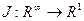 (10)
(10)
Лекция 2.
Основная задача ВИ
Пусть поставлена задача на минимизацию функционала J
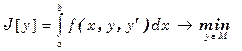 , (1)
, (1)
y(a)=y0 , y(b)=y1 , (2)
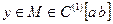 – область определения.
– область определения.
Сформулированную задачу называют простейшей задачей вариационного исчисления. Именно на этой задаче отрабатывались основные приемы решения этой дисциплины.
Вариация и её свойства.
Методы решения вариационных задач весьма напоминают методы исследования функций в математическом анализе. Поэтому введение новых понятий будет проводиться с параллельным напоминанием соответствующих понятий в математическом анализе.
1.Область определения
А)Область определения функции f(x) есть множество D вещественных чисел 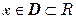 , при которых она имеет смысл (задана)
, при которых она имеет смысл (задана)
Б)Область определения функционала J(y) есть класс функций 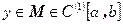 вещественной переменной, при которых он имеет смысл
вещественной переменной, при которых он имеет смысл
Область значений
А)Область значений функции 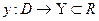 есть множество Y вещественных чисел, которые принимает функция, когда переменная x пробегает всю область определения
есть множество Y вещественных чисел, которые принимает функция, когда переменная x пробегает всю область определения 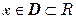 .
.
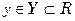 - область значений Y.
- область значений Y.
Б)Область значений функционала  есть множество Y вещественных чисел, которые принимает функционал, когда аргумент y(x) пробегает всю область определения
есть множество Y вещественных чисел, которые принимает функционал, когда аргумент y(x) пробегает всю область определения 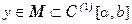 .
.
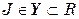 , область значений Y.
, область значений Y.
Приращение аргумента
А)Приращение аргумента называется переменная 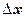 равная разности переменой x и фиксированной точки x0
равная разности переменой x и фиксированной точки x0
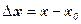
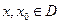 .
.
Дифференциал аргумента равен приращению
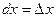
Например: 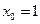
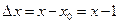 .
.
Б)Приращение (вариацией) аргумента функционала 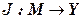 называется переменная
называется переменная 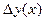 , равная разности между переменной y(x) и фиксированной функцией y0(x)
, равная разности между переменной y(x) и фиксированной функцией y0(x)
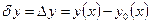 ,
, 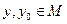 ,
, 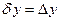 , (2б)
, (2б)
Например: 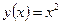 ,
, 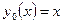 , тогда
, тогда
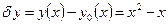 .
.
Вариация аргумента функционала есть в терминах математического анализа дифференциал функционала.
Непрерывность функционала
А)Если ( 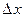 – мало
– мало 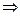
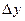 – мало), то
– мало), то 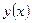 – непрерывно в
– непрерывно в
Более точное определение на языке эпсилон -дельта
Если 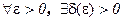 ,
, 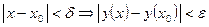 ,то
,то 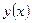 – непрерывна в точке
– непрерывна в точке 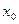 .
.
Б)Если (  – «мало»
– «мало»  – мало), то J непрерывно в точке y0
– мало), то J непрерывно в точке y0
На языке эпсилон-дельта
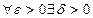 ;
;  , то
, то 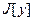 - непрерывна в точке y0.
- непрерывна в точке y0.
Замечание 1:
В вариационном исчислении утвердилась терминология функционального анализа вся функция называется точкой :  точка,
точка,  - точка.
- точка.
Замечание 2:
Понятие 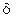 - окрестности нуждается в уточнении.
- окрестности нуждается в уточнении.
Экстремум
А)Если в некоторой окрестности 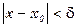 точки x0 аргумента выполняется
точки x0 аргумента выполняется 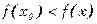 ,
, 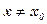 , то точка
, то точка 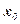 называется точкой минимума.
называется точкой минимума.
Б) Если в некоторой окрестности 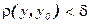 точки y0 аргумента выполняется
точки y0 аргумента выполняется 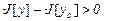 , то
, то 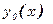 - точка локального минимума.
- точка локального минимума.
Близость кривых.
Близость кривых в смысле близости 0-го порядка.
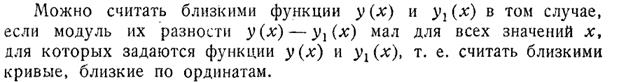
Пусть 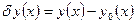 ,
, 
Определение. сли  – мало, то непрерывные функции
– мало, то непрерывные функции 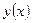 ;
; 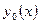 ; называются близкими в смысле близости 0 -го порядка.
; называются близкими в смысле близости 0 -го порядка.
Множество всех непрерывных функций 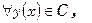 удовлетворяющих неравенству
удовлетворяющих неравенству 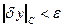 называется сильной e-окрестностью точки y0 и обозначается -
называется сильной e-окрестностью точки y0 и обозначается - 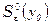
Пусть  ,
, 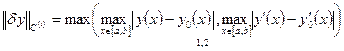 .
.
Определение.
Если 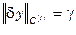 – мало, то непрерывно-дифференцируемые функции
– мало, то непрерывно-дифференцируемые функции 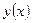 и
и 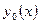 называются близкими в смысле близости 1 -го порядка.
называются близкими в смысле близости 1 -го порядка.
Множество всех непрерывно-дифференцируемых функций 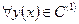 , удовлетворяющих неравенству
, удовлетворяющих неравенству 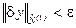 называется слабой e-окрестностью 1-го порядка точки y0 и обозначается –
называется слабой e-окрестностью 1-го порядка точки y0 и обозначается – 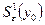
Теорема:
Если 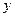 и
и 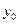 близки в смысле близости 1-ого порядка, то они близки и в смысле 0 порядка.
близки в смысле близости 1-ого порядка, то они близки и в смысле 0 порядка.
Доказательство:
 ;
;  ,
,
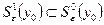 ,
, 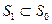 .
.
ч.т.д.
Лекция 3
Дата: 2018-11-18, просмотров: 393.