При вычислении определенного интеграла методом замены переменной (способом подстановки) определенный интеграл 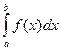 преобразуется с помощью подстановки
преобразуется с помощью подстановки 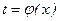 или
или 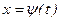 в определенный интеграл относительно новой переменной t. При этом старые пределы интегрирования a и b заменяются соответственно новыми пределами t1 и t2, которые находятся из исходной подстановки.
в определенный интеграл относительно новой переменной t. При этом старые пределы интегрирования a и b заменяются соответственно новыми пределами t1 и t2, которые находятся из исходной подстановки.
Из первой подстановки новые пределы интегрирования вычисляются непосредственно: 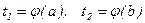 .
.
Из второй подстановки новые пределы интегрирования находятся путем решения уравнений 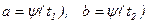 .
.
Таким образом, имеем
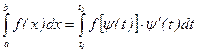
Пример 1: Вычислить определенный интеграл методом замены переменной 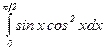
Решение: 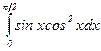 =
= 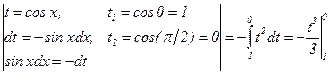
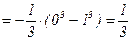 .
.
Пример 2: Вычислить определенный интеграл: 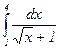 .
.
Решение: 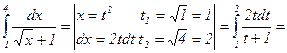
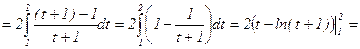
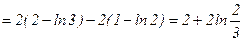 .
.
Вопросы для самопроверки по теме 3 Интегральное исчисление:
1. В чем заключается смысл действия, обратного дифференцированию?
2. Дать определение первообразной функции
3. Чем отличаются друг от друга любые две первообразные данной функции 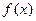 ?
?
4. Как проверить, правильно ли найдена первообразная данной функции 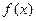 ?
?
5. Дать определение неопределенного интеграла.
6. Перечислить свойства неопределенного интеграла
7. Дать определение определенного интеграла.
8. Перечислить свойства определенного интеграла.
9. Запишите формулу Ньютона-Лейбница для вычисления определенного интеграла.
10. В чем отличия методов замены переменной в определенном и неопределенном интегралах?
Тема 4. Основы теории комплексных чисел
Рассмотрим уравнение вида: х2-4=0. Оно имеет действительные корни 2 и -2. Уравнение х2-4=0 действительных корней не имеет. Возникает необходимость введения новых чисел.
Определение 4.1.. Комплексными числами называют выражения вида а + bi, где а и b- действительные числа, а i - мнимая единица, причем i2=-1.
Алгебраическая форма комплексного числа.
Если 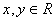 , то число
, то число 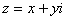 называется комплексным числом, заданным в алгебраической форме
называется комплексным числом, заданным в алгебраической форме
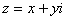 (2.3)
(2.3)
Это число имеет действительную часть 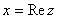
и мнимую часть 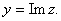
Так что 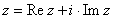
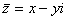 - число, сопряженное
- число, сопряженное 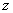 .
.
Пример:
Найти действительную и мнимую части комплексных чисел а)z 1=6-5i , б)z2= i.
Решение: а) 6 - действительная часть, -5 – мнимая часть;
б) 0 - действительная часть, 1 – мнимая часть.
Сумма комплексных чисел.
Определение 4.2. Суммой двух комплексных чисел а + bi и с + di будем называть комплексное число (а + c) + (b + d)i.
Определение 4.3. Произведением двух комплексных чисел а + bi и с + di будем называть комплексное число (ас - bd) + (ad + bc)i.
Пример:
Найти сумму и произведение комплексных чисел z 1=2-5i , z2= -7+i.
z 1 + z 2=(2 – 7) + (-5 + 1)i;
z *z 2=(-14 +5) +(2 + 35)i=-9 + 37i.
Модуль комплексного числа.
Определение 4.4.. Модулем комплексного числа z =а + bi называется число 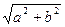 и обозначается
и обозначается 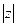 , т.е.
, т.е. 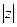 =
= 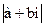 =
= 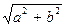 .
.
Пример:
Найти модуль комплексных чисел: а) 2-5i, б) -7+i.
Решение а) 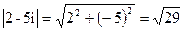 ;
;
б) 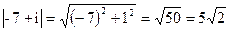 .
.
Дата: 2018-11-18, просмотров: 390.