Раздел I Линейная алгебра
Тема 1. Матрицы и определители
Определение 1.1. Матрицей называется прямоугольная таблица чисел.
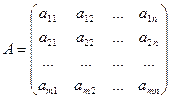
Обозначения: А – матрица, 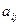 - элемент матрицы,
- элемент матрицы, 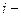 номер строки, в которой стоит данный элемент,
номер строки, в которой стоит данный элемент, 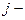 номер соответствующего столбца; m – число строк матрицы, n – число ее столбцов.
номер соответствующего столбца; m – число строк матрицы, n – число ее столбцов.
Определение 1.2. Числа m и n называются размерностями матрицы.
Определение 1.3. Матрица называется квадратной, если m = n. Число n в этом случае называют порядком квадратной матрицы.
Каждой квадратной матрице можно поставить в соответствие число, определяемое единственным образом с использованием всех элементов матрицы. Это число называется определителем.
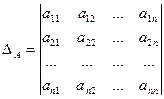
Определение 1.4. Определителем второго порядка называется число, полученное с помощью элементов квадратной матрицы 2-го порядка следующим образом:
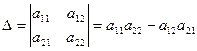 .
.
При этом из произведения элементов, стоящих на так называемой главной диагонали матрицы (идущей из левого верхнего в правый нижний угол) вычитается произведение элементов, находящихся на второй, или побочной, диагонали.
Примеры:
1. 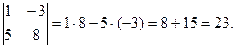 2.
2. 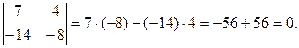
Определение 1.5. Определителем третьего порядка называется число, определяемое с помощью элементов квадратной матрицы 3-го порядка следующим образом:
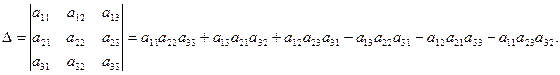
Замечание. Для того, чтобы легче запомнить эту формулу, можно использовать так называемое правило треугольников. Оно заключается в следующем: элементы, произведения которых входят в определитель со знаком «+», располагаются так:















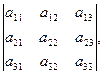 образуя два треугольника, симметричных относительно главной диагонали. Элементы, произведения которых входят в определитель со знаком «-», располагаются аналогичным образом относительно побочной диагонали:
образуя два треугольника, симметричных относительно главной диагонали. Элементы, произведения которых входят в определитель со знаком «-», располагаются аналогичным образом относительно побочной диагонали: 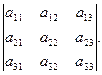
 Примеры.
Примеры.
1. 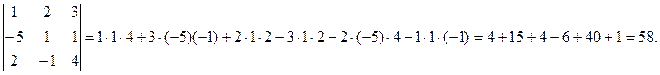
2. 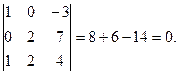
Определение1. 6. Транспонированием матрицы называется операция, в результате которой меняются местами строки и столбцы с сохранением порядка их следования. В результате получается матрица А`, называемая транспонированной по отношению к матрице А, элементы которой связаны с элементами А соотношением a` ij = aji .
Правило Крамера.
Рассмотрим систему (2.3). Назовем главным определителем этой системы определитель 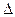 , элементами которого являются коэффициенты при неизвестных:
, элементами которого являются коэффициенты при неизвестных:
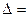
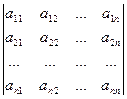 .
.
Предположим сначала, что 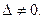 Умножим каждое уравнение системы (2.3) на алгебраические дополнения
Умножим каждое уравнение системы (2.3) на алгебраические дополнения 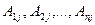 элементов j-го столбца
элементов j-го столбца 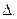
Сложив затем все уравнения, получим:
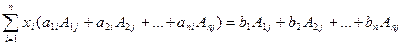 . (2.5)
. (2.5)
Отметим, что 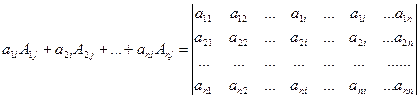 .
.
(j-й столбец)
(Результат получен из разложения определителя по j-му столбцу). Такой определитель равен 0 при 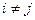 и равен
и равен 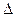 при i = j. Правая часть равенства (2.5) представляет собой определитель
при i = j. Правая часть равенства (2.5) представляет собой определитель 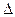 , в котором вместо j-го столбца стоит столбец свободных членов системы (2.3). Назовем такой определитель
, в котором вместо j-го столбца стоит столбец свободных членов системы (2.3). Назовем такой определитель 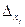 . Рассматривая j = 1,2,…, n, получим систему, эквивалентную исходной:
. Рассматривая j = 1,2,…, n, получим систему, эквивалентную исходной: 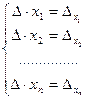 (2.6) . Разделив все уравнения на
(2.6) . Разделив все уравнения на 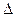 , найдем единственное решение:
, найдем единственное решение: 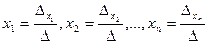 .
.
Предположим теперь, что 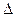 =0. Тогда система (2.6) примет вид:
=0. Тогда система (2.6) примет вид: 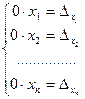 .
.
В этом случае, если все 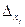 =0, система выглядит так:
=0, система выглядит так: 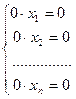 и имеет бесконечно много решений. Если же хотя бы один из
и имеет бесконечно много решений. Если же хотя бы один из 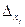
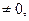 система решений не имеет.
система решений не имеет.
Таким образом, правило Крамера позволяет найти единственное решение системы (2.3) или сделать вывод о существовании бесконечного числа решений либо об их отсутствии:
1) Если 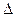
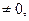 система (2.3) имеет единственное решение, определяемое по формулам:
система (2.3) имеет единственное решение, определяемое по формулам: 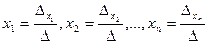 .
.
2) Если 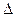 =
= 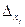 =0, система имеет бесконечно много решений.
=0, система имеет бесконечно много решений.
3) Если 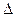 =0, а хотя бы один из
=0, а хотя бы один из 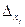
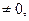 система не имеет решений.
система не имеет решений.
Примеры:
- Рассмотрим систему
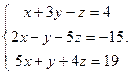 , решенную в предыдущем разделе методом Гаусса, и применим к ней правило Крамера. Найдем все нужные определители:
, решенную в предыдущем разделе методом Гаусса, и применим к ней правило Крамера. Найдем все нужные определители:
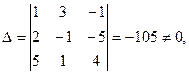 следовательно, система имеет единственное решение.
следовательно, система имеет единственное решение.
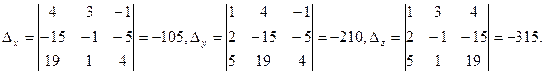
Отсюда 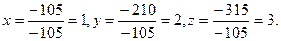
2. 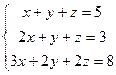 . Здесь
. Здесь 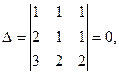 поскольку имеет два одинаковых столбца.
поскольку имеет два одинаковых столбца.
Следовательно, система не имеет единственного решения. Найдем 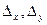 и
и 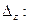
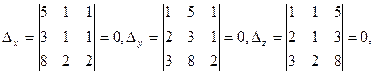 поэтому система имеет бесконечно много решений.
поэтому система имеет бесконечно много решений.
3. 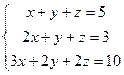 . Для этой системы
. Для этой системы 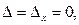 но
но 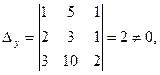
следовательно, решений нет.
Обратная матрица.
Определение 3.7. Квадратная матрица А называется вырожденной, если 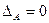 , и невырожденной, если
, и невырожденной, если 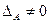 .
.
Определение 3.8. Квадратная матрица В называется обратной к квадратной матрице А того же порядка, если АВ = ВА = Е. При этом В обозначается 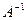 .
.
Рассмотрим условие существования матрицы, обратной к данной, и способ ее вычисления.
Теорема 3.2. Для существования обратной матрицы необходимо и достаточно, чтобы исходная матрица была невырожденной.
Замечание. Сформулируем еще раз способ вычисления обратной матрицы: ее элементами являются алгебраические дополнения к элементам транспонированной матрицы А, деленные на ее определитель.
Пример:
Найдем матрицу, обратную к 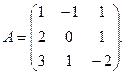
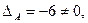 следовательно, матрица А невырожденная. Найдем алгебраические дополнения к ее элементам:
следовательно, матрица А невырожденная. Найдем алгебраические дополнения к ее элементам:
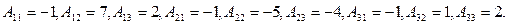 Не забудем, что алгебраические дополнения к элементам строки матрицы А образуют в обратной матрице столбец с тем же номером. Итак,
Не забудем, что алгебраические дополнения к элементам строки матрицы А образуют в обратной матрице столбец с тем же номером. Итак, 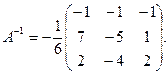 Можно убедиться, что найденная матрица действительно удовлетворяет определению
Можно убедиться, что найденная матрица действительно удовлетворяет определению 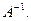 Найдем
Найдем
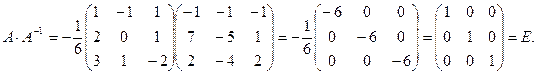
Тот же результат получим и при перемножении в обратном порядке.
Вопросы для самопроверки по разделу I Линейная алгебра
1. Что называется матрицей? Как определяются линейные операции над матрицами и каковы их свойства? Приведите примеры.
2. Что называется определителем? Каковы основные свойства определителей?
3. Что называется минором и алгебраическим дополнением? Приведите примеры.
4. Каковы способы вычисления определителей? Приведите примеры.
5. Что называется матрицей и расширенной матрицей системы линейных уравнений? Приведите примеры.
6. Что называется решением системы линейных уравнений? Какие системы называются совместными, а какие ¾ несовместными?
7. Сформулируйте теорему Кронекера-Капелли.
8. Напишите формулы Крамера. В каком случае они применимы?
9. При каком условии система линейных уравнений имеет единственное решение?
10. Что можно сказать о системе линейных уравнений, если ее определитель равен нулю?
11. При каком условии однородная система n линейных уравнений с n неизвестными имеет ненулевое решение?
12. Опишите метод Гаусса решения и исследования систем линейных уравнений.
13. Что называется рангом системы линейных уравнений? Как, используя метод Гаусса, можно найти ранг системы линейных уравнений?
14. Какие неизвестные в системе линейных уравнений и в каком случае называются свободными, а какие базисными? Что называется общим решением системы линейных уравнений?
15. Что называется рангом матрицы? Как его можно найти?
16. Что называется произведением двух матриц? Каковы свойства произведения матриц?
17. Какая матрица называется единичной?
18. Какая матрица называется обратной для данной матрицы? Всегда ли существует обратная матрица? Как можно найти обратную матрицу?
19. В чем состоит матричный способ решения систем линейных уравнений?
Основные теоремы о пределах
1. 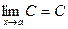
2. 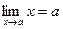
3. 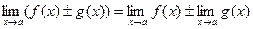
4. 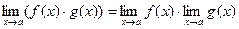
5. 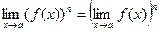
6. 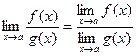
! Все правила имеют смысл, если пределы функций 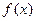 и
и 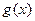 существуют.
существуют.
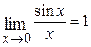 Используются также следующие пределы:
Используются также следующие пределы:
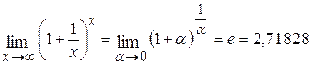
(первый замечательный предел);
(второй замечательный предел).
Техника вычисления пределов
При вычислении предела элементарной функции f(x) приходится сталкиваться с двумя существенно различными типами примеров.
· Функция f( x) определена в предельной точке x = a. Тогда
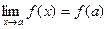 .
.
· Функция f(x) в предельной точке x = a не определена или же вычисляется предел функции при x→∞. Тогда вычисление предела требует в каждом случае индивидуального подхода.
Необходимо помнить, что
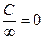 ,
, 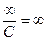 ,
, 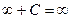 ,
, 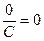 ,
, 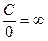 ,
, 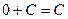 .
. 
Более сложными случаями нахождения предела являются такие, когда функция f(x) в точке x = a или при x→∞ представляет собой неопределенность (типа 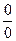 ,
, 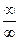 ,
, 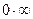 ,
, 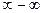 ,
, 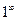 ,
, 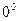 ,
, 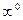 ).
).
При вычислении пределов при 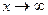 основные теоремы о пределах сохраняют силу и, кроме того, используются правила:
основные теоремы о пределах сохраняют силу и, кроме того, используются правила:
а) чтобы раскрыть неопределенность типа 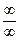 , необходимо числитель и знаменатель дроби разделить на наибольшую степень переменной;
, необходимо числитель и знаменатель дроби разделить на наибольшую степень переменной;
б) чтобы раскрыть неопределенность типа 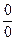 , необходимо числитель и знаменатель дроби разделить на наименьшую степень переменной ;
, необходимо числитель и знаменатель дроби разделить на наименьшую степень переменной ;
в) чтобы раскрыть неопределенность типа 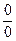 , иногда достаточно числить и знаменатель дроби разложить на множители и затем сократить дробь на множитель, приводящий к неопределенности;
, иногда достаточно числить и знаменатель дроби разложить на множители и затем сократить дробь на множитель, приводящий к неопределенности;
г) чтобы раскрыть неопределенность типа 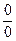 , зависящую от иррациональности, достаточно перевести иррациональность из числителя в знаменатель или из знаменателя в числитель и сократить на множитель, приводящий к неопределенности;
, зависящую от иррациональности, достаточно перевести иррациональность из числителя в знаменатель или из знаменателя в числитель и сократить на множитель, приводящий к неопределенности;
д) чтобы раскрыть неопределенность типа 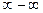 , необходимо числитель и знаменатель дроби одновременно умножить на сопряженное выражение и тем самым свести к неопределенности вида
, необходимо числитель и знаменатель дроби одновременно умножить на сопряженное выражение и тем самым свести к неопределенности вида 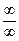 или
или 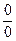 .
.
Вычислить пределы функций:
Пример 1: 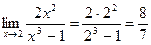
Пример 2: 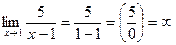
Пример 3: 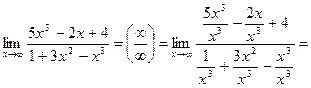
= 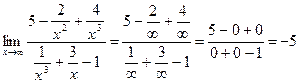
Пример 4: 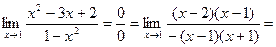
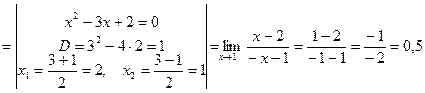
Пример5: 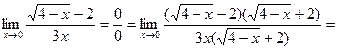
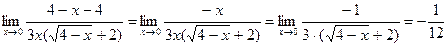
Пример 6:
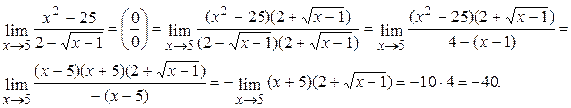
Пример 7:
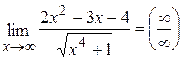 . Теорему о пределе частного здесь применить нельзя, так как числитель и знаменатель дроби конечного предела не имеют. В данном случае имеем неопределённость вида
. Теорему о пределе частного здесь применить нельзя, так как числитель и знаменатель дроби конечного предела не имеют. В данном случае имеем неопределённость вида 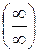 . Разделим числитель и знаменатель дроби на высшую степень х (в данном случае на х2 ), а затем воспользуемся теоремами о пределах функций:
. Разделим числитель и знаменатель дроби на высшую степень х (в данном случае на х2 ), а затем воспользуемся теоремами о пределах функций:
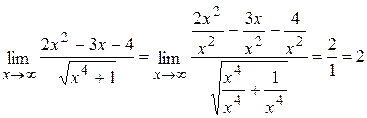 .
.
Здесь мы воспользовались следующим равенством: 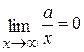 (а – любое число).
(а – любое число).
Пример 8:
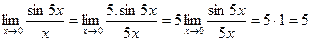
Пример 9:
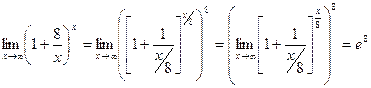
Пример 10:
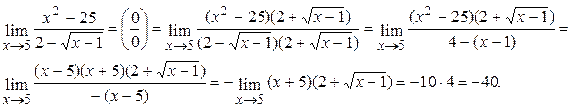
Вопросы для самопроверки по теме 1 Теория пределов:
1. Что называется функцией?
2. Что такое область определения и область значений функции
3. Перечислите способы задания функций, их достоинства.
4. Перечислите основные свойства функций.
5. Дайте определение предела функции в точке.
6. Какая функция называется непрерывной в точке?
7. Сформулируйте основные свойства пределов.
8. Как раскрывается неопределенность вида 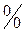 ,
, 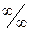 ?
?
Определение производной
Определение 2.1: Производной функции 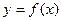 по аргументу x называется предел отношения ее приращения
по аргументу x называется предел отношения ее приращения 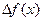 к приращению
к приращению 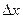 аргумента x, когда приращение аргумента стремится к нулю:
аргумента x, когда приращение аргумента стремится к нулю:
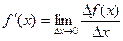 .
.
Если этот предел конечный, то функция y=f(x) называется дифференцируемой в точке x. Если же этот предел есть ∞, то говорят, что функция y=f(x) имеет в точке x бесконечную производную.
Механический смысл производной: скорость есть первая производная пути по времени, т.е. 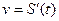 .
.
Геометрический смысл производной: тангенс угла наклона касательной к графику функции 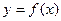 равен первой производной этой функции , вычисленной в точке касания, т.е.
равен первой производной этой функции , вычисленной в точке касания, т.е. 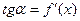
Уравнение касательной к графику функции 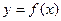 в точке
в точке 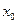 :
:
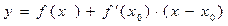
Уравнение нормали к графику функции 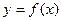 в точке
в точке 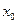 :
:
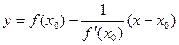
Таблица производных
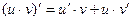
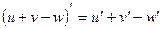
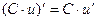
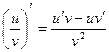
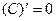
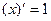
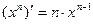
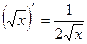
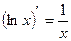
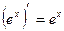
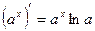
| 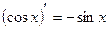
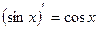
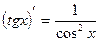
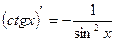
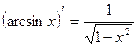
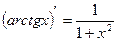
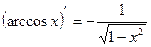
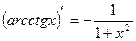
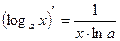
|
Процесс нахождения производных называется дифференцированием функции.
Найти производные функций:
Пример 1: 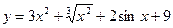
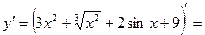
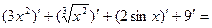
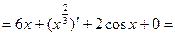
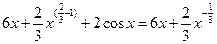 +
+
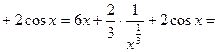
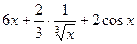
Пример2: 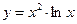
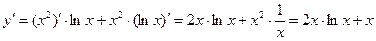
Пример 3: 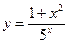
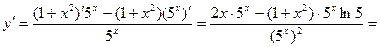
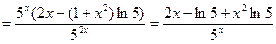
Производные высших порядков
Определение2.2: Производная второго порядка (вторая производная) от функции y=f(x) есть производная от ее первой производной: 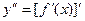 .
.
Определение 2.3 : Производная третьего порядка (третья производная) от функции y=f(x) есть производная от ее второй производной: 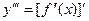 .
.
Определение 2.4 : Производная n-ого порядка (n-я производная) от функции y= f( x) есть производная от ее (n-1)-й производной: 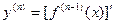 .
.
Рассмотрим примеры.
Пример 1: Найти производную второго порядка 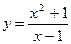 .
.
Решение: 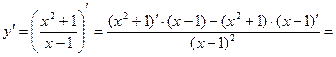
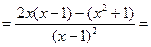
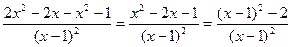
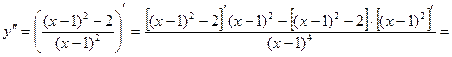
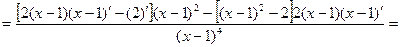
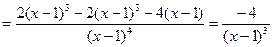
Пример2: Найти производную второго порядка функции 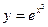 .
.
Решение: 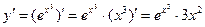
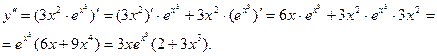
Таблица интегралов
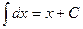
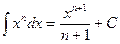
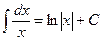
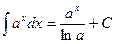
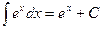
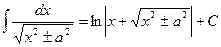
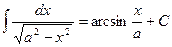
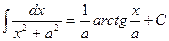 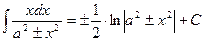
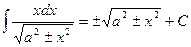
| 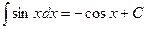
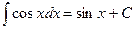
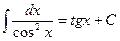
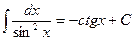
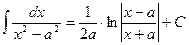
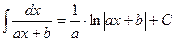
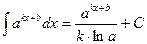
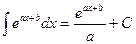 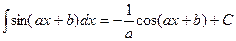 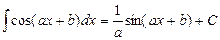
|
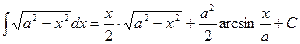
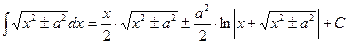
Рассмотрим нахождение интегралов непосредственным методом.
Пример 1: Найти неопределенный интеграл:
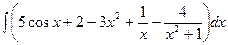 .
.
Решение: 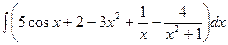 =
=
= 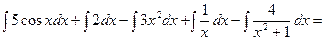
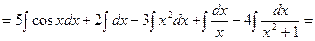

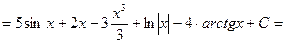
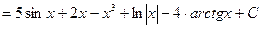 .
.
Пример 2: Найти неопределенный интеграл: 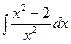 .
.
Решение: 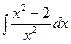 =
= 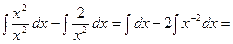

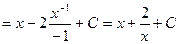 .
.
Пример 3: Найти неопределенный интеграл 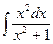
Решение: 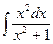 =
= 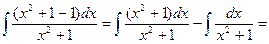
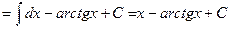
Сумма комплексных чисел.
Определение 4.2. Суммой двух комплексных чисел а + bi и с + di будем называть комплексное число (а + c) + (b + d)i.
Определение 4.3. Произведением двух комплексных чисел а + bi и с + di будем называть комплексное число (ас - bd) + (ad + bc)i.
Пример:
Найти сумму и произведение комплексных чисел z 1=2-5i , z2= -7+i.
z 1 + z 2=(2 – 7) + (-5 + 1)i;
z *z 2=(-14 +5) +(2 + 35)i=-9 + 37i.
Модуль комплексного числа.
Определение 4.4.. Модулем комплексного числа z =а + bi называется число 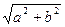 и обозначается
и обозначается 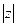 , т.е.
, т.е. 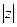 =
= 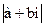 =
= 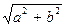 .
.
Пример:
Найти модуль комплексных чисел: а) 2-5i, б) -7+i.
Решение а) 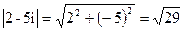 ;
;
б) 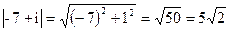 .
.
Формулы Муавра
Возведение в целую степень п. Модуль возводится в эту степень, аргумент умножается на п.
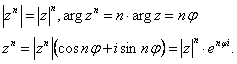 (1)
(1)
Извлечение корня степени п. Извлекается арифметический корень из модуля, общее значение аргумента делится на п. Корень имеет ровно п различных значений, если 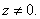
 (2)
(2)
Формулы (1) и (2 называются формулами Муавра
Вопросы для самопроверки по теме 4 Основы теории комплексных чисел
1. Что называется комплексным числом?
2. Какие интерпретации комплексных чисел вы знаете? Опишите их.
3. Что называется действительной и мнимой частями комплексного числа?
4. Что называется алгебраической и тригонометрической формами комплексного числа?
5. В каком случае два комплексных числа называются сопряженными?
6. По каким правилам производятся арифметические действия над комплексными числами?
7. Запишите формулу Муавра.
Варианты контрольных заданий
Задание 1: Дана система линейных уравнений, доказать ее совместность и решить тремя способами:
1) Методом Гаусса;
2) По формулам Крамера;
3) Средствами матричного исчисления.
Вариант 1 . 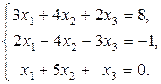 Вариант 2.
Вариант 2. 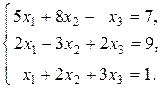
Вариант 3.  Вариант 4.
Вариант 4. 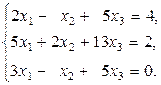
Вариант 5. 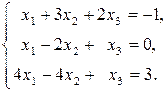 Вариант 6.
Вариант 6. 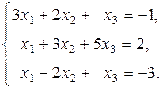
Вариант 7. 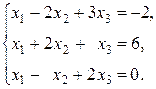 Вариант 8.
Вариант 8. 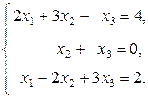
Вариант 9. 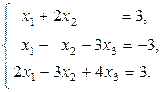 Вариант 10.
Вариант 10. 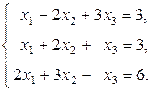
Вариант 11. 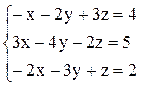 Вариант 12.
Вариант 12. 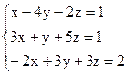
Вариант 13.  Вариант 14.
Вариант 14. 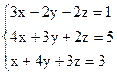
Вариант 15. 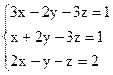 Вариант 16.
Вариант 16. 
Вариант 17. 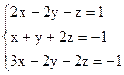 Вариант 18.
Вариант 18. 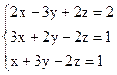
Вариант 19. 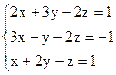 Вариант 20.
Вариант 20. 
Вариант 21. 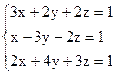 Вариант 22.
Вариант 22. 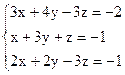
Вариант 23. 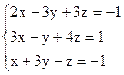 Вариант 24.
Вариант 24. 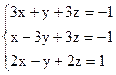
Вариант 25. 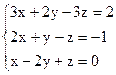 Вариант 26.
Вариант 26. 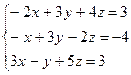
Вариант 27.  Вариант 28.
Вариант 28. 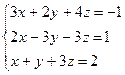
Вариант 29.  Вариант 30.
Вариант 30. 
Задание 2: Вычислить пределы функций
Вариант 1:
а) 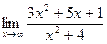 б)
б) 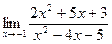 в)
в) 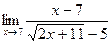 г)
г) 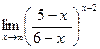
Вариант 2:
а)  б)
б)  в)
в)  г)
г) 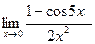
Вариант 3:
а) 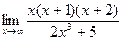 б)
б) 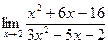 в)
в) 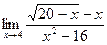 г)
г) 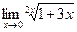
Вариант 4:
а) 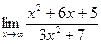 б)
б)  в)
в) 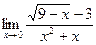 г)
г) 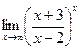
Вариант 5:
а) 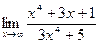 б)
б)  в)
в) 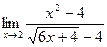 г)
г) 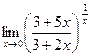
Вариант 6:
а) 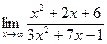 б)
б) 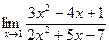 в)
в)  г)
г) 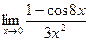
Вариант 7:
а)  б)
б)  в)
в) 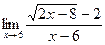 г)
г) 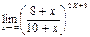
Вариант 8:
а) 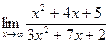 б)
б) 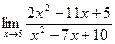 в)
в) 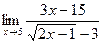 г)
г) 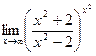
Вариант 9:
а) 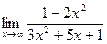 б)
б) 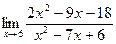 в)
в) 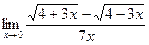 г)
г) 
Вариант 10:
а) 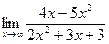 б)
б) 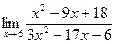 в)
в) 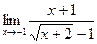 г)
г) 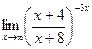
Вариант 11:
а) 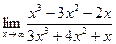 б)
б) 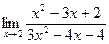 в)
в) 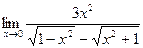 г)
г) 
Вариант 12:
а) 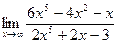 б)
б) 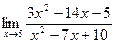 в)
в) 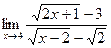 г)
г) 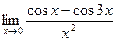
Вариант 13:
а) 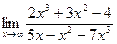 б)
б) 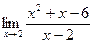 в)
в) 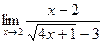 г)
г) 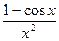
Вариант 14:
а) 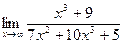 б)
б) 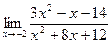 в)
в) 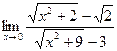 г)
г) 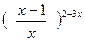
Вариант 15:
а) 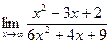 б)
б) 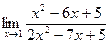 в)
в) 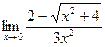 г)
г) 
Вариант 16:
а) 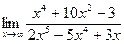 б)
б) 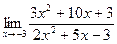 в)
в) 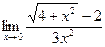 г)
г) 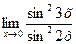
Вариант 17:
а)  б)
б) 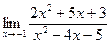 в)
в) 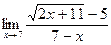 г)
г) 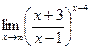
Вариант 18:
а) 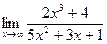 б)
б) 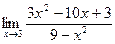 в)
в) 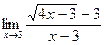 г)
г) 
Вариант 19:
а) 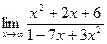 б)
б)  в)
в) 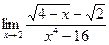 г)
г) 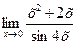
Вариант 20:
а)  б)
б) 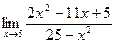 в)
в) 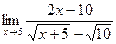 г)
г) 
Вариант 21:
а) 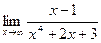 б)
б) 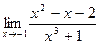 в)
в) 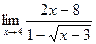 г)
г) 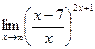
Вариант 22:
а) 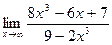 б)
б)  в)
в) 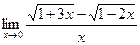 г)
г) 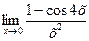
Вариант 23:
а) 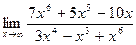 б)
б) 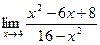 в)
в) 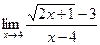 г)
г) 
Вариант 24:
а) 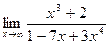 б)
б)  в)
в) 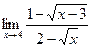 г)
г) 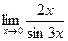
Вариант 25:
а) 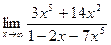 б)
б) 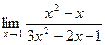 в)
в) 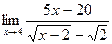 г)
г) 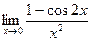
Вариант 26:
а) 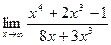 б)
б) 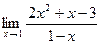 в)
в) 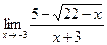 г)
г) 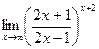
Вариант 27:
а) 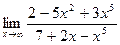 б)
б) 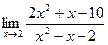 в)
в) 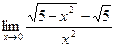 г)
г) 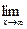
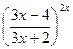
Вариант 28:
а) 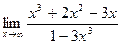 б)
б) 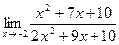 в)
в) 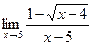 г)
г) 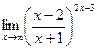
Вариант 29:
а) 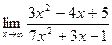 б)
б)  в)
в)  г)
г) 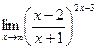
Вариант 30:
а) 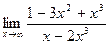 б)
б) 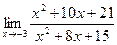 в)
в) 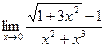 г)
г) 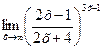
Задание 3 . Найти производные функций.
В пункте в) найти вторую производную:
Вариант 1:
а) 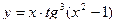 б)
б) 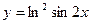 в)
в) 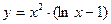
Вариант 2:
а) 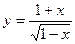 б)
б) 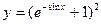 в)
в) 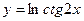
Вариант 3:
а) 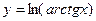 б)
б) 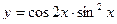 в)
в) 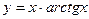
Вариант 4:
а) 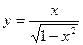 б)
б) 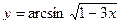 в)
в) 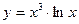
Вариант 5:
а) 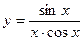 б)
б)  в)
в) 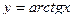
Вариант 6:
а) 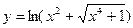 б)
б)  в)
в) 
Вариант 7:
а) 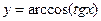 б)
б) 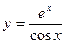 в)
в) 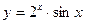
Вариант 8:
а) 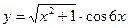 б)
б)  в)
в) 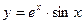
Вариант 9:
а) 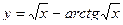 б)
б) 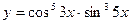 в)
в) 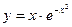
Вариант 10:
а) 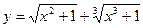 б)
б)  в)
в) 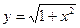
Вариант 11:
а) 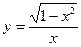 б)
б) 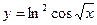 в)
в) 
Вариант 12:
а) 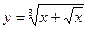 б)
б)  в)
в) 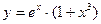
Вариант 13:
а) 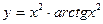 б)
б) 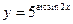 в)
в) 
Вариант 14:
а) 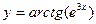 б)
б) 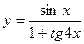 в)
в) 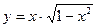
Вариант 15:
а) 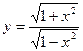 б)
б) 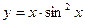 в)
в) 
Вариант 16:
а) 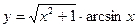 б)
б) 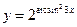 в)
в) 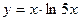
Вариант 17:
а) 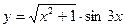 б)
б) 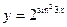 в)
в) 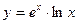
Вариант 18:
а)  б)
б) 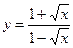 в)
в) 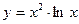
Вариант 19:
а) 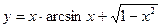 б)
б)  в)
в) 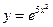
Вариант 20:
а) 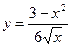 б)
б) 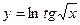 в)
в) 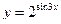
Вариант 21:
а) 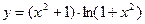 б)
б)  в)
в) 
Вариант 22:
а) 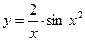 б)
б) 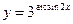 в)
в) 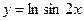
Вариант 23:
а) 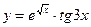 б)
б) 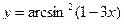 в)
в) 
Вариант 24:
а) 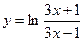 б)
б) 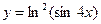 в)
в) 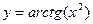
Вариант 25:
а) 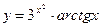 б)
б)  в)
в) 
Вариант 26:
а) 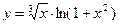 б)
б) 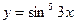 в)
в) 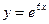
Вариант 27:
а)  б)
б) 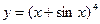 в)
в) 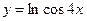
Вариант 28:
а) 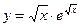 б)
б)  в)
в) 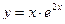
Вариант 29:
а) 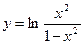 б)
б) 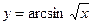 в)
в) 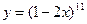
Вариант 30:
а) 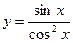 б)
б) 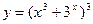 в)
в) 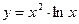
Задание 4: Исследовать функцию и построить график
Вариант 1. 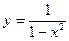
| Вариант 2. у= 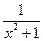
|
Вариант 3. 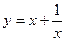
| Вариант 4. 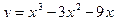
|
Вариант 5. 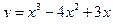
| Вариант 6. 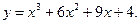
|
Вариант 7. 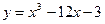
| Вариант 8. 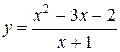
|
Вариант 9. 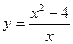
| Вариант 10. 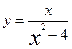
|
Вариант 11. 
| Вариант 12. 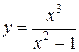
|
Вариант 13. 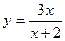
| Вариант 14. 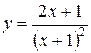
|
Вариант 15. 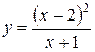
| Вариант 16. 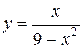
|
Вариант 17. 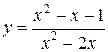
| Вариант 18. 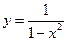
|
Вариант 19. 
| Вариант 20. 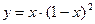
|
Вариант 21. 
| Вариант 22. 
|
Вариант 23. 
| Вариант 24. 
|
Вариант 25. 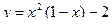
| Вариант 26. 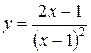
|
Вариант 27. 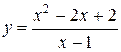
| Вариант 28. 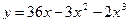
|
Вариант 29. 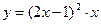
| Вариант 30. 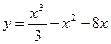
|
Задание 5: Найти неопределенные интегралы и вычислить определенный интеграл:
Вариант 1:
а) 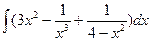 б)
б) 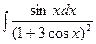 в)
в) 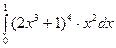
Вариант 2:
а) 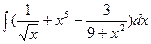 б)
б) 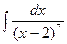 в)
в) 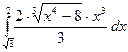
Вариант 3:
а) 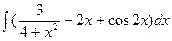 б)
б) 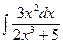 в)
в) 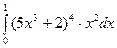
Вариант 4:
а) 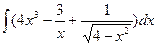 б)
б)  в)
в) 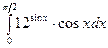
Вариант 5:
а) 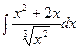 б)
б) 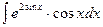 в)
в) 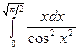
Вариант 6:
а)  б)
б) 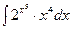 в)
в) 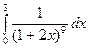
Вариант 7:
а) 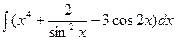 б)
б) 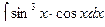 в)
в) 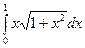
Вариант 8:
а) 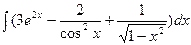 б)
б) 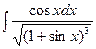 в)
в) 
Вариант 9:
а) 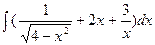 б)
б) 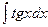 в)
в) 
Вариант 10:
а) 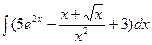 б)
б) 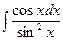 в)
в) 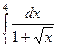
Вариант 11:
а) 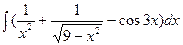 б)
б)  в)
в) 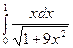
Вариант 12:
а) 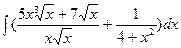 б)
б) 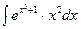 в)
в) 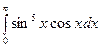
Вариант 13:
а) 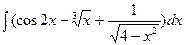 б)
б) 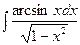 в)
в) 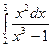
Вариант 14:
а) 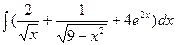 б)
б) 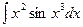 в)
в) 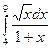
Вариант 15:
а) 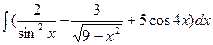 б)
б) 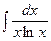 в)
в) 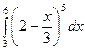
Вариант 16:
а) 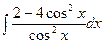 б)
б) 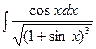 в)
в) 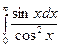
Вариант 17:
а) 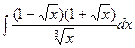 б)
б) 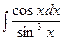 в)
в) 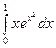
Вариант 18:
а) 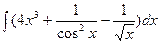 б)
б) 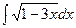 в)
в) 
Вариант 19:
а) 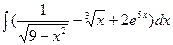 б)
б) 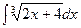 в)
в) 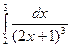
Вариант 20:
а) 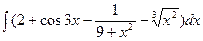 б)
б) 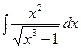 в)
в) 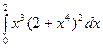
Вариант 21:
а) 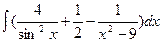 б)
б)  в)
в) 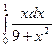
Вариант 22:
а) 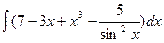 б)
б) 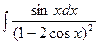 в)
в) 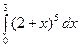
Вариант 23:
а) 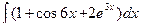 б)
б) 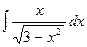 в)
в) 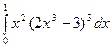
Вариант 24:
а) 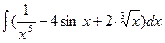 б)
б) 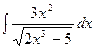 в)
в) 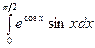
Вариант 25:
а) 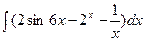 б)
б) 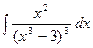 в)
в) 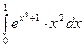
Вариант 26:
а) 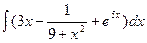 б)
б) 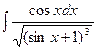 в)
в) 
Вариант 27:
а) 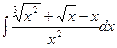 б)
б) 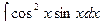 в)
в) 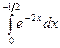
Вариант 28:
а) 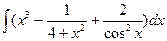 б)
б) 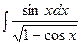 в)
в) 
Вариант 29:
а) 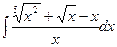 б)
б) 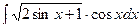 в)
в) 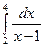
Вариант 30:
а) 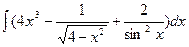 б)
б)  в)
в) 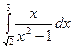
Задание 6: Вычислить площадь фигуры, ограниченной указанными линиями. Сделать чертёж.
Вариант 1. 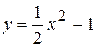 ; ; 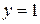
| Вариант 2. 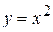 ; ; 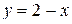
|
Вариант 3. 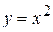 ; ; 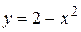
| Вариант 4.  ; ; 
|
Вариант 5. 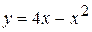 ; ; 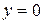
| Вариант 6. 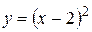 ; ; 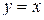
|
Вариант 7. 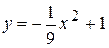 ; ; 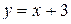
| Вариант 8. 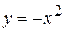 ; ; 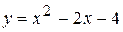
|
Вариант 9. 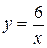 ; ; 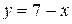
| Вариант 10. 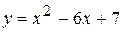 ; ; 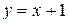
|
Вариант 11. 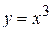 ; ; 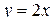
| Вариант 12. 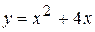 ; ; 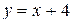
|
Вариант 13.  ; ; 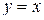
| Вариант 14.  ; ; 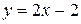
|
Вариант 15. 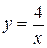 ; ; 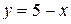
| Вариант 16. 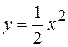 ; ; 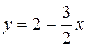
|
Вариант 17.  ; ; 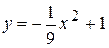 ; ; 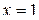
| Вариант 18. 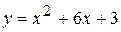 ; ; 
|
Вариант 19. 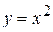 ; ; 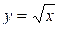
| Вариант 20. 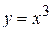 ; ; 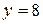 ; ; 
|
| Вариант 21. у=х2-8х+16, у=6-х | Вариант 22. у=-х2+8х-11, у=х-1 |
| Вариант 23. у=-х2+6х-7, у=х2-6х+9 | Вариант 24. у=-х2+4х-2, у=х2-4х+4 |
| Вариант 25. у=х2-8х+17, у=-х2+10х-19 | Вариант 26. 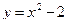 , , 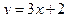
|
| Вариант 27. у = -х2+2х+9, у = 3х2-6х+5 | Вариант 28. у=2х2+4х-5, у=х-4 |
| Вариант 29. у=(х-2)3, у=4х-8 | Вариант 30. у=х2-4х+7, у=3 |
Задание 7: Дано комплексное число  . Требуется: 1) записать его в алгебраической и тригонометрической формах; 2) найти все корни уравнения
. Требуется: 1) записать его в алгебраической и тригонометрической формах; 2) найти все корни уравнения 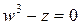 .
.
Вариант 1. 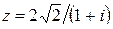
| Вариант 2. 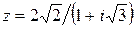
|
Вариант 3. 
| Вариант 4. 
|
Вариант 5. 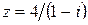
| Вариант 6. 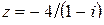
|
Вариант 7. 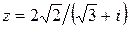
| Вариант 8. 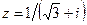
|
Вариант 9. 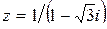
| Вариант 10. 
|
Вариант 11. 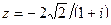
| Вариант 12. 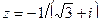
|
Вариант 13. 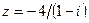
| Вариант 14. 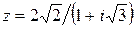
|
Вариант 15. 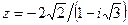
| Вариант 16. 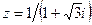
|
Вариант 17. 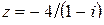
| Вариант 18. 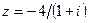
|
Вариант 19. 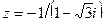
| Вариант 20. 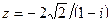
|
Вариант 21. 
| Вариант 22. 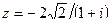
|
Вариант 23. 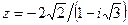
| Вариант 24. 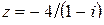
|
Вариант 25. 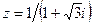
| Вариант 26. 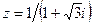
|
Вариант 27. 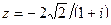
| Вариант 28. 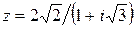
|
Вариант 29. 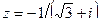
| Вариант 30. 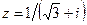
|
Решение типового варианта
Задание 1: Дана система линейных уравнений:
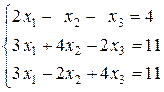
доказать ее совместность и решить тремя способами:
1) Методом Гаусса;
2) По формулам Крамера;
3) Средствами матричного исчисления.
Решение: Теорема Кронекера-Капелли. Система совместна тогда и только тогда, когда ранг матрицы этой системы равен рангу ее расширенной матрицы, т. е. r(A)= r(A1), где
 ,
, 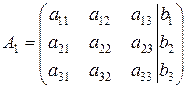 .
.
Расширенная матрица системы имеет вид:
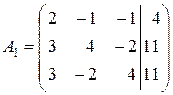 .
.
Умножим первую строку на (–3),а вторую на (2); прибавим после этого элементы первой строки к соответствующим элементам второй строки; вычтем из второй строки третью. В полученной матрице первую строку оставляем без изменений.
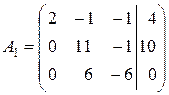 ~
~
Разделим элементы третьей строки на (6) и поменяем местами вторую и третью строки:
~  ~
~
Умножим вторую строку на (–11) и прибавим к соответствующим элементам третьей строки.
~ 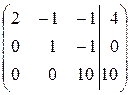
Разделим элементы третьей строки на (10).
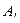 ~
~ 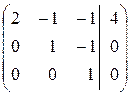 ;
;  ~
~ 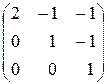 .
.
Найдем определитель матрицы А.
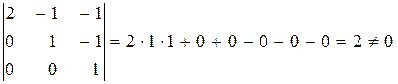 .
.
Следовательно, r(A)=3. Ранг расширенной матрицы r(A1) так же равен 3, т.е.
r(A)= r(A1)=3 Þ система совместна.
1) Исследуя систему на совместность, расширенную матрицу преобразовали по методу Гаусса.
Метод Гаусса состоит в следующем:
1. Приведение матрицы к треугольному виду, т. е. ниже главной диагонали должны находиться нули (прямой ход).
2. Из последнего уравнения находим х3 и подставляем его во второе, находим х2, и зная х3, х2 подставляем их в первое уравнение, находим х1 (обратный ход).
Запишем, преобразованную по методу Гаусса, расширенную матрицу
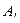 ~
~ 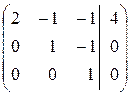
в виде системы трех уравнений:
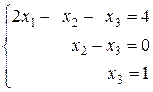 Þ х3=1
Þ х3=1
х2=х3 Þ х3=1
2х1=4+х2+х3 Þ 2х1=4+1+1 Þ
Þ 2х1=6 Þ х1=3
Ответ: х1=3 , х2=1, х3=1.
2) Решим систему по формулам Крамера: если определитель системы уравнений Δ отличен от нуля, то система имеет единственное решение, которое находится по формулам
 ;
; 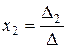 ;
; 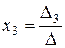 .
.
Вычислим определитель системы Δ:
 Т.к. определитель системы отличен от нуля, то согласно правилу Крамера, система имеет единственное решение. Вычислим определители Δ1, Δ2, Δ3. Они получаются из определителя системы Δ заменой соответствующего столбца на столбец свободных коэффициентов.
Т.к. определитель системы отличен от нуля, то согласно правилу Крамера, система имеет единственное решение. Вычислим определители Δ1, Δ2, Δ3. Они получаются из определителя системы Δ заменой соответствующего столбца на столбец свободных коэффициентов.

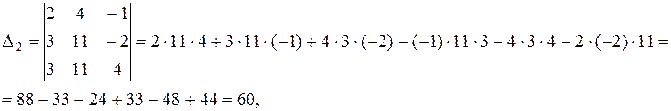
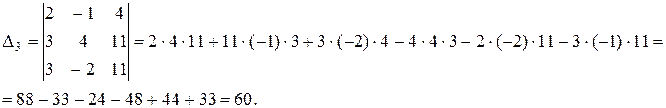 Находим по формулам неизвестные:
Находим по формулам неизвестные:
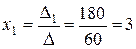 ;
; 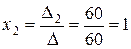 ;
; 
Ответ: х1=3 , х2=1, х3=1.
3) Решим систему средствами матричного исчисления, т. е. при помощи обратной матрицы.
А ×Х=В Þ Х=А-1 × В, где А-1 – обратная матрица к А,
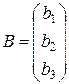 - столбец свободных членов,
- столбец свободных членов,
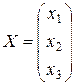 - матрица-столбец неизвестных.
- матрица-столбец неизвестных.
Обратная матрица считается по формуле:
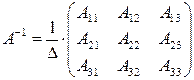 (*)
(*)
где D - определитель матрицы А, А ij – алгебраические дополнения элемента аij матрицы А. D = 60 (из предыдущего пункта). Определитель отличен от нуля, следовательно, матрица А обратима, и обратную к ней матрицу можно найти по формуле (*). Найдем алгебраические дополнения для всех элементов матрицы А по формуле:
А ij =(-1)i+j Mij .
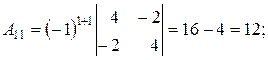

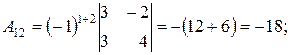
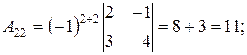
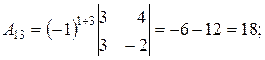
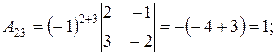
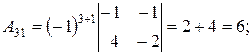
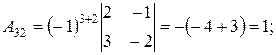
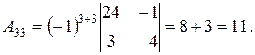
Запишем обратную матрицу.
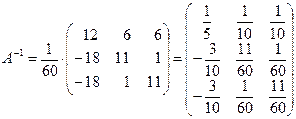 .
.
Сделаем проверку по формуле: А-1 × А=Е.
А-1А=
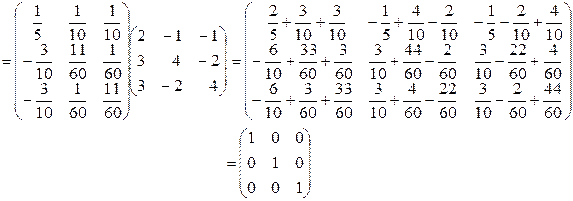
Вывод: так как произведение А-1 × А дает единичную матрицу, то обратная матрица А-1 найдена верно и решение системы определяется по формуле Х=А-1 ×В.
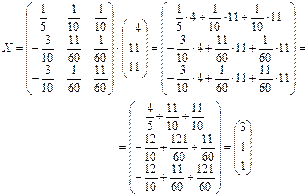 .
.
Ответ: х1=3 , х2=1, х3=1.
Проверка. Подставим полученные значения в систему. Получим:
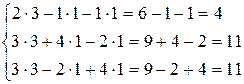
Т. к. неизвестные х1 , х2, х3 обратили каждое уравнение в тождество, то они найдены верно.
Задание 2: Вычислить пределы, не пользуясь правилом Лопиталя
а) 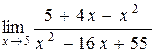 ;
;
Функция  не определена при х=5 и поэтому разрывна в этой точке. Числитель и знаменатель в точке х=5 обращается в нуль, налицо неопределенность
не определена при х=5 и поэтому разрывна в этой точке. Числитель и знаменатель в точке х=5 обращается в нуль, налицо неопределенность 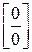 . Выделим общий множитель (х-5) и сократим на него числитель и знаменатель, считая х¹5, х ® 5.
. Выделим общий множитель (х-5) и сократим на него числитель и знаменатель, считая х¹5, х ® 5.
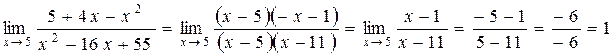 .
.
б) 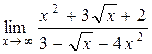 ;
;
Ни числитель, ни знаменатель этой дроби не имеют конечного предела так как они неограниченно возрастают при неограниченном возрастании х, т. е. имеем дело с неопределенностью 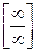 . Поделим числитель и знаменатель дроби на х2:
. Поделим числитель и знаменатель дроби на х2:

так как 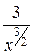 ,
,  ,
, 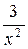 ,
, 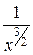 при х ® ¥ – величины бесконечно малые.
при х ® ¥ – величины бесконечно малые.
в) 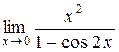 ;
;
Поскольку числитель и знаменатель обращаются в нуль при х=0, то имеем дело с неопределенностью вида 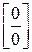 .
.
Воспользуемся тригонометрической формулой для преобразования знаменателя 2 sin2 x=1- cos2 x и получим предел, в котором участвует тригонометрическая функция sinx.
Применив первый замечательный предел 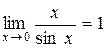 , получаем:
, получаем:
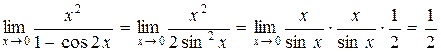 ,
,
так как 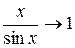 при х ® 0.
при х ® 0.
г) 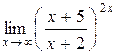 .
.
Предел функции 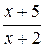 при х ® 0 равен единице, т.е. в данном примере требуется раскрыть неопределенность
при х ® 0 равен единице, т.е. в данном примере требуется раскрыть неопределенность 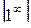 . Примеры такого вида сводятся ко второму замечательному пределу
. Примеры такого вида сводятся ко второму замечательному пределу 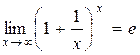 .
.
Преобразуем выражение в скобках к виду 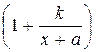
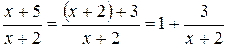 .
.
Тогда
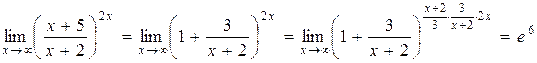 ,
,
т. к. 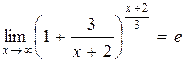 ,
,  .
.
Задание 3: Найти производные следующих функций
а) Найти производную функции 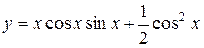 .
.
Решение:
Сначала преобразуем данную функцию: 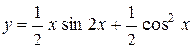
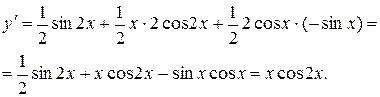
б) Найти производную функции 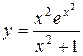 .
.
Решение:
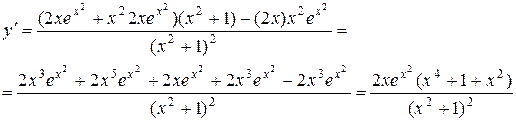
в) Найти производную функции 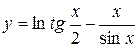 .
.
Решение:
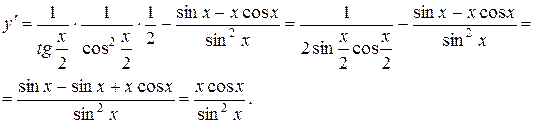
г) Найти производную функции 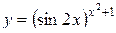 .
.
Решение:
Логарифмируем данную функцию
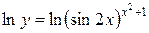 ,
,
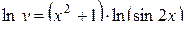 ,
,
Дифференцируем
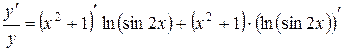 ,
,
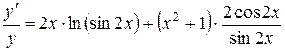 ,
,
Выражаем
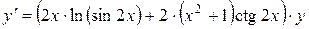 .
.
Или
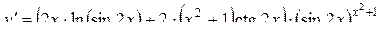 .
.
Задание 4: Исследовать функцию  и построить график.
и построить график.
Решение.
1. Данная функция не определена при 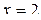 , т. к. в этой точке знаменатель обращается в ноль. Значит
, т. к. в этой точке знаменатель обращается в ноль. Значит
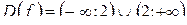 .
.
2. 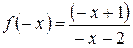

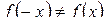 ,
, 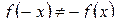 . Следовательно, функция общего вида.
. Следовательно, функция общего вида.
3. Не периодична.
4. Точки пересечения с осью Ох: 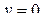 при
при 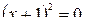 ,
,  . С осью Оу:
. С осью Оу:  ,
,
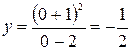 . Нашли две точки пересечения графика функции с осями координат:
. Нашли две точки пересечения графика функции с осями координат: 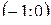 и
и 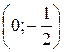 .
.
5. Исследуем на непрерывность. Точкой разрыва является  . Определим тип разрыва. Для этого найдем односторонние пределы функции в данной точке.
. Определим тип разрыва. Для этого найдем односторонние пределы функции в данной точке.
 и
и 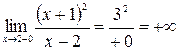 .
.
Значит,  - точка разрыва второго рода.
- точка разрыва второго рода.
6. Из предыдущего пункта следует, что  - вертикальная асимптота.
- вертикальная асимптота.
Найдем наклонную асимптоту 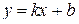 .
.
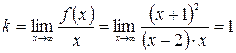 .
. 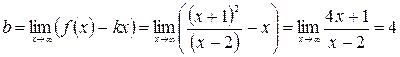 .
.
Итак, 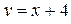 - наклонная асимптота.
- наклонная асимптота.
7. Исследуем на возрастание, убывание и экстремум функции. Для этого найдем производную функции.
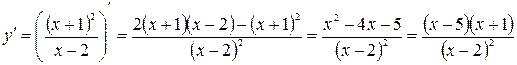 .
.
Найдем точки, в которых производная равна нулю 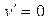 .
.


 и
и  .
.
Далее отметим данные точки на числовой оси и к ним добавляем точку  , в которой
, в которой 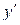 не определена.
не определена.

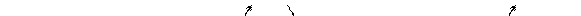
Находим интервалы, на которых 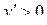 :
: 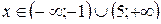 и
и
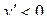 :
:  .
.
При прохождении точки  производная меняет знак с плюса на минус. Следовательно,
производная меняет знак с плюса на минус. Следовательно,  - точка экстремума функции, а именно максимум.
- точка экстремума функции, а именно максимум.
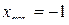
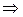
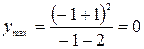 .
.
При прохождении точки  производная меняет знак с минуса на плюс. Следовательно,
производная меняет знак с минуса на плюс. Следовательно,  так же является точкой экстремума функции, а именно минимумом.
так же является точкой экстремума функции, а именно минимумом.
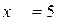
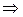
 .
.
8. Исследуем на вогнутость функции и точки перегиба. Для этого находим производную второго порядка.
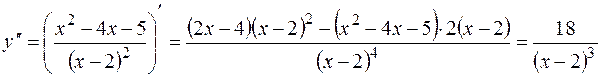 .
.
Вторая производная в ноль никогда не обращается, поэтому на числовой оси отмечаем только  .
.
 :
:  - функция вогнута и
- функция вогнута и 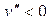 :
: 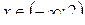 - выпукла. Точек перегиба нет.
- выпукла. Точек перегиба нет.
Составим таблицу, в которую занесем полученные сведения.
| х | 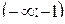
| -1 | 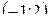
| 2 | 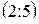
| 5 | 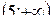
|
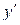
| + | 0 | - | не сущ. | - | 0 | + |
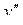
| - | - | не сущ. | + | + | ||
| у |  
| 
|  
| верт. ас. |  
| 
|  
|
После того, как собрали все данные, полученные в ходе исследования, изобразим характерное поведение графика данной функции. (См. рис.).
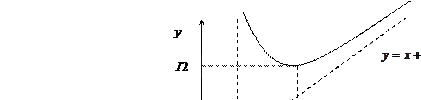
Задание 5: Найти неопределенные интегралы и вычислить определенный интеграл
а)  ;
;
Делая замену 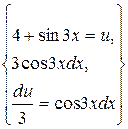 , получаем:
, получаем:
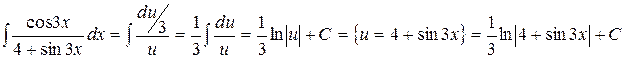 .
.
б) 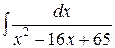 ;
;
Выделяем полный квадрат в знаменателе дроби 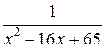 . Получаем х2-16х+65=(х-4)2+42+65=(х-4)2-16+65=(х-4)2+49.
. Получаем х2-16х+65=(х-4)2+42+65=(х-4)2-16+65=(х-4)2+49.
Тогда получаем табличный интеграл типа: 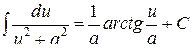 .
.
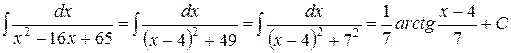 .
.
в) 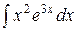 ;
;
Применим два раза формулу интегрирования по частям
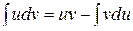 .
.
Получаем
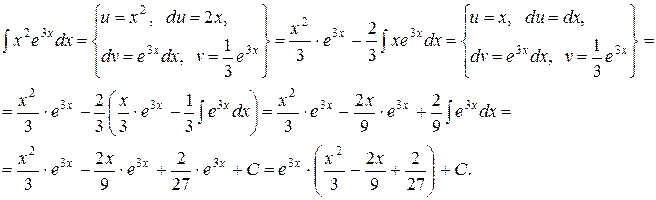
г) 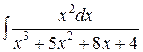 .
.
Разложим знаменатель дроби 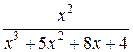 на множители. Получаем:
на множители. Получаем:
х3+5х2+8х+4=(х+1)×(х2+4х+4)=(х+1)×(х+2)2 .
Множителю (х+2)2 соответствует сумма двух простейших дробей 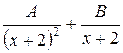 , т. к. кратность корня х=-2 равняется двум. Множителю (х+1) – простейшая дробь
, т. к. кратность корня х=-2 равняется двум. Множителю (х+1) – простейшая дробь 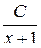 .
.
Итак, подынтегральная функция может быть представлена в виде суммы трех простейших дробей.
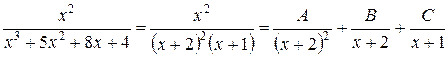 .
.
Приводим к общему знаменателю и, приравнивая числители двух последних дробей, получаем
х2=А (х+1)+В(х+2)(х+1)+С(х+2)2,
х2=Ах+А+Вх2+3Вх+2В+Сх2+4Сх+4С.
Сгруппируем члены при одинаковых степенях х.
х2=х2(В+С)+х(А+3В)+х0(А+2В+4С).
Приравнивая коэффициенты при одинаковых степенях х, получаем

В итоге имеем систему
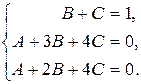
Решая систему одним из известных методов, получаем А=-4, В=0, С=1.
Итак, разложение рациональной дроби на простейшие, имеет вид
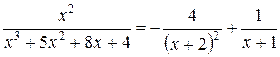 .
.
Таким образом,
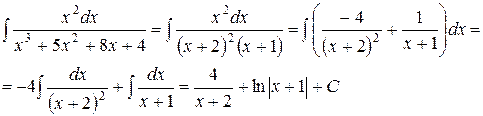 .
.
д) 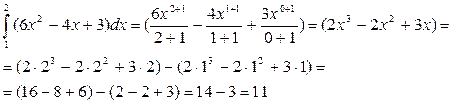
Задание 6: Найти площадь фигуры, ограниченной линиями
y = x, y = x2, x = 2.
Решение:

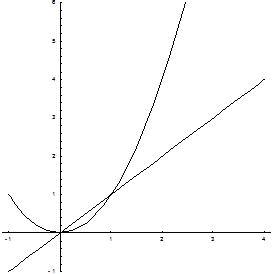
Искомая площадь (заштрихована на рисунке) может быть найдена по формуле:
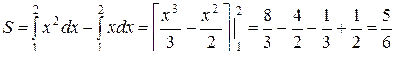 (ед2)
(ед2)
Задание 7:Дано комплексное число z. Требуется:
- записать число z в алгебраической и тригонометрической формах;
- найти все корни уравнения
 .
.
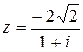 .
.
Решение:
1) Комплексное число z в алгебраической форме имеет вид: z=а+ bi;
в тригонометрической форме: z= r( cos j+ i × sin j), где 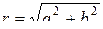 и
и 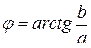 .
.
Для тог чтобы записать 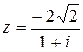 в алгебраической форме, умножим числитель и знаменатель на сопряженное к знаменателю, т. е. на 1- i.
в алгебраической форме, умножим числитель и знаменатель на сопряженное к знаменателю, т. е. на 1- i.
 .
.
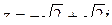 - алгебраическая форма.
- алгебраическая форма.
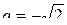 ,
, 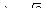 ,
, 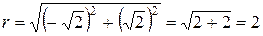 ,
,
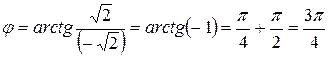 .
.
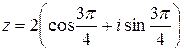 - тригонометрическая форма.
- тригонометрическая форма.
2) 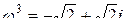 Þ
Þ 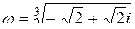 .
.
Так как число 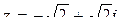 в тригонометрической форме
в тригонометрической форме
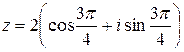 Þ
Þ
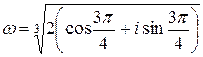 .
.
Применяя формулу для извлечения корня из комплексного числа:
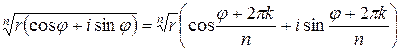 ,
,
получаем 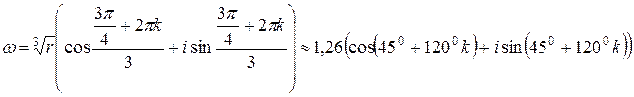
Если k=0, то 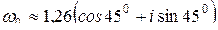 ;
;
Если k=1, то 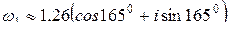 ;
;
Если k=2, то 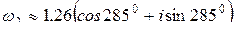 .
.
Следовательно, корни уравнения в алгебраической форме имеет вид
Ответ:
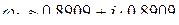 ,
,
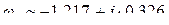 ,
,
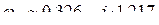 .
.
Учебно – методическое обеспечение дисциплины
Перечень рекомендуемые учебных изданий, интернет – ресурсов, дополнительной литературы:
Основные источники:
1. Учебник для студентов образовательных учреждений среднего профессионального образования «Математика» И.Д.Пехлецкий., Москва: Асаdemia, 2002
2. Письменный Д.В Конспект лекций по высшей математике (I часть)М.Рольф.2002
3. Письменный Д.В Конспект лекций по высшей математике (II часть)М.Рольф.2002
Дополнительные источники:
1. Алексеев А.С., Белоновская Л.Н. и др. Дидактические материалы (для 10 классов вечерней общеобразовательной школы) М.Просвещение. 1988
2. Брадис В.М.4-х значные математические таблицы.М.Просвещение .1974
3. Виленкин Н.Я., Мордкович А.Г.Производная и интеграл. М. Просвещение.1993
4. Выгодский М.Я.Справочник по высшей математике .М. Джангар.2001
5. Ганеев Х.Ж.Учителю математики об элементах краеведения. Екатеринбург.1996
6. Гольдич В.А.Алгебра: решение уравнений и неравенств. Санкт-Петербург. Литера.2005
7. Денищева Л.О., Корешкова Т.А. Тематические тесты и зачёты. Алгебра и начала анализа.М. Мнемозина. 2007
8. Денищева Л.О., Кузнецова Л.В. и др. Зачёты в системе дифференцированного обучения.М. Просвещение. 1993 Вариант IМ. Интеллект-центр.2001
9. Звавич Л.И., Поташник А.М. и др.Сборник задач по алгебре и математическому анализу (для 10-11 кл)М.Новая школа.1996
10. Колягин Ю.М., Ткачева М.В, Федерова Н.Е. и др. под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни). 10 кл. – М., 2005.
11. Клеймёнов А.Ф, Шнейдер А.Е. Задачи письменного экзамена по математике за курс старшей и основной школы. ИРРО.1999
12. Колмогорова А.Н. Учебное пособие: Алгебра и начала анализа. М. Просвещение .1982
13. Кочетков Е.С., Кочеткова Е.С. Алгебра и элементарные функции. Часть I М.Просвещение. 1971
14. Кочетков Е.С., Кочеткова Е.С. Алгебра и элементарные функции. Часть II М.Просвещение. 1971
15. Мордкович А.Г., Сухорский А.М.Справочник школьника по математике.10 –11 класс.М.Аквариум. 1989
16. Никольский С.М., Потапов М.К., Решетников Н.Н. и др. Алгебра и начала математического анализа (базовый и профильный уровни). 11 кл. – М., 2006.
17. Никольский С.М., Потапов М.К., Решетников Н.Н. и др. Алгебра и начала математического анализа (базовый и профильный уровни). 10 кл. – М., 2006.
18. Саакян С.М., Гольдман А.М. и др.Задачи по алгебре и началам анализа ,10- 11 класс.М.Просвещение. 1992
19. Черкасов Р.С., Столяр А.А.Методика преподавания математики.М. Просвещение. 1985
20. Фирсов В.В.Планирование обязательных результатов обучения математике.М.Просвещение. 1989
21. Шарыгин И.Ф., голубеев В.И.Факультативный курс по математике (решение задач).М .Просвещение.1991
Интернет-ресурсы:
http://www.youtube.com/watch?v=TxFmRLiSpKo (Геометрический смысл производной)
http://www.youtube.com/watch?v=PbbyP8oEv-g (Лекция 1. Первообразная и неопределенный интеграл)
http://www.youtube.com/watch?v=2N-1jQ_T798&feature=channel (Лекция 5. Интегрирование по частям)
http://www.youtube.com/watch?v=3qGZQW36M8k&feature=channel (Лекция 4. Таблица основных интегралов)
http://www.youtube.com/watch?v=7lezxG4ATcA&feature=channel (Лекция 3. Непосредственное интегрирование)
http://www.youtube.com/watch?v=s-FDv3K1KHU&feature=channel (Лекция 4. Метод подстановки)
http://www.youtube.com/watch?v=dU_FMq_lss0&feature=channel (Лекция 12.Понятие определенного интеграла)
http://www.youtube.com/watch?v=wg_AIYBB0dg&feature=related (Гиперметод умножения)
http://www.youtube.com/watch?v=C_7clQcJP-c (Теория вероятности)
http://www.youtube.com/watch?v=dZPRzB1Nj08 (Лекция 6. Комплексные числа (часть 1))
http://www.youtube.com/watch?v=Cfy0CXpR9Lo (Комплексные числа и фракталы. Часть 1)
http://www.youtube.com/watch?v=uis7Hg2gSNo&feature=related (Теория фракталов)
Раздел I Линейная алгебра
Тема 1. Матрицы и определители
Определение 1.1. Матрицей называется прямоугольная таблица чисел.
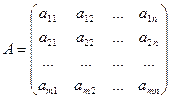
Обозначения: А – матрица, 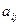 - элемент матрицы,
- элемент матрицы, 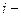 номер строки, в которой стоит данный элемент,
номер строки, в которой стоит данный элемент, 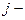 номер соответствующего столбца; m – число строк матрицы, n – число ее столбцов.
номер соответствующего столбца; m – число строк матрицы, n – число ее столбцов.
Определение 1.2. Числа m и n называются размерностями матрицы.
Определение 1.3. Матрица называется квадратной, если m = n. Число n в этом случае называют порядком квадратной матрицы.
Каждой квадратной матрице можно поставить в соответствие число, определяемое единственным образом с использованием всех элементов матрицы. Это число называется определителем.
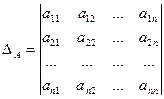
Определение 1.4. Определителем второго порядка называется число, полученное с помощью элементов квадратной матрицы 2-го порядка следующим образом:
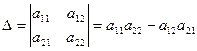 .
.
При этом из произведения элементов, стоящих на так называемой главной диагонали матрицы (идущей из левого верхнего в правый нижний угол) вычитается произведение элементов, находящихся на второй, или побочной, диагонали.
Примеры:
1. 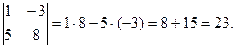 2.
2. 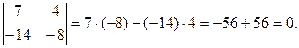
Определение 1.5. Определителем третьего порядка называется число, определяемое с помощью элементов квадратной матрицы 3-го порядка следующим образом:
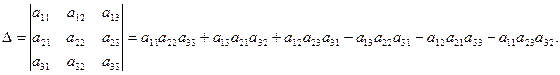
Замечание. Для того, чтобы легче запомнить эту формулу, можно использовать так называемое правило треугольников. Оно заключается в следующем: элементы, произведения которых входят в определитель со знаком «+», располагаются так:















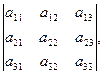 образуя два треугольника, симметричных относительно главной диагонали. Элементы, произведения которых входят в определитель со знаком «-», располагаются аналогичным образом относительно побочной диагонали:
образуя два треугольника, симметричных относительно главной диагонали. Элементы, произведения которых входят в определитель со знаком «-», располагаются аналогичным образом относительно побочной диагонали: 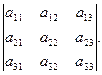
 Примеры.
Примеры.
1. 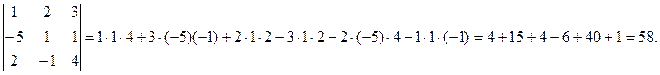
2. 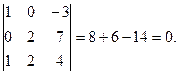
Определение1. 6. Транспонированием матрицы называется операция, в результате которой меняются местами строки и столбцы с сохранением порядка их следования. В результате получается матрица А`, называемая транспонированной по отношению к матрице А, элементы которой связаны с элементами А соотношением a` ij = aji .
Дата: 2018-11-18, просмотров: 419.