Вероятностью события А называется отношение числа исходов (m), благоприятствующих наступлению данного события А, к числу (n) всех исходов (несовместных, единственно возможных и равновозможных). Обозначается: 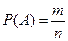 (1)

Свойства вероятности случайного события:

1.  

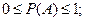
2. 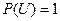, где U- достоверное событие;

3. 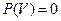 где V- невозможное событие;

4.

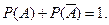
При расчётах вероятностей, т.е. при подсчёте числа событий m и n используют комбинаторику (раздел математики, в котором производится подсчёт возможных различных соединений, составленных из конечного числа элементов по некоторому правилу).

Различают три типа соединений:

1. размещения (2) 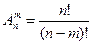           , где 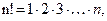 причём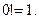

Размещениями из n элементов по m в каждом называются такие соединения, из которых каждое содержит m элементов, взятых из числа данных n элементов, и которые отличаются друг от друга либо самим элементам (хотя бы одним), либо лишь порядком их расположения.

Пример. Из 10 членов собрания нужно выбрать председателя и секретаря. Сколько существует таких соединений?

Так как группа по 2 человека могут отличаться и составом претендентов, и заполняемыми ими вакансиями, то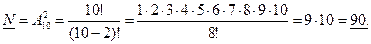

2. перестановки (3)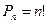

Перестановками из n элементов называются такие соединения из всех n элементов, которые отличаются друг от друга порядком расположения элементов.

Пример. Сколькими способами можно рассадить 7 человек по семи местам?

Т. к. группы по 7 человек отличаются друг от друга порядком расположения, то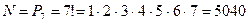

3) Сочетания (4)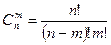

Сочетаниями из n элементов по m в каждом называются такие соединения, которые отличаются друг от друга хотя бы одним элементом.

Пример. Сколькими способами из 15-ти рабочих можно создать бригады по 5 человек в каждом?

Т. к. группы по 5 человек отличаются друг от друга по крайней мере одним человеком, то

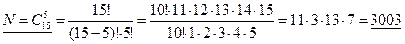
Основой математической статистики служит теория вероятностей, в которой изучаются математические модели реальных случайных явлений. Методы математической статистики дают возможность на основе экспериментальных данных определять вероятностные характеристики этих моделей: математические ожидания, дисперсии, законы распределения и многие другие характеристики.

Опр: Совокупность всех исследуемых объектов называют генеральной совокуностью.

Опр: Выборочной совокупностью или просто выборкой называют совокупность случайно отобранных объектов из генеральной совокупности.

Опр: Число объектов выборочной или генеральной совокупности называют объёмом выборки.

Опр: Выборку, представляющую собой неубывающую последовательность чисел, называют вариационным рядом.

Опр: Разность между наибольшим значением числовой выборки и её наименьшим значением называют размахом выборки.

Опр: Таблица вида   (*)

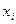
	х1	х2	…		…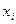
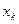
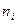
	n1	n2	…		…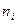
			…		…

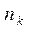
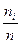
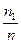
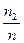
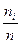
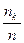
называется статистическим рядом (задаёт выборочное распределение),

где 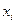 - значение случайной величины;

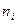 - частота значения ;

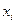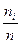 - относительная частота значения ;

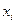n – объём выборки, причём .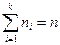

Графическими изображениями выборки являются полигон и гистограмма.

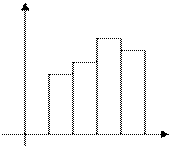
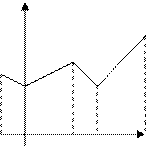
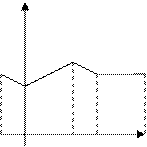Полигон частот.                Полигон относительных частот.           Гистограмма. 

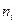
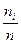
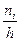
1

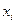
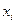                                                                                                   h h h h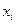

-1 0    3 4     7           0                                                           0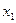

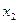
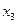
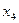
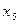
                                                                                                          S_{гистограммы}=1.

Выборочным математическим ожиданием или выборочным средним называют среднее арифметическое значений выборки .

Обозначают 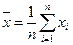; (1)

Если выборка задана рядом (*), то ;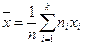

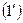
Выборочной дисперсией называют среднее арифметическое квадратов отклонений значений выборки от выборочного среднего.

Обозначают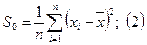

Если выборка задана рядом (*), то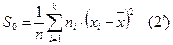

Несмещённая выборочная дисперсия

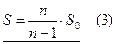 или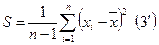

Практическая часть.

Задача 1.

В партии из 10-ти деталей 7 стандартных. Найти вероятность того, что среди 6-ти взятых наудачу деталей 4 стандартных.

Решение. Общее число возможных элементарных исходов испытания равно числу способов, которыми можно извлечь 6 деталей из 10: .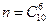

Определим число исходов, благоприятствующих интересующему нас событию А(среди 6 взятых деталей 4 стандартных). 4 стандартные детали можно выбрать из 7 стандартных 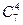 способами, при этом остальные 2=6-4 детали должны быть нестандартными и их выбор можно осуществить  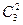способами. Следовательно, число благоприятствующих исходов равно .

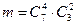Искомая вероятность .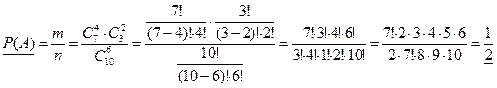

Задача 2

Для выборки x: 4; 5; 3; 2; 1; 2; 0; 7; 7; 8

а) построить: 1) полигон частот;

                    2) полигон относительных частот;

                    3) гистограмму частот

найти: б) выборочное среднее ;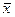

         в) выборочную дисперсию S₀;

         г) несмещенную выборочную дисперсию S.

Решение.

а) Построим статистический ряд (для чего необходимо подсчитать количество (частоты n_i) одинаковых значений x_i):

xi	0	1	2	3	4	5	7	8
ni	1	1	2	1	1	1	2	1

             ;

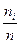
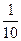
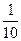
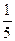
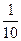
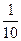
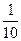
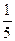
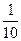
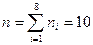
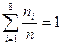Полигон частот.                Полигон относительных частот.           Гистограмма. 

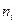
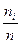
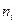
2                                                                                                              2

                                     0,2

1                                          0,1                                                          1

          1 2 3 4 5 6 7 8                      1 2 3 4 5 6 7 8                                       1 2 3 4 5 6 7 8

б) найдем выборочное среднее :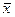

согласно формуле ( )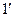

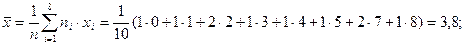
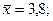
в) найдем выборочную дисперсию S:

согласно формуле ( )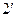

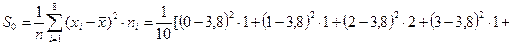
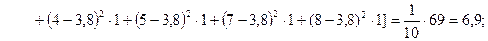
г) найдем несмещенную выборочную дисперсию согласно формуле (3)

     S= 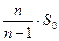= =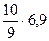7,67