ТЕХНОЛОГИЧЕСКИЙ ИНСТИТУТ (ФИЛИАЛ) ДГТУ в г. Азове
Факультет среднего профессионального образования
Краткий конспект лекций
По дисциплине Математика
По специальности 15.02.08 Технология машиностроения
Составитель
Преподаватель первой категории
Н.М. Булда
Азов
2018
Теоретическая часть.
Тема: Определители. Решение систем линейных уравнений методом Крамера.
Цель: Научиться выполнять различные операции над матрицами и вычислять определители, решать СЛАУ методом Крамера.
О: Матрицей размерности m × n называется прямоугольная таблица действительных чисел, состоящая из m строк и n столбцов.
Числа, составляющие матрицу, называются элементами матрицы. Матрицы обозначаются большими латинскими буквами А, В, С и т. д.
В общем случае матрица имеет вид
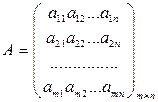
Обозначения: а ij, i– номер строки, j- номер столбца. Множество всех матриц порядка  обозначают
обозначают 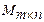 .
.
Виды матриц.
О1: Если число строк в матрице равно числу столбцов, то матрица называется квадратной.
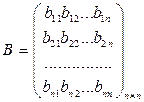
число n называется порядком.
Элементы 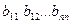 образуют главную диагональ матрицы.
образуют главную диагональ матрицы.
Элементы 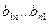 – побочную диагональ.
– побочную диагональ.
О2: Квадратная матрица, у которой вне главной диагонали стоят нули, называется диагональной.
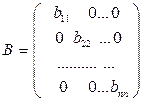
О3: Диагональная матрица, у которой на главной диагонали стоят 1, называется единичной.
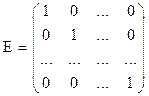
О4: Матрица размерности 1 × n называется матрица-строка.
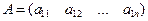
Матрица размерности m × 1 называется матрица-столбец.
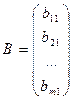
Операции над матрицами.
Сложение (вычитание) матриц.
Складывать можно только матрицы одной размерности. Сложение выполняется поэлементно:
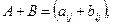
 .
.
Умножение матрицы на число.
Пусть λ произвольное действительное число. Для вычисления матрицы 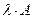 нужно каждый элемент матрицы А умножить на число λ.
нужно каждый элемент матрицы А умножить на число λ.
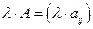
 ; λ
; λ  R
R
Транспонирование.
О: Транспонированной матрицей по отношению к матрице А называется матрица  , у которой строки поставлены в столбцы с соответствующими номерами.
, у которой строки поставлены в столбцы с соответствующими номерами.
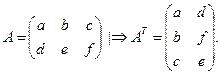
Умножение матриц.
О: Две матрицы А и В называются согласованными по умножению, если число столбцов первой матрицы равно числу строк второй матрицы.

Умножать можно только матрицы согласованные по умножению. Это действие выполняется по правилу:
а) первая строка первой матрицы умножается скалярно на 1й, 2й и т.д. столбцы второй матрицы и результаты записываются в первую строку;
б) вторая строка первой матрицы умножается скалярно на 1й , 2й и т.д. столбцы второй матрицы и результаты записываются во вторую строку;
… т.д.
Таким образом:
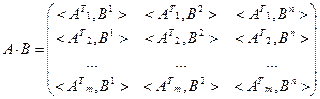
СЛАУ
О: Систему вида
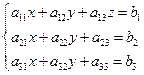 (1)
(1)
будем называть системой трёх уравнений с тремя неизвестными x, y и z.
Введём в рассмотрение следующие матрицы
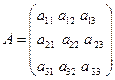
– матрица, составленная из коэффициентов системы (1).
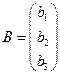
– матрица-столбец свободных членов системы (1).
О: Упорядоченная тройка чисел ( x0, y0, z0), при подстановке которой в систему (1) каждое уравнение обращается в верное равенство называется решением СЛАУ (1).
Метод Крамера решения СЛАУ.
Т. Крамера. Если ∆А≠0, то система (1) имеет единственное решение, которое находится по формулам:
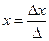 ;
; 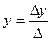 ;
; 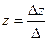 .
.
Здесь ∆=∆А,
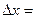
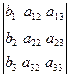 ;
; 
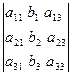 ;
; 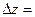
 .
.
Замечание. Если 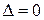 , то система является либо неоприделенной, либо несовместной.
, то система является либо неоприделенной, либо несовместной.
Если опредилитель однородной системы 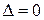 , то система сводится либо к двум неизвестным уравнениям(третье является их следствием), либо к одному (следствием которого являются остальные два уравнения). В обоих случиях однородная система имеет бесконечное множество решений.
, то система сводится либо к двум неизвестным уравнениям(третье является их следствием), либо к одному (следствием которого являются остальные два уравнения). В обоих случиях однородная система имеет бесконечное множество решений.
Практическая часть.
Пример 1. Придумать три матрицы размерности 4 ´ 3 и выполнить действия:
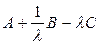 , где l = 3
, где l = 3

 Решение.
Решение.
Пусть 7 -8 13 14 31 -18
А = 12 -1 0 В = 11 -3 0
-2 51 4 4 5 -7
-2 9 -10 8 1 0
 |
13 2 5
С = 8 -9 1
0 3 1
2 -4 5

 14 31 -18
14 31 -18 
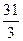 -6
-6
1) 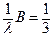 11 -3 0 =
11 -3 0 =  -1 0
-1 0
4 5 -7 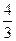

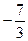
-8 1 0 
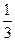 0
0
 |  |
13 2 5 39 6 15
2) lС = 3∙ 8 -9 1 = 24 -27 3
0 3 1 0 9 3
2 -4 5 6 -12 15
 |  |  | |||
7 -8 13 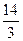
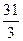 -6
-6 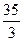
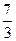 7
7
3) 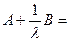 12 -1 0 +
12 -1 0 +  -1 0 =
-1 0 = 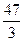 -2 0
-2 0
-2 51 4 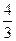

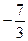
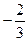
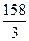

8 9 10 
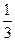 0
0 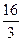
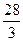 -10
-10
 | |||||
 | |||||
 | |||||
35 7 7 39 6 15 -82 -11 -8
3 3 3 3
4) А + 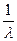 В –
В – 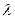 С =
С = 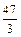 -2 0 – 24 -27 3 =
-2 0 – 24 -27 3 =  25 -3
25 -3
2 1585 0 9 3 -2 131 -4
3 3 3 3 3 3
1628 -10 6 -12 15 -2 64 -25
3 3 3 3
Пример 2. Придумать матрицы А 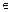 М3×3 ; В
М3×3 ; В 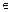 М3×3.
М3×3.
Найти: ВА, АВ, 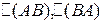 и сделать вывод
и сделать вывод
Решение.
Пусть  .
.
Найдем произведения ВА и АВ:


Посчитаем определители 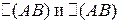 по правилу Саррюса:
по правилу Саррюса:
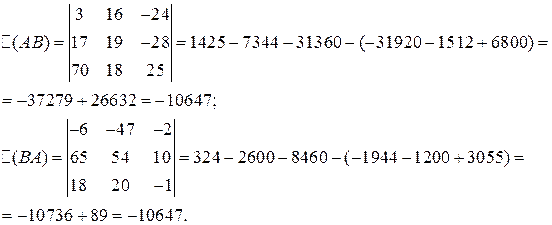
Вывод: 1) АВ ¹ ВА, т.е. для матриц коммутативный закон умножения, вообще говоря, неверен.
2) 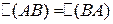 , т.е. определитель матрицы произведения не зависит от порядка умножения матриц.
, т.е. определитель матрицы произведения не зависит от порядка умножения матриц.
Пример 3. Решить неравенство, раскрыв определитель.

 3 4 -5
3 4 -5
х 7 -2 - 2 > 0
4 5 -2
Решение.
Раскрывая определитель, по правилу Саррюса, получим:
(168 + 5х – 16 + 70 – 6 – 48х) – 2 > 0.
Решим линейное неравенство:
- 43х + 214 > 0,
- 43х > - 214 | : (-43),
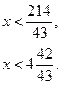
Ответ: 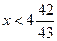 .
.
Пример 4. Решите систему методом Крамера 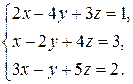
Решение.
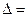
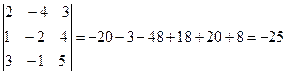 .
.
Т.к. ∆≠0, то система имеет единственное решение.

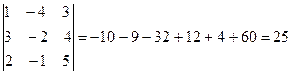 ;
;

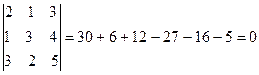 ;
;

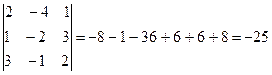 .
.
Итак, по формулам Крамера получаем:
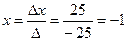 ;
; 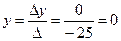 ;
;  .
.
Выполним проверку:
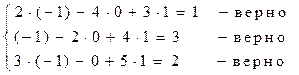
Ответ: (-1;0;1)
Числовые ряды
О: Числовым рядом называют выражение вида 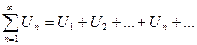 , где
, где 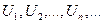 -члены ряда; Un –общий член ряда.
-члены ряда; Un –общий член ряда.
I. Схема исследования на сходимость положительных числовых рядов.
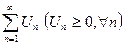
 |
- Выписать 3 первых члена ряда.
- Проверить выполнение необходимого условия сходимости (н.у.с.) ряда, т.е.
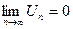
НУС выполнено НУС не выполнено
Продолжить исследования, Вывод: ряд расходится
Применив один из трёх признаков:
- признак сравнения
- признак Коши
- признак Даламбера
 |
Сделать вывод.
Т1: (признак сравнения) пусть ряды (1)  и (2)
и (2) 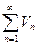 - положительные и
- положительные и 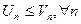
Тогда 1) если ряд (1) расходится, то ряд (2)-расходиться.
2) если ряд (2) сходится, то ряд (1)-сходиться.
Т2: (признак сравнения) пусть ряды (1)  и (2)
и (2) 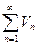 - положительные и существует
- положительные и существует  , тогда ряды (1) и (2) сходятся и расходятся одновременно.
, тогда ряды (1) и (2) сходятся и расходятся одновременно.
Замечание.
1) Удобно ввести сравнение с гармоническим рядом.
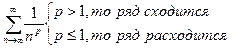
2) Формулы эквивалентности:
а) 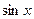 ~arcsinx~arctgx~ex-1~ln(x+1)~x,
~arcsinx~arctgx~ex-1~ln(x+1)~x, 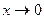
б) ax-1~xlna, 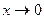
в) loga(1+x)~ 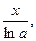
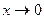
3) ”шкала роста функций”
ln n <<en<<n!<<nn, 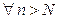

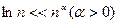 (*)
(*)
Т3: (признак Коши) Пусть ряд  -положительный и
-положительный и 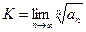 . Тогда:
. Тогда:
- Если К>1, то ряд расходится.
- Если К<1, то ряд сходится.
- Если К=1, то необходимы дополнительные исследования.
Т4: (признак Даламбера) Пусть ряд 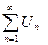 положительный и
положительный и 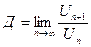 . Тогда:
. Тогда:
- Если Д<1, то ряд сходится.
- Если Д>1, то ряд расходится.
- Если Д=1, то необходимы дополнительные исследования.
II. Схема исследования знакочередующихся рядов.
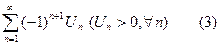
 |
- выписать 3-4 первых члена ряда.
-

 исследовать на абсолютную сходимость. Составить ряд из модулей
исследовать на абсолютную сходимость. Составить ряд из модулей 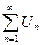 (4) и исследовать его на сходимость (см. схему исследования I.).
(4) и исследовать его на сходимость (см. схему исследования I.).
(4) сходится (4) расходится
Вывод: (3) сходится абсолютно Вывод для ряда (3)
нет абсолютной сходимости
 |
исследовать ряд (3) на условную сходимость, применив признак Лейбница
Т5: (признак Лейбница) Ряд 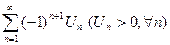 сходится, если:
сходится, если:
1. 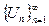 монотонно убывает, т.е.
монотонно убывает, т.е. 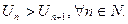
2. 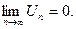
Функциональные ряды (степенной ряд).
О: Ряд вида  - называется степенным.
- называется степенным.
Замечание.
Ряд вида 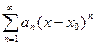 сводится к ряду (5) заменой
сводится к ряду (5) заменой 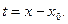
III. Схема исследования степенного ряда.

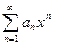
- Найти радиус сходимости степенного ряда по формулам:
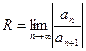 или
или 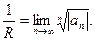
- Указать интервал сходимости ряда:
сходится
 |


 расходится расходится
расходится расходится
-R 0 R х
- Исследовать ряд на концах интервала сходимости, т.е. при х=R и х=-R.
- Записать ответ.
Замечание.
1. если R=0, то ряд (5) сходится только в точке х=0.
2. если 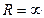 , то ряд (5) сходится всюду
, то ряд (5) сходится всюду 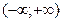 .
.
Практическая часть.
Пример 1.
Исследовать на сходимость положительный ряд.
А) 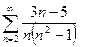
Решение.
Обратимся к схеме (I).
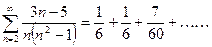
Проверим выполнение н.у.с.
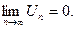
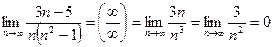 , т.е. н.у.с. выполнимо.
, т.е. н.у.с. выполнимо.
Продолжим исследование, применив признак сравнения (Т2).
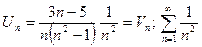 сходится, т.к. это гармонический ряд (р=2>1) I
сходится, т.к. это гармонический ряд (р=2>1) I 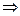 данный ряд сходится.
данный ряд сходится.
Б) 
Решение:
обратимся к схеме I.
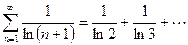
Проверим выполнение н.у.с.
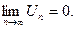
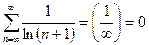 , т.е. н.у.с. выполнилось.
, т.е. н.у.с. выполнилось.
Продолжим исследование, применив признак сравнения (Т1).
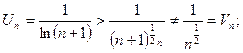
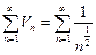 расходится как гармонический ряд с р=1/2<1
расходится как гармонический ряд с р=1/2<1 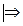 данный ряд расходится.
данный ряд расходится.
В) 
Решение:
Обратимся к схеме I.

Т.к. проверка н.у.с.
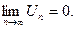
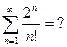 вызывает затруднение, то применим достаточный признак сравнения числового ряда, а именно признак Даламбера.
вызывает затруднение, то применим достаточный признак сравнения числового ряда, а именно признак Даламбера.
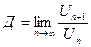

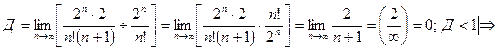 ряд сходится.
ряд сходится.
Пример 2. Исследовать ряд на условную и абсолютную сходимость.
А) 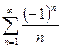
Решение: обратимся к схеме II.
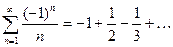
Исследуем ряд на абсолютную сходимость. Составим ряд из модулей.
 - расходится как гармонический с р=1.
- расходится как гармонический с р=1.
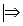 для данного ряда нет абсолютной сходимости.
для данного ряда нет абсолютной сходимости.
Исследуем ряд на условную сходимость. Применим признак Лейбница:
1) 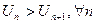 ;
; 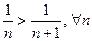
2) 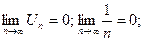
Т.к. условия признака Лейбница выполнены, то данный ряд сходится условно.
Пример 3. Найти радиус сходимости и интервал сходимости степенного ряда.
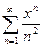
Решение: Обратимся к схеме III: т.к. 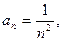 то
то
1) 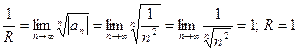
2) Интервал сходимости ряда:
сходится
 |


 расходится расходится
расходится расходится
-1 0 1 х
(-R;R)=(-1;1)
3) Исследуем сходимость ряда в точках x=-1 и х=1:
х=1
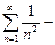 сходится как гармонический с р=2>1.
сходится как гармонический с р=2>1.
х=-1
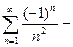 сходится абсолютно.
сходится абсолютно.
Ответ: R=1; интервал сходимости [-1;1]
I Основные понятия
О1: ДУ I-го порядка связывают независимую переменную х, искомую функцию y и её производную 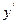 :
:
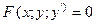 (1)
(1)
Если уравнение (1) можно разрешить относительно 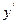 , то его записывают в виде:
, то его записывают в виде:
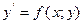
О2: Общим решением ДУ I-го порядка называется функция  j(х; с); содержащая одну производную постоянную и удовлетворяющая условиям:
j(х; с); содержащая одну производную постоянную и удовлетворяющая условиям:
1) функция j(х; с) является решением ДУ при каждом фиксированном с;
2) для любого начального условия  такое, что функция
такое, что функция 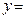 j(х; с0) удовлетворяют данному начальному условию.
j(х; с0) удовлетворяют данному начальному условию.
О3: Частным решением ДУ I-го порядка называется любая функция
у = j(х; с0), полученная из общего решения у=j(х;с) при конкретном значении постоянном с=с0.
IV Линейные ДУ
Общий вид: у’+p(x)y=q(x), где p(x), q(x) – заданные функции (3)
Метод решения: Решение ищется в виде произведения двух функций:
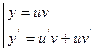 (4)
(4)
Ход решения: Подставляем соотношение (4) в уравнение (3):
u’v + uv’ + p(x)uv = q(x),
u’v + u[v’ + p(x)v] = q(x),
Пусть v такое, что [] = 0
v’ + p(x)v = 0,
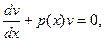
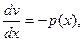


ln 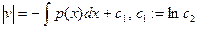
ln 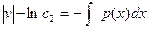 ,
,
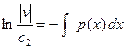 ,
,
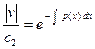
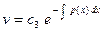 , c3=1
, c3=1
Итак:
v = 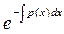
|
Подставим v в уравнение (5)
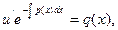
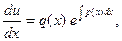
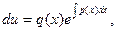

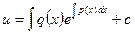
Т.к. 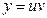 , то y=
, то y= 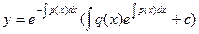
Замечание: уравнение Бернулли
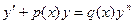
решается с помощью той же замены (4)
Практическая часть.
Пример 1. Найти общее решение уравнения 
Решение:
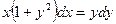 - ДУ с разделяющимися переменными.
- ДУ с разделяющимися переменными.
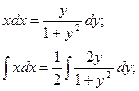
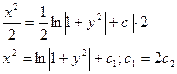
Выразим y: 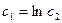
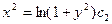
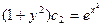
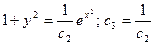

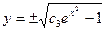
Ответ: 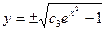
Пример 2. Найти частное решение уравнения 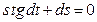 , удовлетворяющее начальному условию:
, удовлетворяющее начальному условию: 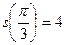
Решение:
 - ДУ с разделяющимися переменными.
- ДУ с разделяющимися переменными.
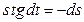
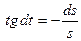
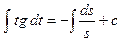
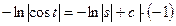
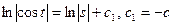
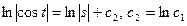
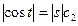
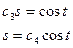
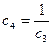 - общее решение ДУ.
- общее решение ДУ.
Воспользуемся начальными условиями:
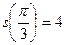
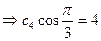
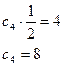
Подставим  в общее решение ДУ и получаем: s=8 cost- частное решение ДУ
в общее решение ДУ и получаем: s=8 cost- частное решение ДУ
Ответ: s=8 cost.
Пример 3. Найти общее решение ДУ 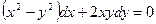
Решение:
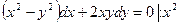
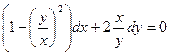
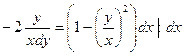
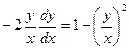
Замена: 
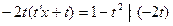
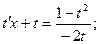
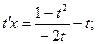
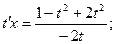
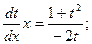
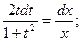
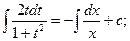
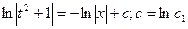
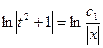
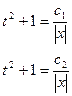
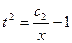
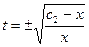
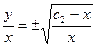
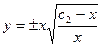 - общее решение ДУ.
- общее решение ДУ.
Ответ: 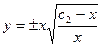
Пример 4. Найти общее решение ДУ 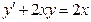
Решение: 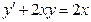 - линейное ДУ
- линейное ДУ
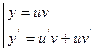
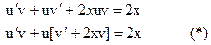
Пусть v такое, что 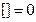

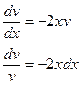
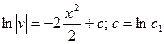
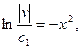
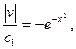
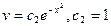
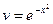
Подставляем v в уравнение (*)
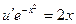
 Найдём:
Найдём: 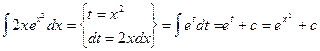
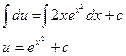
Т.к. y=uv, то 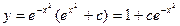
Ответ: y= 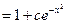
ТЕХНОЛОГИЧЕСКИЙ ИНСТИТУТ (ФИЛИАЛ) ДГТУ в г. Азове
Факультет среднего профессионального образования
Краткий конспект лекций
По дисциплине Математика
По специальности 15.02.08 Технология машиностроения
Составитель
Преподаватель первой категории
Н.М. Булда
Азов
2018
Теоретическая часть.
Дата: 2018-11-18, просмотров: 397.