О: Определителем (детерминантом) квадратной матрицы А называется число
DА ( det. А, |А|), которое находится по правилу:
1) 
2) 
; 
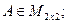
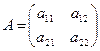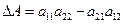
3) 
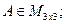
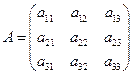
Определитель вычисляется по правилу Саррюса:
⊕ · · · · · · ⊖
· · · · · ·
· · · · · ·
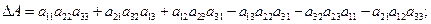
4) Общее правило вычисления определителей.
Определитель любого порядка можно вычислить, выполнив разложение по какой-нибудь строке или столбцу (удобно раскладывать по строке или столбцу содержащим нули),
т. е.
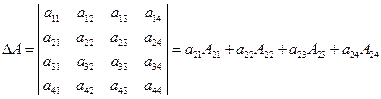
(разложение выполнено по второй строке), где 
– алгебраическое дополнение элемента 
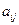, вычисляемое по правилу: 
.
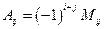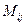(минор матрицы А) определитель матрицы, полученный из исходной, вычёркиванием 
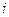-той строки и 
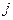-ого столбца.
Т. е.
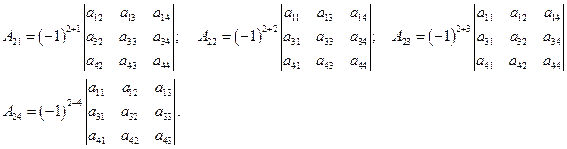
СЛАУ
О: Систему вида
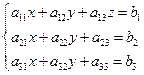(1)
будем называть системой трёх уравнений с тремя неизвестными x, y и z.
Введём в рассмотрение следующие матрицы
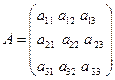
– матрица, составленная из коэффициентов системы (1).
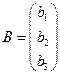
– матрица-столбец свободных членов системы (1).
О: Упорядоченная тройка чисел ( x0, y0, z0), при подстановке которой в систему (1) каждое уравнение обращается в верное равенство называется решением СЛАУ (1).
Метод Крамера решения СЛАУ.
Т. Крамера. Если ∆А≠0, то система (1) имеет единственное решение, которое находится по формулам:
; 
; 
.
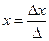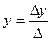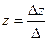Здесь ∆=∆А,
; 
; 
.
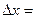
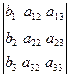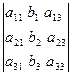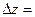
Замечание. Если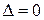 
, то система является либо неоприделенной, либо несовместной.
Если опредилитель однородной системы 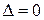, то система сводится либо к двум неизвестным уравнениям(третье является их следствием), либо к одному (следствием которого являются остальные два уравнения). В обоих случиях однородная система имеет бесконечное множество решений.
Практическая часть.
Пример 1. Придумать три матрицы размерности 4 ´ 3 и выполнить действия:
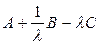, где l = 3
Решение.
Пусть 7 -8 13 14 31 -18
А = 12 -1 0 В = 11 -3 0
-2 51 4 4 5 -7
-2 9 -10 8 1 0
 |
13 2 5
С = 8 -9 1
0 3 1
2 -4 5
14 31 -18 
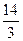
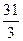-6
1) 
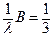11 -3 0 = 
-1 0
4 5 -7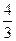 
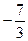
-8 1 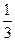0 
0
 |  |
13 2 5 39 6 15
2) lС = 3∙ 8 -9 1 = 24 -27 3
0 3 1 0 9 3
2 -4 5 6 -12 15
 |  |  | |||
7 -8 13 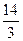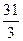-6 
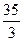
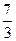7
3) 
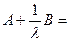12 -1 0 + -1 0 = 
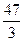-2 0
-2 51 4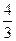 
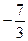
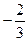
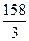
8 9 10 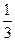0 
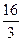
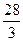-10
 | |||||
 | |||||
 | |||||
35 7 7 39 6 15 -82 -11 -8
3 3 3 3
4) А +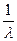 
В – 
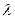С =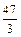 
-2 0 – 24 -27 3 = 
25 -3
2 1585 0 9 3 -2 131 -4
3 3 3 3 3 3
1628 -10 6 -12 15 -2 64 -25
3 3 3 3
Пример 2. Придумать матрицы А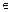 
М3×3 ; В 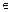М3×3.
Найти: ВА, АВ,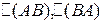 
и сделать вывод
Решение.
Пусть 
.
Найдем произведения ВА и АВ:
Посчитаем определители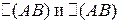 
по правилу Саррюса:
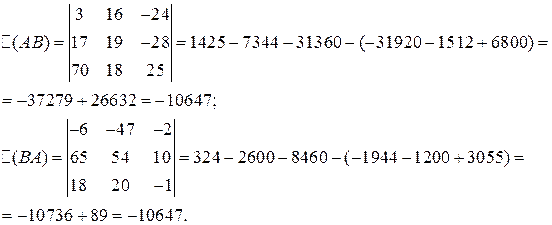
Вывод: 1) АВ ¹ ВА, т.е. для матриц коммутативный закон умножения, вообще говоря, неверен.
2) 
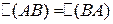, т.е. определитель матрицы произведения не зависит от порядка умножения матриц.
Пример 3. Решить неравенство, раскрыв определитель.
3 4 -5
х 7 -2 - 2 > 0
4 5 -2
Решение.
Раскрывая определитель, по правилу Саррюса, получим:
(168 + 5х – 16 + 70 – 6 – 48х) – 2 > 0.
Решим линейное неравенство:
- 43х + 214 > 0,
- 43х > - 214 | : (-43),
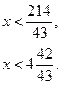
Ответ: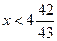 
.
Пример 4. Решите систему методом Крамера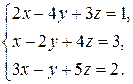 
Решение.
.
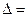
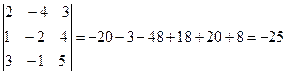Т.к. ∆≠0, то система имеет единственное решение.
;
;
.
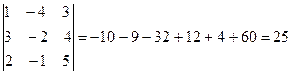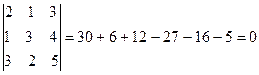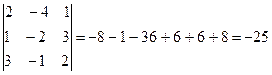Итак, по формулам Крамера получаем:
; 
; 
.
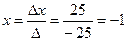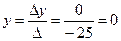Выполним проверку:
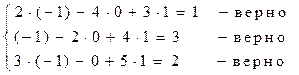
Ответ: (-1;0;1)
Тема: «Нахождение производных и дифференциалов высших порядков»
Дата: 2018-11-18, просмотров: 323.
