Поверка средств измерений - совокупность операций, выполняемых органами Государственной метрологической службы (другими уполномоченными на то органами, организациями) с целью определения и подтверждения соответствия средства измерений установленным техническим требованиям. Поверка средства измерений заключается в определении погрешностей средства измерений и в установлении его пригодности к применению. Проведение поверки позволяет установить, находятся ли метрологические характеристики средств измерений в заданных пределах.
Процедура поверки средств измерений регламентируется различными документами (государственными стандартами, инструкциями, методическими указаниями и др.), соблюдение требований которых обязательно
Калибровка средств измерений - совокупность операций, выполняемых с целью определения и подтверждения действительных значений характеристик и (или) пригодности к применению средств измерений, не подлежащих государственному метрологическому контролю и надзору.
Соподчинение Государственного эталона, вторичных, а также системы разрядных эталонов и рабочих средств измерений установлено государственной поверченной схемой.
Поверочная схема - утвержденный в установленном порядке документ, устанавливающий средства, методы и точность передачи размеров единиц от государственного эталона рабочим средствам измерений.
Поверочные схемы разделяют на государственные и локальные, Государственные поверочные схемы регламентируются государственными стандартами и распространяются на все средства измерений данного вида. Локальные поверочные схемы предназначены для метрологических служб Государственных органов управления и юридических лиц. Все локальные схемы должны соответствовать требованиям соподчиненности, которая определена государственной поверочной схемой.
Поверочные схемы состоят из чертежа и текстовой части. На чертеже указывают: наименование средств измерений, диапазоны значений физических величин, обозначения и значения погрешностей, наименования методов поверки. Текстовая часть состоит из вводной части и пояснений к элементам поверочной схемы.
Средства и методы измерений
Средство измерений (СИ) представляет собой техническое устройство, предназначенное для измерений и имеющее нормированные метрологические характеристики-
К средствам измерений относятся: меры, измерительные приборы, измерительные преобразователи, измерительные установки и измерительные системы.
Мера - это средство измерения, предназначенное для воспроизведения физической величины заданного размера. К мерам относят гири, концевые меры длины, нормальные элементы (меры ЭДС). Меры, воспроизводящие физическую величину одного размера (например, гиря, плоскопараллельная концевая мера длины), называются однозначными. Меры, воспроизводящие ряд одноименных величин различного размера (например, линейка с миллиметровыми делениями), называются многозначными
Широкое применение находят наборы и магазины мер. Указанное на мере (или приписанное мере) значение величины является номинальным значением меры. Разность между номинальным и действительным значениями меры называется погрешностью меры, которая является метрологической характеристикой меры.
Особую категорию средств измерений составляют стандартные образцы состава и свойств веществ и материалов. Например, образцы свойств: образец твердости, образец цвета и др., и образцы состава: чистые металлы, образцы марки стали, газовые смеси и др. Стандартный образец- средство измерений в виде вещества (материала), состав и свойства которого установлены при метрологической аттестации. В последние годы стандартные образцы нашли широкое применение в метрологической деятельности и в практике измерений.
Измерительный прибор - средство измерения, предназначенное для выработки сигнала измерительной информации в форме, доступной для непосредственного восприятия наблюдателем. Измерительные приборы по способу получения результата измерений подразделяют на показывающие (аналоговые и цифровые) и регистрирующие (самопишущие и печатающие). Для измерительных приборов обязательно должны быть нормированы:
· цена деления шкалы, пределы шкалы аналоговых приборов;
· выходной код, число его разрядов, номинальная цена единицы наименьшего разряда кода для цифровых приборов.
Кроме этих нормируются и другие характеристики, оказывающие влияние на результат измерения.
Измерительный преобразователь - средство измерения, предназначенное для выработки сигнала измерительной информации в форме, удобной для передачи, дальнейшего преобразования, обработки или хранения.
В отличие от измерительного прибора сигнал на выходе измерительного преобразователя не может восприниматься наблюдателем. Измеряемая величина, поступающая на измерительный преобразователь, называется входной, преобразованная - выходной.
Соотношение, устанавливающее связь между входной и выходной величинами, называется функцией преобразования измерительного преобразователя и является для него основной метрологической характеристикой. Функция преобразования может быть выражена формулой, графиком, таблицей.
Для категории средств измерений, охватывающей измерительные приборы и измерительные преобразователи, применяют термин "измерительное устройство".
Измерительная установка - совокупность функционально объединенных средств измерений (мер, измерительных приборов, измерительных преобразователей) и вспомогательных устройств, предназначенных для выработки сигналов измерительной информации в форме, удобной для непосредственного восприятия наблюдателем, и расположенных в одном месте.
Измерительная система - совокупность средств измерений (мер, измерительных приборов, измерительных преобразователей) и вспомогательных устройств, соединенных между собой каналами связей, предназначенных для выработки сигналов измерительной информации в форме, удобной для автоматической обработки передачи и (или) использования в автоматических системах управления.
По метрологическому назначению средства измерений подразделяют на два вида: рабочие средства измерений, которые предназначены для получения результатов измерений при решении различных производственных задач; эталоны, которые предназначены для воспроизведения, хранения и передачи размеров единиц рабочим средствам измерений.
Государственные и рабочие эталоны хранят и применяют Государственные научные метрологические центры. Эталоны (бывшие образцовые средства измерений) предназначены только для передачи размеров единиц, их хранят и применяют органы государственной метрологической службы и метрологические службы юридических лиц. Поэтому увязка рабочих средств измерений с Государственным эталоном является исключительно метрологической задачей и выполняют эту задачу аттестованные в установленном порядке специалисты.
Для получения результата измерения средства измерений применяются в соответствии с определенным методом.
Под методом измерений понимают совокупность приемов использования принципов и средств измерений.
Принципы измерения определяют совокупность физических явлений, на которых основаны измерения. Все методы измерения поддаются систематизации и обобщению по общим характерным признакам. Наибольшее распространение получила метрологическая классификация методов измерений, в соответствии с которой методы измерений подразделяются на метод непосредственной оценки и метод сравнения с мерой.
Метод непосредственной оценки - это такой метод измерений, при котором значение величины определяют непосредственно по отсчетному устройству измерительного прибора прямого действия. В приборе прямого действия предусмотрено преобразование сигнала измерительной информации в одном направлении без применения обратной связи. Например, измерение температуры ртутным термометром. Для измерения методом непосредственной оценки применяют очень много приборов различных видов: манометры, амперметры, расходомеры, барометры и др. Достоинствами этого метода является быстрота получения результата измерения, возможность непосредственного наблюдения за изменениями измеряемой величины. Однако его точностные возможности ограничены погрешностями градуировки прибора.
Метод сравнения с мерой - это такой метод, при котором измеряемую величину сравнивают с величиной, воспроизводимой мерой. При этом используют прибор сравнения- измерительный прибор, предназначенный для непосредственного сравнения измеряемой величины с известной. Метод сравнения с мерой имеет разновидности, которые часто рассматриваются как самостоятельные методы измерений: нулевой, дифференциальный и метод совпадений. Метод сравнения с мерой точнее метода непосредственной оценки. Точностные возможности метода сравнения с мерой определяются в основном погрешностью изготовления применяемых мер.
Отличием средства измерений от других технических устройств является то, что оно предназначено для получения измерительной информации и имеет нормированные метрологические характеристики.
Метрологические характеристики (м.х.) средств измерений-характеристики свойств средств измерений, оказывающие влияние на результаты и погрешности измерений. Эти характеристики называют еще точностными характеристиками средств измерении. Информация о назначении и метрологических характеристиках приведена в документации на средства измерений (в государственном стандарте, в ТУ, в паспорте на средство измерения).
Характерной особенностью измерительной техники является широкое распространение измерительных процессов, в которых одновременно участвуют несколько средств измерений, измеряющих разные физические величины и основанных на разных принципах действия. Это вызывает необходимость нормировать метрологические характеристики различных средств измерений на единой, принципиальной основе.
По метрологическим характеристикам средств измерений решается ряд задач, важных для обеспечения единства измерений:
-определение погрешности результата измерений (одной из составляющих погрешности измерений является погрешность средств измерений),
-выбор средств измерений по точности по известным условиям их применения и требуемой точности измерений (эта задача является обратной по отношению к задаче определения погрешности измерений);
-сравнение средств измерений различных типов с учетом условий их применения;
-замена одного средства измерений на другое - аналогичное;
оценка погрешности сложных измерительных систем и др.
Нормированные метрологические характеристики выражают в форме, удобной для обоснованного решения перечисленных выше задач и одновременно достаточно простого осуществления их контроля при поверке или калибровке.
При установлении совокупности нормируемых метрологических характеристик для средств измерений конкретного вида необходимо использовать номенклатуру характеристик, регламентированных ГОСТ 8.009-84 "ГСИ. Нормируемые метрологические характеристики средств измерений".
Например, в ГОСТ 8711-78 "Амперметры и вольтметры. Общие технические условия" нормируется предел допускаемой основной погрешности и нормальные условия; пределы допускаемых дополнительных погрешностей и рабочие области влияющих величин; предельно допускаемая вариация и невозвращения указателя нуля. При поверке или калибровке эти характеристики подлежат контролю.
В ГОСТ 8.009-84 установлены общие положения, комплекс метрологических характеристик средств измерений, и способы их нормирования- В этом стандарте приведены модели погрешности измерений в зависимости от свойств средств измерений, рекомендации по выбору метрологических характеристик для различных видов средств измерений и критерии существенности составляющих погрешности средств измерений. Положения и рекомендации стандарта могут быть использованы для оценивания инструментальной погрешности в реальных условиях применения средств измерений. ГОСТ 8.009-84 гармонизирован с международными рекомендациями.
В практике применения средств измерений широко используется выражение - класс точности. Это характеристика, зависящая от способа выражения пределов допускаемых погрешностей средств измерений. Впервые "класс точности" был введен в тридцатые годы применительно к стрелочным приборам и определял основную погрешность средств измерений (погрешность средств измерений в нормальных условиях). Введение класса точности преследовало цель классификации средств измерений по точности. Эта характеристика была удобной и для приборостроителей, т.к. позволила четко стандартизировать измерительные приборы в виде регламентированных рядов классов точности. Такое представление в то время было оправдано и характеристикой "класс точности" можно было руководствоваться при выборе средств измерений, при ориентировочной оценки точности измерений и др.
В настоящее время, когда схемы и конструкции средств измерений усложнились, а области применения средств измерений весьма расширились, на погрешность измерений стали существенно влиять и другие факторы. В частности, изменения внешних условий (температура окружающей среды, механические нагрузки на средства измерений и т.д.), а также характер изменения измеряемых величин во времени. Основная погрешность измерительных приборов перестала быть действительно основной составляющей погрешности измерений и класс точности не позволяет в полной мере решать практические задачи, перечисленные выше. Область практического применения характеристики "класс точности" ограничена только такими средствами измерений, которые предназначены для измерения статических величин. В международной практике "класс точности" устанавливается только для небольшой части приборов.
Требования к назначению, применению и обозначению "классов точности" регламентированы в ГОСТ 8.401-80 "ГСИ. Классы точности средств измерений. Основные положения". Этот стандарт гармонизирован с международными рекомендациями.
Метрологическое обеспечение средств измерений зависит от сферы их использования. Сферы распространения государственного метрологического контроля и надзора приведены в Законе РФ "Об обеспечении единства измерений" (ст. 13).
В сферах распространения государственного метрологического контроля и надзора используемые типы средств измерений должны быть утверждены и включены в Государственный реестр средств измерений, который ведет Всероссийский научно-исследовательский институт метрологической службы (ВНИИМС).
На средство измерений утвержденного типа и на эксплуатационные документы наносится знак утверждения типа установленной формы и выдается сертификат. Средства измерений при эксплуатации должны подвергаться периодической поверке органами Государственной метрологической службы или аккредитованны1ми метрологическими службами юридических лиц.
На поверенное средство измерений наносится клеймо и выдается свидетельство установленной формы. Перечни средств измерений, подлежащих поверке, составляются метрологическими службами юридических лиц и направляются в органы Государственной метрологической службы. При осуществлении Государственного метрологического надзора контролируется правильность и полнота этих перечней, а также состояние и применение средств измерений.
Средства измерений, применяемые вне сферы распространения государственного метрологического контроля и надзора, калибруются метрологической службой предприятия по эталонам, соподчиненным государственным эталонам единиц величин. Метрологические службы юридических лиц могут быть аккредитованы на право проведения калибровочных работ органами Государственной метрологической службы в Российской системе калибровки (РСК). Порядок аккредитации на право выполнения калибровочных работ устанавливается Госстандартом России.
Основные единицы СИ
Основные единицы СИ с указанием сокращенных обозначений русскими и латинскими буквами приведены в таблице.
| Величина | Единица | Сокращенное обозначение единицы | |
| русское | международное | ||
| Длина | метр | м | m |
| Масса | килограмм | кг | kg |
| Время | секунда | с | s |
| Сила эл. тока | ампер | А | А |
| Термодин. темп-ра | кельвин | К | К |
| Сила света | кандела | кд | cd |
| Кол-во вещества | моль | моль | mol |
Определения основных единиц, соответствующие решениям Генеральной конференции по мерам и весам, следующие.
Метр равен длине пути, проходимого светом в вакууме за 1/299792458 долю секунды.
Килограмм равен массе международного прототипа килограмма.
Секунда равна 9192631770 периодам излучения, соответствующего переходу между двумя сверхтонкими уровнями основного состояния атома цезия-133.
Ампер равен силе неизменяющегося тока, который при прохождении по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малой площади кругового сечения, расположенным на расстоянии 1 м один от другого в вакууме, вызывает на каждом участке проводника длиной 1 м силу взаимодействия, равную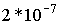 
Н.
Кельвин равен 1/273.16 части термодинамической температуры тройной точки воды.
Моль равен количеству вещества системы, содержащей столько же структурных элементов, сколько содержится атомов в углероде-12 массой 0.012 кг.
Кандела равна силе света в заданном направлении источника, испускающего монохроматическое излучение частотой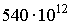 
Гц, энергетическая сила света которого в этом направлении составляет 1/683 Вт/ср.
Дополнительные единицы СИ
Международная система единиц включает в себя две дополнительные единицы - для измерения плоского и телесного углов.
Единица плоского угла - радиан (рад) - угол между двумя радиусами окружности, дуга между которыми по длине равна радиусу. В градусном исчислении радиан равен 57°17'48".
Стерадиан (ср), принимаемый за единицу телесного угла, - телесный угол, вершина которого расположена в центре сферы и который вырезает на поверхности сферы площадь, равную площа-ди квадрата со стороной, по длине равной радиусу сферы.
Измеряют телесные углы путем определения плоских углов и проведения дополнительных расчетов по формуле
.
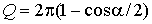где Q - телесный угол;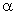 
- плоский угол при вершине конуса, образованного внутри сферы данным телесным углом.
Телесному углу 1 ср соответствует плоский угол, равный 65°32', углу 
ср - плоский угол 120°, углу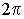 
ср - плоский угол 180°.
Дополнительные единицы СИ использованы для образования единиц угловой скорости, углового ускорения и некоторых других величин. Сами по себе радиан и стерадиан применяются в основном для теоретических построений и расчетов, так как большинство важных для практи-ки значений углов (полный угол, прямой угол и т.д.) в радианах выражаются трансцендентными числами ( ,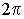 
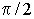и т.д.).
Производные единицы Международной системы единиц образуются с помощью простейших уравнений между величинами, в которых числовые коэффициенты равны единице. Так, для линейной скорости в качестве определяющего уравнения можно воспользоваться выражением для скорости рав-номерного прямолинейного движения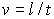 
.
При длине пройденного пути (в метрах) и времени t, за которое пройден этот путь (в секундах), скорость выражается в метрах в секунду (м/с). Поэтому единица скорости СИ - метр в секунду - это скорость прямолинейно и равномерно движущейся точки, при которой она за время 1 с перемещается на расстояние 1 м.
Если в определяющее уравнение входит числовой коэффициент, то для образования производной единицы в правую часть уравнения следует подставлять такие числовые значения исходных величин, чтобы числовое значение определяемой производной единицы было равно единице. Например, единица кинетической энергии СИ - килограмм-метр в квадрате на секунду в квадрате - это кинетическая энергия тела массой 2 кг, движущегося со скоростью 1 м/с, или кинетическая энергия тела массой 1 кг, движущегося со скоростью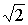 
м/с. Эта единица имеет особое наименование - джоуль (сокращенное обозначение Дж).
Системы физических величин
Физическая величина Х может быть при помощи математических действий выражена через другие физические величины А, В, С … уравнением вида:
Х= k АαВβСγ …,
где k - коэффициент пропорциональности; α, β, γ - показатели степени.
Формулы вида (2), выражающие одни физические величины через другие, называются уравнениями между физическими величинами. Коэффициент пропорциональности в таких уравнениях за редким исключением равен 1. Значение этого коэффициента не зависит от выбора единиц, а определяется только характером связи величин, входящих в уравнение.
Для каждой системы величин число основных величин должно быть вполне определенным и его стараются свести к минимуму. Основные величины могут выбираться произвольно, но важно, чтобы система была удобной для практического применения. Как правило, в качестве основных выбирают величины, характеризующие коренные свойства материального мира: длину, массу, время, силу, температуру, количество вещества и др. Каждой основной величине присвоен символ в виде прописной буквы латинского или греческого алфавита, называемой размерностью основной физической величины. Например, длина имеет размерность L, масса — М, время — Т, сила тока — I и т. д.
Понятие размерности вводится и для производной величины.
Размерностью производной физической величины называется выражение в форме степенного одночлена, составленного из произведений символов основных величин в различных степенях и отражающее связь данной физической величины с физическими величинами, принятыми в данной системе величин за основные, с коэффициентом пропорциональности, равным 1. Степени символов основных величин, входящих в одночлен, могут быт целыми, дробными, положительными и отрицательными в зависимости от связи рассматриваемой величины с основными. Связь производной величины через другие величины системы выражается определяющим уравнением производной величины. Размерность производной величины определяется путем подстановки в определяющее уравнение вместо входящих в него величин их размерностей. Причем, для этого используются простейшие уравнения связи, которые могут быть представлены в виде формулы (2). Например, если определяющим уравнением для скорости является уравнение v=s/t, где s — длина пути, пройденного за время t, то размерность скорости определяется по формуле L / T.
Форма уравнений, связывающих величины, не зависят от размеров единиц: какие бы единицы мы не выбирали, соотношения величин останутся неизменными и одинаковыми с соотношениями числовых значений. Этим свойством измерение отличается от всех других приемов оценки величин.
Размерность величин обозначается символом dim. В нашем случае размерность скорости будет выражена как
dim v = LT-1
Например, в системе величин LMT (длина, масса, время) размерность любой величины Х в общем виде будет выражаться формулой:
dim x = LlMmTt
где L, M, T — символы величин, принятых в качестве основных, в данном случае это длина, масса и время; l, m, t - показатели размерности производной величины х.
Размерность является более общей характеристикой, чем уравнение связи между величинами, т.к. одну и ту же размерность могут иметь величины разной природы, например, сила и кинетическая энергия.
Размерности имеют широкое практическое применение и позволяют:
· переводить единицы из одной системы в другую;
· проверять правильность расчетных формул;
· оценивать изменение размера производной величины при изменении размеров основных величин.
Шкалы измерений
Понятия физическая величина и измерение тесным образом связаны с понятием шкалы физической величины - упорядоченной совокупностью значений физической величины, служащей исходной основой для измерений данной величины.
Шкалой измерений называют порядок определения и обозначения возможных значений конкретной величины или проявлений какого-либо свойства. Понятия шкалы возникли в связи с необходимостью изучать не только количественные, но и качественные свойства природных и рукотворных объектов и явлений. Различают несколько типов шкал.
1. Шкала наименований (классификации) – это самая простая шкала, которая основана на приписывании объекту знаков или цифр для их идентификации или нумерации. Например, атлас цветов (шкала цветов) или шкала (классификация) растений Карла Линнея. Данные шкалы характеризуются только отношением эквивалентности (равенства) и в них отсутствуют понятия больше, меньше, отсутствуют единицы измерения и нулевое значение. Этот вид шкал приписывает свойствам объектов определенные числа, которые выполняют функцию имен. Процесс оценивания в таких шкалах состоит в достижении эквивалентности путем сравнения испытуемого образца с одним из эталонных образцов. Таким образом, шкала наименований отражает качественные свойства.
В шкале наименований (другое название этой шкалы - номинальная; это - переписанное русскими буквами английское название шкалы) допустимыми являются все взаимно-однозначные преобразования. В этой шкале числа используются лишь как метки. Примерно так же, как при сдаче белья в прачечную, т.е. лишь для различения объектов. В шкале наименований измерены, например, номера телефонов, автомашин, паспортов, студенческих билетов. Номера страховых свидетельств государственного пенсионного страхования, медицинского страхования, ИНН (индивидуальный номер налогоплательщика) измерены в шкале наименований. Пол людей тоже измерен в шкале наименований, результат измерения принимает два значения - мужской, женский. Раса, национальность, цвет глаз, волос - номинальные признаки. Номера букв в алфавите - тоже измерения в шкале наименований. Никому в здравом уме не придет в голову складывать или умножать номера телефонов, такие операции не имеют смысла. Сравнивать буквы и говорить, например, что буква П лучше буквы С, также никто не будет. Единственное, для чего годятся измерения в шкале наименований - это различать объекты. Во многих случаях только это от них и требуется. Например, шкафчики в раздевалках для взрослых различают по номерам, т.е. числам, а в
2. Шкала порядка (ранжирования) - упорядочивает объекты относительно какого-либо их свойства в порядке убывания или возрастания, например, землетрясений, силы ветра. Эти шкалы описывают уже количественные свойства. В данной шкале невозможно ввести единицу измерения, так как эти шкалы в принципе нелинейны. В ней можно говорить лишь о том, что больше или меньше, хуже или лучше, но невозможно дать количественную оценку во сколько раз больше или меньше.
В некоторых случаях в шкалах порядка может быть нулевая отметка. Например, в шкале Бофорта оценки силы ветра (отсутствие ветра). Примером шкалы порядка является также пятибалльная шкала оценки знаний учащихся. Ясно, что «пятерка» характеризует лучшее знание предмета, чем «тройка», но во сколько раз лучше, сказать невозможно.
Другими примерами шкалы порядка являются шкала силы землетрясений (например, шкала Рихтера), шкалы твердости, шкалы силы ветра. Некоторые из этих шкал имеют эталоны, например, шкалы твердости материалов. Другие шкалы не могут их иметь, например, шкала волнения моря.
Почему мнения экспертов естественно выражать именно в порядковой шкале? Как показали многочисленные опыты, человек более правильно (и с меньшими затруднениями) отвечает на вопросы качественного, например, сравнительного, характера, чем количественного. Так, ему легче сказать, какая из двух гирь тяжелее, чем указать их примерный вес в граммах.
В различных областях человеческой деятельности применяется много других видов порядковых шкал. Так, например, в минералогии используется шкала Мооса, по которому минералы классифицируются согласно критерию твердости. А именно: тальк имеет балл 1, гипс - 2, кальций - 3, флюорит - 4, апатит - 5, ортоклаз - 6, кварц - 7, топаз - 8, корунд - 9, алмаз - 10. Минерал с большим номером является более твердым, чем минерал с меньшим номером, при нажатии царапает его.
Порядковыми шкалами в географии являются - бофортова шкала ветров ("штиль", "слабый ветер", "умеренный ветер" и т.д.), шкала силы землетрясений. Очевидно, нельзя утверждать, что землетрясение в 2 балла (лампа качнулась под потолком - такое бывает и в Москве) ровно в 5 раз слабее, чем землетрясение в 10 баллов (полное разрушение всего на поверхности земли).
В медицине порядковыми шкалами являются - шкала стадий гипертонической болезни (по Мясникову), шкала степеней сердечной недостаточности (по Стражеско-Василенко-Лангу), шкала степени выраженности коронарной недостаточности (по Фогельсону), и т.д. Все эти шкалы построены по схеме: заболевание не обнаружено; первая стадия заболевания; вторая стадия; третья стадия… Иногда выделяют стадии 1а, 1б и др. Каждая стадия имеет свойственную только ей медицинскую характеристику. При описании групп инвалидности числа используются в противоположном порядке: самая тяжелая - первая группа инвалидности, затем - вторая, самая легкая - третья.
Номера домов также измерены в порядковой шкале - они показывают, в каком порядке стоят дома вдоль улицы. Номера томов в собрании сочинений писателя или номера дел в архиве предприятия обычно связаны с хронологическим порядком их создания.
При оценке качества продукции и услуг, в т.н. квалиметрии (буквальный перевод: измерение качества) популярны порядковые шкалы. А именно, единица продукции оценивается как годная или не годная. При более тщательном анализе используется шкала с тремя градациями: есть значительные дефекты - присутствуют только незначительные дефекты - нет дефектов. Иногда применяют четыре градации: имеются критические дефекты (делающие невозможным использование) - есть значительные дефекты - присутствуют только незначительные дефекты - нет дефектов. Аналогичный смысл имеет сортность продукции - высший сорт, первый сорт, второй сорт,…
При оценке экологических воздействий первая, наиболее обобщенная оценка - обычно порядковая, например: природная среда стабильна - природная среда угнетена (деградирует). Аналогично в эколого-медицинской шкале: нет выраженного воздействия на здоровье людей - отмечается отрицательное воздействие на здоровье.
Порядковая шкала используется и во многих иных областях. В эконометрике это прежде всего различные методы экспертных оценок (см. посвященную им главу 12).
Все шкалы измерения делят на две группы - шкалы качественных признаков и шкалы количественных признаков.
Порядковая шкала и шкала наименований - основные шкалы качественных признаков. Поэтому во многих конкретных областях результаты качественного анализа можно рассматривать как измерения
Шкалы порядка и наименований называют неметрическими шкалами.
Шкалы количественных признаков - это шкалы интервалов, отношений, разностей, абсолютная.
3. Шкала интервалов (разностей) содержит разность значений физической величины.
По шкале интервалов измеряют величину потенциальной энергии или координату точки на прямой. В этих случаях на шкале нельзя отметить ни естественное начало отсчета, ни естественную единицу измерения. Исследователь должен сам задать точку отсчета и сам выбрать единицу измерения.
Допустимыми преобразованиями в шкале интервалов являются линейные возрастающие преобразования, т.е. линейные функции. Температурные шкалы Цельсия и Фаренгейта связаны именно такой зависимостью: 0С = 5/9 (0F - 32), где 0С - температура (в градусах) по шкале Цельсия, а 0F - температура по шкале Фаренгейта.Для этих шкал имеют смысл соотношения эквивалентности, порядка, суммирования интервалов (разностей) между количественными проявлениями свойств.
Шкала состоит из одинаковых интервалов, имеет условную (принятую по соглашению) единицу измерения и произвольно выбранное начало отсчета - нуль. Примером такой шкалы являются различные шкалы времени, начало которых выбрано по соглашению (от Рождества Христова, от переселения пророка Мухаммеда из Мекки в Медину). Другими примерами шкалы интервалов являются шкала расстояний и температурная шкала Цельсия. Результаты измерений по этой шкале (разности) можно складывать и вычитать.
4. Шкала отношений - это шкала интервалов с естественным (не условным) нулевым значением и принятые по соглашению единицы измерений. В ней нуль характеризует естественное нулевое количество данного свойства. Например, абсолютный нуль температурной шкалы. Это наиболее совершенная и информативная шкала. Результаты измерений в ней можно вычитать, умножать и делить. В некоторых случаях возможна и операция суммирования для аддитивных величин. Аддитивной называется величина, значения которой могут быть суммированы, умножены на числовой коэффициент и разделены друг на друга (например, длина, масса, сила и др.). Неаддитивной величиной называется величина, для которой эти операции не имеют физического смысла, например, термодинамическая температура. Примером шкалы отношений является шкала масс – массы тел можно суммировать, даже если они не находятся в одном месте. Из количественных шкал наиболее распространенными в науке и практике являются шкалы отношений. В них есть естественное начало отсчета - нуль, т.е. отсутствие величины, но нет естественной единицы измерения. По шкале отношений измерены большинство физических единиц: масса тела, длина, заряд, а также цены в экономике. Допустимыми преобразованиями шкале отношений являются подобные (изменяющие только масштаб). Другими словами, линейные возрастающие преобразования без свободного члена. Примером является пересчет цен из одной валюты в другую по фиксированному курсу. Предположим, мы сравниваем экономическую эффективность двух инвестиционных проектов, используя цены в рублях. Пусть первый проект оказался лучше второго. Теперь перейдем на валюту самой экономически мощной державы мира - юани, используя фиксированный курс пересчета. Очевидно, первый проект должен опять оказаться более выгодным, чем второй. Это очевидно из общих соображений. Однако алгоритмы расчета не обеспечивают автоматически выполнения этого очевидного условия. Надо проверять, что оно выполнено. Результаты подобной проверки для средних величин описаны ниже.
.
5. Абсолютные шкалы - это шкалы отношений, в которых однозначно (а не по соглашению) присутствует определение единицы измерения. Абсолютные шкалы присущи относительным единицам (коэффициенты усиления, полезного действия и др.), единицы таких шкал являются безразмерными.
6. Условные шкалы - шкалы, исходные значения которых выражены в условных единицах. К таким шкалам относятся шкалы наименований и порядка.
Шкалы разностей, отношений и абсолютные называются метрическими (физическими) шкалами.
В шкале разностей есть естественная единица измерения, но нет естественного начала отсчета. Время измеряется по шкале разностей, если год (или сутки - от полудня до полудня) принимаем естественной единицей измерения, и по шкале интервалов в общем случае. На современном уровне знаний естественного начала отсчета указать нельзя. Дату сотворения мира различные авторы рассчитывают по-разному, равно как и момент рождества Христова. Так, согласно новой статистической хронологии, разработанной группой акад. РАН А.Т.Фоменко, Господь Иисус Христос родился примерно в 1054 г. по принятому ныне летоисчислению в Стамбуле (он же - Царьград, Византия, Троя, Иерусалим, Рим).
Только для абсолютной шкалы результаты измерений - числа в обычном смысле слова. Примером является число людей в комнате. Для абсолютной шкалы допустимым является только тождественное преобразование.
В процессе развития соответствующей области знания тип шкалы может меняться. Так, сначала температура измерялась по порядковой шкале (холоднее - теплее). Затем - по интервальной (шкалы Цельсия, Фаренгейта, Реомюра). Наконец, после открытия абсолютного нуля температуру можно считать измеренной по шкале отношений (шкала Кельвина). Надо отметить, что среди специалистов иногда имеются разногласия по поводу того, по каким шкалам следует считать измеренными те или иные реальные величины. Другими словами, процесс измерения включает в себя и определение типа шкалы (вместе с обоснованием выбора определенного типа шкалы). Кроме перечисленных шести основных типов шкал, иногда используют и иные шкалы.
Дата: 2018-11-18, просмотров: 435.
