Мультипликативная погрешность – погрешность чувствительности, возрастает или убывает с ростом измеряемой величины.

Аддитивная погрешность – погрешность нуля, остается постоянной во всем диапазоне измерений.

2.3 Обработка результатов прямых многократных равноточных измерений

Равноточными называются измерения, у которых все значения отсчетов 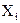 имеют одинаковую дисперсию (точность).

Обработка результатов многократных равноточных измерений производится в следующем порядке:

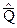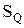- Определение оценок числовых характеристик  и  закона распределения вероятности результата измерения (  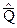и 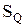 – среднее арифметическое и оценка среднего квадратического отклонения измеряемой величины соответственно);

- Исключение «грубых промахов», если таковые имеются, из результатов измерений и пересчет оценок числовых характеристик закона распределения вероятности результата измерения;

- Проверка гипотезы о виде закона распределения вероятности результата измерения (чаще всего проверяется гипотеза о его нормальности);

- Представление результата измерения в виде доверительного интервала, соответствующего определенному уровню доверительной вероятности.

Определение оценок числовых характеристик закона распределения вероятности результата измерений

Числовые характеристик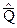и  и 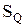 определяются по формулам:

                                       ,                                                 

                                  ,                                            

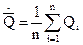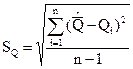где Q_i – результат i-того параллельного наблюдения (измерения);

n – число параллельных наблюдений (измерений).

При проведении расчетов числовых характеристик и других параметров всегда встает вопрос о точности их вычисления, т.е. о том с каким числом значащих цифр записывать полученные значения. При обработке результатов измерений следует руководствоваться следующими правилами:

1. Значение оценок средних квадратических отклонений  и 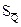 может быть определено максимум с двумя значащими цифрами, причем вторую значащую цифру следует округлять до 0 или 5. Под значащими цифрами понимается всякая отличная от нуля цифра десятичной записи числа и нуль, если он находится между значащими цифрами или является представителем сохраненного десятичного разряда. Например, у приближенного числа 0,002080 подчеркнутые нули не являются значащими цифрами, т. к. они указывают только порядок числа (10^–3). Остальные два нуля являются значащими цифрами, т. к. первый из них находится между значащими цифрами 2 и 8, а второй указывает, что округленное число отличается от неокругленного менее чем на ±5 единиц седьмого разряда;

2. Для предотвращения накопления погрешности промежуточных расчетов среднее квадратическое отклонение 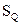 следует определять как минимум с одной запасной значащей цифрой, т.е. с 3-мя значащими цифрами, округляя его при окончательной записи до двух значащих цифр, как было указано в п. 1. Таким же образом следует поступать с любыми промежуточными данными;

3. Среднее арифметическое 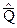 следует рассчитывать с таким количеством знаков после запятой, которое соответствует последней значащей цифре среднего квадратического отклонения среднего арифметического  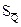после его округления (окончательной записи). Например: если по расчетам среднее квадратическое отклонение среднего арифметического получилось 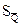=0,0273, то его следует округлить до значения 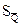=0,025, а среднее арифметическое  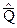необходимо определять до третьего знака после запятой.

В дальнейшем для построения доверительного интервала понадобится еще оценка среднего квадратического отклонения 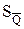 среднего арифметического значения :

                                        .                                                  

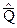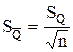Окончательное определение среднего арифметического 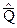 и оценок средних квадратических отклонений самой измеряемой величины  и ее среднего арифметического значения 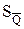 осуществляется только после исключения грубых промахов.

Исключение грубых промахов

Существует несколько способов проверки гипотезы о наличии грубых промахов в результате измерений. Наиболее распространенными являются: проверка наличия грубых промахов с помощью n-критерия и с помощью правила «трех сигм».

1.Проверка гипотезы о наличии грубых промахов в результате измерений с помощью n-критерия.

Этот способ применяется при малом числе измерений 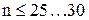, если их вероятность распределена по нормальному закону. Из всех полученных значений измеряемой величины на наличие грубых промахов проверяют, как правило, минимальный  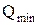и максимальный  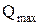результаты. Если они не содержат грубых погрешностей, то промежуточные результаты тем более. При проверке сначала рассчитывают значения n-критерия, соответствующие максимальному и минимальному результатам измерений:

                                    ,                                              

                                     .                                              

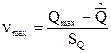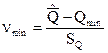Если значение 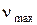 или 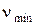 больше критического 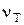, выбираемого из таблицы значений n при различных числах измерений n, то один или оба проверяемых результата измерений являются грубыми промахами, т.е. содержат грубые погрешности. Критическое значение  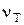выбирается, исходя из уровня доверительной вероятности Р (уровня значимости, равного 1 – Р) и числа результатов измерений n.

Грубые промахи исключаются из экспериментальных данных (отбрасываются), значения параметров 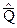 и 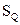 пересчитываются заново, после чего опять проводится аналогичная проверка и так до тех пор, пока все гру­бые промахи не будут отброшены. После исключения грубых промахов окончательно определяются значения  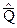и .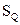

2. Проверка гипотезы о наличии грубых промахов в результате измерений с помощью правила «трех сигм»

Данный способ проверки наличия грубых промахов менее надежен, чем предыдущий и применяется, как правило, при соблюдении следующих условий:

1. Закон распределения вероятности результатов измерений соответствует нормальному;

2. Число измерений больше 25 … 30, т.е.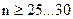

3. Числовые характеристики закона распределения вероятности известны достаточно точно.

Для проведения данной проверки сначала вычисляют значения 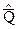 и 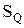. Далее определяют допустимые значения  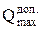и 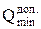 измеряемой величины, которые с доверительной вероятностью Р = 0,9973 еще не являются грубыми промахами:

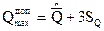
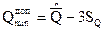
Все значения измеряемой величины, выходящие за пределы интервала 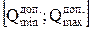 признаются грубыми промахами с вероятностью Р = 0,9973.

После отбрасывания грубых промахов необходимо пересчитать значения 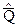 и 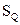 и повторять проверку до тех пор, пока все грубые промахи не будут исключены из результата измерений. В дальнейших расчетах используются числовые характеристик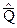и  и 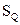 закона распределения вероятности, рассчитанные для результата измерений, не содержащего грубых промахов.

Выявление вида закона распределения вероятности результата измерения .

Проверка нормальности распределения результатов измерений при малом числе измерений

При малом числе наблюдений 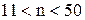 обычно проверяют соответствие распределения вероятности нормальному закону. При этом используют специализированные критерии, годные для проверки гипотезы о соответствии только одному конкретному закону распределения вероятности. В большинстве случаев таким законом и является нормальный закон. Поскольку в данной ситуации рассматривается только одна гипотеза (о нормальности закона распределения вероятности), то специальных действий по обоснованию ее выдвижения обычно не производят, что, тем не менее, не исключает возможности предварительного исследования эмпирического закона распределения вероятности результата измерения с последующим выдвижением той или иной гипотезы о виде этого закона.

Чаще всего гипотеза о нормальности распределения результатов измерений при малом их числе проверяется с помощью составного критерия, который в свою очередь состоит из двух критериев.

Первый критерий основан на вычислении статистики:

                         ,                                   

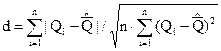квантили распределения которой приведены в таблице квантилей распределения статистики d [1]. Гипотеза о нормальности на основании первого критерия принимается, если при данном числе измерений n и выбранном уровне значимости 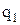 соблюдается условие:

                                  ,                                           

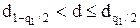где q₁ – уровень значимости при проверке гипотезы по первой части критерия;

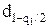 и 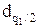 квантили, выбираемые по таблице квантилей распределения статистики d.

На основании второго критерия гипотеза о нормальности распределения принимается, если не более m разностей 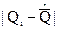 превосходят уровень 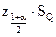, где 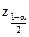 – квантиль интегральной функции нормированного нормального распределения, определяемая по данным таблицы интегральной функции нормированного нормального распределения при значении:

                                    .                                             

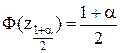Величина a находится при заданном уровне значимости  второго критерия по данным таблицы значений m и a, соответствующим различным величинам параметров n и q₂.

Распределение вероятности результатов измерений считается отличным от нормального, если не выполняется хотя бы один из этих двух критериев. Уровень значимости составного критерия определяется по формуле:

                                       .                                                

Это значит, что гипотеза о нормальности распределения вероятности результата измерения принимается или отвергается с уровнем значимости q или доверительной вероятностью Р = 1 – q.

Проверка нормальности распределения результатов измерений при большом числе измерений

При большом числе измерений 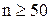 для выявления вида закона распределения вероятности чаще используют универсальные критерии, с помощью которых можно проверять гипотезу о соответствии любому виду распределения. Поскольку заранее не известно, какой из возможных законов лучше описывает эмпирическое распределение вероятности результата измерения, необходимо предварительно исследовать полученный закон и уже на основании этого исследования выдвинуть гипотезу о виде распределения вероятности.

Такое предварительное исследование производят чаще всего с помощью гистограммы. По ее виду можно предположить, какой теоретический закон распределения вероятности лучше соответствует данной гистограмме, т.е. эмпирическому распределению, полученному при измерении.

После выдвижения гипотезы о виде закона распределения вероятности результата измерений осуществляют проверку ее непротиворечивости (правдивости или правильности) с помощью какого-либо критерия согласия. Наиболее распространенным критерием является критерий 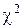 Пирсона. При использовании этого критерия за меру расхождения экспериментальных данных с теоретическим законом распределения вероятности результата измерений принимается сумма квадратов отклонений частостей  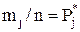от теоретической вероятности  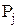попадания отдельного результата измерений в j-ый интервал, причем, каждое слагаемое берется с весовым коэффициентом :

                  ,                           

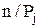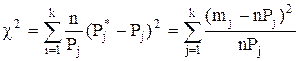где 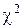 критерий Пирсона;

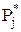 – частость или экспериментальное значение вероятности попадания результата измерений в j-ый интервал:

                                         ;                                                   

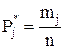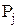 – теоретическая вероятность попадания результата измерений в i-ый интервал (рассчитывается или определяется по таблице с принятой гипотезой о виде закона распределения вероятности результата измерений).

Проверка нормальности закона распределения вероятности результата измерений согласно критерию 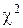 сводится к следующему:

1. Данные наблюдений группируют по интервалам, как при построении гистограммы, и подсчитывают частоты 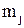. Если в некоторые интервалы попадает менее пяти наблюдений, то такие интервалы объединяются с соседними. При этом соответственно уменьшается число степеней свободы:

                                         ,                                                  

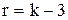где k – число интервалов гистограммы после объединения.

2. Принимают величины 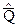 и 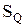, рассчитанные по формулам (2.1) и (2.2) в качестве параметров теоретического закона распределения вероятности результата измерений.

3. Для каждого интервала находят вероятности попадания в них результатов наблюдений по таблице нормированного нормального распределения вероятности:

                      ,                               

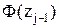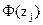где:  и  – значения интегральной функции нормированного нормального распределения (выбирается по таблице интегральной функции нормированного нормального распределения) в начале и конце i-го интервала соответственно;

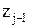 и 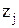 – значения аргумента интегральной функции распределения вероятности, соответствующие границам i-го интервала:

                            ; ,                                      

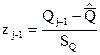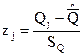где 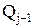,  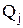– начало и конец i-го интервала.

4. Для каждого интервала вычисляют значение 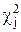 критерия Пирсона:

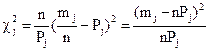
и суммируют эти значения для всех k интервалов, т.е.:

                                        .

5. Исходя из числа степеней свободы и уровня значимости 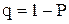 (Р – вероятность, с которой принимается или отвергается выдвинутая гипотеза) определяют по таблице интегральной функции 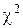-распределения Пирсона допустимое (критическое) значение .

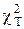Если 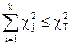, то гипотеза о нормальности закона распределения вероятности результата измерений принимается с доверительной вероятностью Р. В противном случае гипотеза с той же вероятностью отвергается.

Примечание:

1. При определении числа степеней свободы r следует иметь в виду, что k – это число интервалов, оставшихся после их объединения, если таковое было.

- Доверительную вероятность Р принимают обычно на уровне 0,9…0,95, т.е. Р = 0,9…0,95

Представление результата в принятой форме

Обычно принято результат любого измерения представлять в виде доверительного интервала с доверительной вероятностью попаданий в него результата измерений Q:

                                 ,                                          

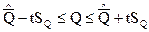где t – относительная ширина доверительного интервала, зависящая от вероятности Р и вида закона распределения вероятности результата измерений;

Q – истинное значение измеряемой величины.

При многократном измерении в качестве меры рассеяния результата используют оценку среднего квадратического отклонения среднего арифметического значения 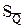. Поэтому доверительный интервал примет вид:

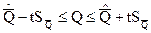
Относительная ширина доверительного интервала t выбирается по-разному в зависимости от числа измерений n. Если измерений мало, т.е. 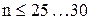, то параметр t выбирается по таблицам распределения Стьюдента, а если достаточно много, т.е.  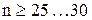то по таблицам нормированного нормального распределения.

Следует иметь в виду, что законы распределения вероятности величин Q и 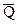 могут не совпадать между собой. Поэтому в общем случае, если неизвестен закон распределения вероятности величины 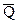, относительную ширину интервала t определяют из неравенства Чебышева:

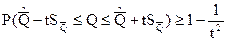
или

                       ,                                

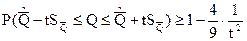если известно, что этот закон симметричен.

Если же известно, что вероятность величины 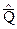 подчиняется нормальному закону, что обычно и бывает при нормальном распределении вероятности результатов Q_i, то пользуются таблицей нормированного нормального распределения вероятности.