| Число | Собственные числа | ||||
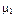
| 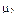
| 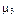
| 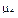
| 
| |
| 4 | 2,4674 | 22,217 | 65,459 | 222,51 | — |
| 5 | 2,4674 | 22,207 | 61,696 | 139,45 | 409,02 |
| Точные Значения [49] | 2,4674 | 22,207 | 61,685 | 120,90 | 199,86 |
Отметим, что последние собственные числа как в четвертом, так и пятом приближениях почти в два раза отличаются от точных их значений. При использовании дополнительных граничных условий, даже если не требовать ортогональности невязки к собственной функции, получаются значительно более точные значения собственных чисел, а при выполнении ортогональности невязки – они практически совпадают с точными, причем, первое и второе собственные числа – с точностью соответственно до десятого и шестого
знака после запятой. Этот факт можно объяснить тем, что при совместном использовании точных и приближенных аналитических методов без применения дополнительных граничных условий собственные числа определяются из системы алгебраических линейных уравнений, матрицы которых, являясь заполненными квадратными матрицами с большим разбросом коэффициентов по абсолютной величине, при большом числе приближений, как правило, оказываются плохо обусловленными. В связи с чем, получаемые решения могут существенно отличаться от точных и особенно при малых значениях числа Фурье.
Главное отличие изложенного выше метода с использованием дополнительных граничных условий состоит в том, что в системе алгебраических линейных уравнений относительно неизвестных коэффициентов 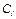 (
( 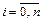 ) бóльшая часть уравнений разделяются (в одно уравнение входит лишь один неизвестный коэффициент) и, таким образом, легко может быть найдена бóльшая часть неизвестных коэффициентов. Относительно оставшихся коэффициентов в общем виде приходится решать лишь два-три алгебраических линейных уравнения, независимо от числа приближений. В результате система алгебраических уравнений при любом числе приближений решается на точном аналитическом уровне. Основную трудность здесь представляет нахождение решения характеристического уравнения относительно собственных чисел краевой задачи, степень которого с увеличением числа приближений возрастает. Математические методы решения таких уравнений разработаны. Ниже (см. § 6.2) будет показано, что решениями этих уравнений являются собственные числа краевых задач Штурма-Лиувилля.
) бóльшая часть уравнений разделяются (в одно уравнение входит лишь один неизвестный коэффициент) и, таким образом, легко может быть найдена бóльшая часть неизвестных коэффициентов. Относительно оставшихся коэффициентов в общем виде приходится решать лишь два-три алгебраических линейных уравнения, независимо от числа приближений. В результате система алгебраических уравнений при любом числе приближений решается на точном аналитическом уровне. Основную трудность здесь представляет нахождение решения характеристического уравнения относительно собственных чисел краевой задачи, степень которого с увеличением числа приближений возрастает. Математические методы решения таких уравнений разработаны. Ниже (см. § 6.2) будет показано, что решениями этих уравнений являются собственные числа краевых задач Штурма-Лиувилля.
| 
| 
|
Рис. 6.3 Изменение не- вязки уравнения (4.1) для 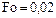
| Рис. 6.4 Изменение невязки уравнения (4.1) для 
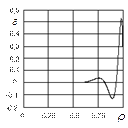
| Рис. 6.5 Изменение невязки начального условия |
На графиках рис. 6.3, 6.4 дано изменение невязки 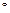 уравнения (6.1) для пяти членов ряда (6.22). Из анализа графиков следует, что при
уравнения (6.1) для пяти членов ряда (6.22). Из анализа графиков следует, что при 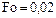 в диапазоне
в диапазоне 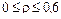 уравнение (6.1) удовлетворяется точно. Максимальная невязка имеет место вблизи точки
уравнение (6.1) удовлетворяется точно. Максимальная невязка имеет место вблизи точки  . Невязка уравнения (6.1) в точке
. Невязка уравнения (6.1) в точке 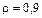 для
для 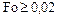 становится практически равной нулю (рис. 6.4).
становится практически равной нулю (рис. 6.4).
Максимальная невязка начального условия 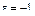 (рис. 6.5) при
(рис. 6.5) при 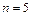 наблюдается в точке
наблюдается в точке 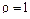 . Это объясняется тем, что в точке
. Это объясняется тем, что в точке 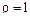 в любой момент времени выполняется граничное условие 1-го рода. С увеличением числа приближений невязка начального условия уменьшается за исключением точки
в любой момент времени выполняется граничное условие 1-го рода. С увеличением числа приближений невязка начального условия уменьшается за исключением точки 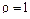 , где она всегда равна
, где она всегда равна 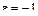 .
.
Дата: 2018-11-18, просмотров: 380.