Изучение любого физического процесса методами математики сводится к установлению аналитических зависимостей между величинами, характеризующими это явление. Для сложных физических процессов, в которых определяющие величины изменяются в пространстве и времени, установить зависимость между этими величинами не всегда возможно. В этих случаях используются методы математической физики, с использованием которых рассматривается протекание процесса не во всем изучаемом пространстве, а в некотором объеме вещества и в течение элементарного отрезка времени. Это дает возможность на основе самых общих принципов вывести дифференциальное уравнение рассматриваемого процесса, которое представляет собой наиболее общую связь между существенными для исследуемых процессов величинами.
Связь между величинами, участвующими в передаче теплоты теплопроводностью, устанавливается в этом случае так называемым дифференциальным уравнением теплопроводности, на основе которого строится математическая теория теплопроводности. В основу вывода этого уравнения положен закон сохранения энергии, сочетаемый с законом Фурье.
Закон сохранения энергии может быть сформулирован следующим образом. Выделим в теле некоторую часть объема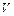 
, ограниченного замкнутой поверхностью 
, через которую происходит тепловое взаимодействие выделенной части с окружающей ее средой. Имеет место следующее утверждение: количество теплоты 
, полученное выделенным объемом за время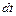 
вследствие теплопроводности, а также от внутренних источников теплоты, равно изменению внутренней энергии вещества, содержащегося в выделенном объеме:
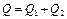, (1.19)
где – изменение внутренней энергии вещества, содержащегося в выделенном объеме 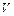за время ; 
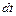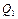– количество теплоты, введенное в выделенный объем путем теплопроводности за время ; 
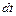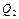– количество теплоты, которое выделилось в объеме 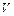за время 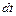вследствие внутренних источников теплоты.
Это утверждение вместе с законом Фурье (1.14) положено в основу вывода дифференциального уравнения теплопроводности. Для облегчения вывода примем следующие допущения:
1. Деформация рассматриваемого объема, связанная с изменением температуры, является очень малой по сравнению с самим объемом, и она не учитывается.
2. Макроскопические частицы тела неподвижны относительно друг друга.
Пусть 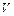– выделенный объем произвольной формы части тела, ограниченный замкнутой поверхностью (не обязательно изотермической);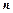 
– единичный вектор внешней нормали к точкам поверхности 
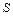(рис. 1.8); 
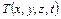– температура тела в точке 
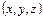в момент времени 
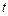. Вычислим общее количество теплоты , полученное выделенным объемом за малый отрезок времени 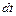, имея в виду, что 
. Для вычисления 
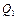воспользуемся законом Фурье в скалярной форме (1.14). Количество теплоты, подведенное в выделенный объем через элементарную площадку 
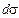за время 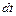, равно (с учетом того, что направление потока теплоты противоположно направлению нормали):
, (1.20)
где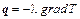 
– вектор плотности теплового потока.
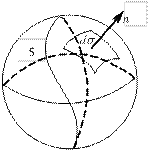
Рис. 1.8 Ограниченная замкнутая поверхность
Количество теплоты, протекающее за время 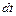через площадь поверхности , выразится интегралом:
, (1.21)
где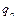 
– проекция вектора 
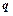на нормаль .
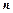Поверхностный интеграл (1.21) можно преобразовать в объемный по формуле Остроградского-Гаусса, связывающей двойной интеграл по поверхности с тройным интегралом по объему 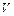, ограниченному этой поверхностью:
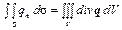. (1.22)
Таким образом,
. (1.23)
Выделение или поглощение теплоты внутри объема 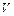удобно характеризовать с помощью плотности (мощности) тепловых источников. Под плотностью тепловых источников понимают такую функцию 
, когда в элементарном объеме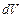 
за отрезок времени 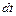выделяется количество теплоты, равное
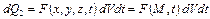. (1.24)
Тогда за отрезок времени 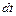в теле объемом 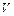выделится количество теплоты
, (1.25)
где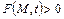 
. Если 
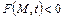, то теплота не выделяется, а поглощается. Функция 
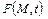считается непрерывной и ограниченной.
Общее количество теплоты , полученное выделенным объемом ,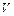
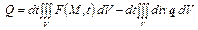. (1.26)
Согласно формуле (2.19) это количество теплоты равно изменению внутренней энергии вещества, содержащегося в выделенном объеме. Указанное изменение на основании первого закона термодинамики может быть выражено формулой:
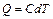, (1.27)
где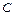 
– теплоемкость выделенного объема; 
– изменение его температуры.
Таким образом, 
может быть вычислено двумя способами. С одной стороны, по формуле (1.26), с другой – путем учета изменения температуры в точках объема 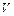, ограниченного поверхностью 
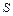. В точке 
за промежуток времени 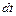температура 
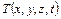изменится на величину:
.
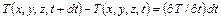Элементу объема 
массой 
для такого изменения температуры потребуется количество теплоты, равное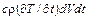 
, а всему объему
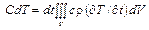, (1.28)
где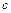 
– удельная теплоемкость, Дж/(кг·К); 
– плотность вещества, кг/м3;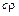 
, Дж/(м3·К).
Принимая во внимание (1.27), с учетом (1.26) и (1.28) находим:
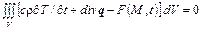. (1.29)
Равенство (1.29) должно выполняться для любой части тела объемом 
. Это возможно только тогда, когда в каждой точке внутри тела
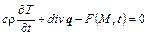. (1.30)
Это заключение справедливо, если левая часть в равенстве (1.30) – непрерывная функция. Предположим, что в точке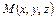 
равенство нарушается, т. е., например, 
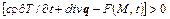. Тогда, интегрируя обе части неравенства по некоторой области 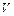, содержащей точку 
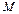, получим противоречие с условием (1.29).
Так как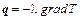 
, то равенство (1.30) можно записать в виде:
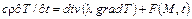. (1.31)
Уравнение (1.31) называется дифференциальным уравнением теплопроводности или уравнением Фурье.
Для изотропного гомогенного тела параметры , ,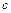 
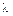постоянные. Так как 
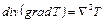, где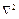 
– оператор Лапласа, то, разделив обе части (1.31) на 
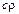, получим:
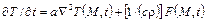, (1.32)
где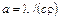 
– коэффициент пропорциональности, называемый температуропроводностью, м2/с.
В декартовых координатах уравнение (1.32) имеет вид:
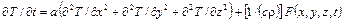. (1.33)
В цилиндрических координатах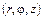 
, связанных с декартовыми координатами соотношениями
,
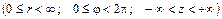
уравнение (1.32) принимает вид:
.
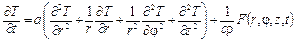В сферических координатах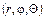 
, связанных с декартовыми координатами соотношениями
,
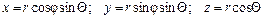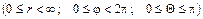
уравнение (1.32) записывается в виде:
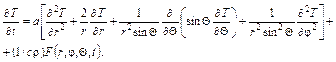
В частном случае, когда температурное поле обладает сферической симметрией, последнее уравнение (при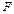 
= 0) принимает вид:
.
Если вместо 
ввести новую функцию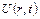 
с помощью подстановки 
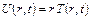, то вместо уравнения относительно после несложных преобразований получим следующее уравнение:
,
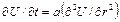аналогичное уравнению теплопроводности для неограниченной пластины (или тонкого стержня с теплоизолированной боковой поверхностью). Применение указанной подстановки позволяет использовать найденные аналитические решения тепловых задач для бесконечной пластины при описании соответствующих температурных полей в сферических телах (сплошной или полый шар).
В отличие от 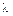, которая характеризует теплопроводящую способность тела, 
характеризует его теплоинерционные свойства и является мерой скорости выравнивания температурного поля в рассматриваемой среде. Действительно, по определению,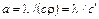 
, где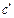 
– объемная изобарная теплоемкость. Отсюда температуропроводность 
прямо пропорциональна теплопроводности 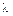и обратно пропорциональна аккумуляционной способности 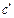вещества. Особенно наглядным становится физический смысл в уравнении теплопроводности, когда отсутствует внутреннее тепловыделение и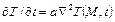 
. Зная вблизи точки 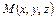зависимость температуры от координат, можно предсказать, как быстро будет изменяться температура в этой точке при переходе к следующему моменту времени. При этом, чем больше (т. е. чем меньше 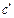), тем пропорционально быстрее меняется во времени температура. Таким образом, 
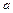характеризует способность вещества изменять с большей или меньшей скоростью свою температуру во времени.
Оператор Лапласа в правой части (1.32) характеризует изменение теплового потока в точке 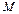и (в геометрическом смысле) является мерой кривизны изотермической поверхности в этой точке. Этим и обусловлено изменение температуры в данной точке, так как наибольшая скорость перестройки температурного поля отвечает участкам большей кривизны и наоборот. Для иллюстрации этих соображений на рис. 1.9 рассмотрим две температурные кривые, соответствующие одномерному температурному полю 
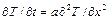(без источников теплоты 
), для момента времени 
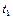(кривая 1) и 
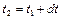(кривая 2). Из рисунка видно, что за время 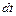температура наиболее изменилась на участках и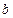 
, где температурная кривая обладает большей кривизной.
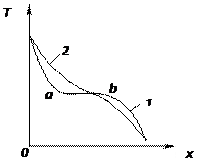
Рис. 1.9 Схема к объяснению скорости изменения температуры
В то же время знак оператора Лапласа в данной точке показывает, в каких случаях температура этой точки при переходе от момента времени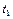 
к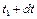 
возрастает (нагревание) и в каких случаях убывает (охлаждение).
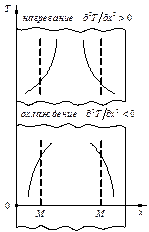
Рис. 1.10 Схема к объяснению влияния оператора Лапласа н
а температурное состояния тела
Возрастание температуры в данной точке обусловливается тем, что в слой материала, охватывающий эту точку, подводится теплоты больше, чем за тот же отрезок времени отводится (величина 
положительна). При убывании температуры, наоборот, отводится теплоты больше, чем за время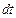 
подводится (величина отрицательна) (рис. 1.10).
Уравнение (1.32) выведено при условии некоторой идеализации процесса и в этом смысле является феноменологическим (описательным) уравнением аналитической теории теплопроводности. Вопрос о том, насколько точно оно описывает реальный физический процесс теплопроводности, может быть решен только сравнением результатов, полученных при решении уравнения, с экспериментальными данными.
Уравнение (1.32) представляет собой дифференциальное уравнение в частных производных, в котором независимыми переменными являются время и три пространственные координаты, а зависимой переменной – функция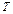 
(температура). Это уравнение первой степени (линейное), поскольку зависимая переменная 
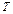входит в него в первой степени. Но вместе с тем, оно является уравнением второго порядка, так как дифференциальный оператор 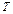содержит производные второго порядка от 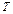по пространственным переменным. Функция 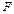считается заданной функцией, в общем случае функцией координат и времени.
Уравнение теплопроводности (1.32) в курсах математической физики относится к дифференциальным уравнениям параболического типа и согласно этому типу уравнений для него выбираются соответствующие аналитические методы решения.
В случае, когда температура рассматриваемого тела в любой его точке не изменяется во времени, т. е. является функцией только координат (установившееся состояние), то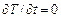 
и уравнение (1.32) принимает вид:
, (1.34)
где плотность тепловых источников 
уже не зависит от времени.
Уравнение (1.34) называется уравнением Пуассона.
Если внутри тела отсутствуют тепловые источники и температурное поле стационарно, то имеем уравнение (в декартовых координатах)
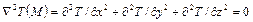, (1.35)
которое называется уравнением Лапласа.
Функции, удовлетворяющие уравнению Лапласа, называются гармоническими. Уравнение Лапласа принадлежит к дифференциальным уравнениям эллиптического типа.
УСЛОВИЯ ОДНОЗНАЧНОСТИ
Дифференциальное уравнение теплопроводности (1.31) является математической моделью целого класса явлений теплопроводности, и при его интегрировании может быть получено бесчисленное множество различных решений. Чтобы из этого множества найти одно частное решение, соответствующее определённой конкретной задаче, необходимо иметь дополнительные данные, не содержащиеся в исходном дифференциальном уравнении. Эти дополнительные условия, которые в совокупности с дифференциальным уравнением однозначно определяют конкретную задачу теплопроводности, называются условиями однозначности.
В условия однозначности входят:
1. Геометрические условия, характеризующие форму и размеры тела, в котором протекает процесс теплообмена. Например, если рассматривается стержень, то, поместив систему координат так, как это показано на рис. 2.1 а, можно математически описать данное тело неравенством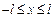 
; форма и размеры тела (рис. 2.1 б) в виде прямоугольника опишутся неравенствами 
, 
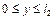; в случае круга радиусом 
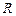или его части (рис. 2.1 в, г), или кругового сектора (рис. 2.1 д) соответственно запишем: 
, 
; 
, 
; 
, .
| |
| |
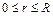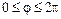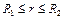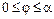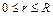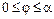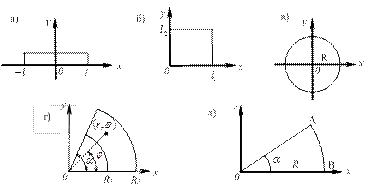
2. Физические условия, характеризующие физические свойства тела (тепло- и температуропроводность), а также закон распределения внутренних источников теплоты.
3. Граничные условия, характеризующие особенности теплового взаимодействия граничной поверхности тела с окружающей средой.
4. Временные или начальные условия, характеризующие температурное состояние тела в исходный (начальный) момент времени.
Перечисленные условия в совокупности определяют одно (конкретное) явление теплопроводности, поэтому они и названы условиями однозначности или условиями единственности.
Для тела определенной геометрической формы с определенными (известными) физическими свойствами условия однозначности сводятся к заданию начального и граничного условий. Эти условия в совокупности называются краевыми условиями – начальное условие является временным краевым условием, а граничное условие – пространственным краевым условием. Дифференциальное уравнение теплопроводности вместе с краевыми условиями составляет краевую задачу теплопроводности. Для установившегося (стационарного) процесса теплопроводности в задании начального условия нет необходимости, и в этом случае краевая задача будет состоять из уравнения теплопроводности и граничных условий.
Дата: 2018-11-18, просмотров: 270.
