ТЕМПЕРАТУРНЫЙ ГРАДИЕНТ
Рассмотрим две бесконечно близкие изотермические поверхности с температурами 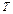 и
и 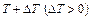 и какую-либо точку
и какую-либо точку 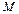 , лежащую на одной из них (рис. 1.4). Перемещаясь из точки
, лежащую на одной из них (рис. 1.4). Перемещаясь из точки 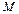 вдоль любых направлений, можно обнаружить, что интенсивность изменения температуры по различным направлениям неодинакова. При перемещении по изотермической поверхности температура не изменяется. Если же перемещаться вдоль какого-либо направления
вдоль любых направлений, можно обнаружить, что интенсивность изменения температуры по различным направлениям неодинакова. При перемещении по изотермической поверхности температура не изменяется. Если же перемещаться вдоль какого-либо направления 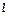 , пересекающего изотермические поверхности, то наблюдается изменение температуры. Используя понятие производной скалярного поля по заданному направлению, можно описать его локальные свойства, т. е. изменение температуры
, пересекающего изотермические поверхности, то наблюдается изменение температуры. Используя понятие производной скалярного поля по заданному направлению, можно описать его локальные свойства, т. е. изменение температуры 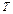 при переходе от точки
при переходе от точки 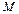 к близкой точке
к близкой точке 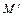 по направлению
по направлению 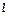 . Скорость изменения температуры
. Скорость изменения температуры 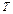 в точке
в точке 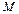 в направлении
в направлении 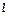 характеризуется производной функции
характеризуется производной функции 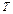 :
:
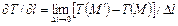 . (1.3)
. (1.3)
Производная функции 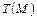 по направлению
по направлению 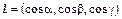 вычисляется по формуле:
вычисляется по формуле:
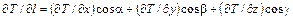 .
.
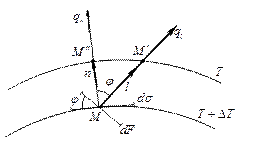
Рис. 1.4 Схема к определению теплового потока
Наибольшая разность температур на единицу длины вектора перемещения 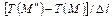 наблюдается в направлении нормали
наблюдается в направлении нормали  к изотермической поверхности (рис. 1.4). В соответствии с (1.3) максимальная скорость изменения температуры при этом равна пределу отношения изменения температуры
к изотермической поверхности (рис. 1.4). В соответствии с (1.3) максимальная скорость изменения температуры при этом равна пределу отношения изменения температуры 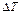 к расстоянию между изотермическими поверхностями по нормали
к расстоянию между изотермическими поверхностями по нормали 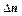 , когда
, когда 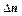 стремится к нулю:
стремится к нулю:
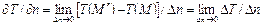 . (1.4)
. (1.4)
Таким образом, в любой точке 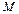 изотермической поверхности можно построить некоторый вектор, направленный по нормали к этой поверхности в сторону увеличения температуры. Абсолютная величина этого вектора равна изменению температуры на единице длины перемещения в рассматриваемом направлении – скорости возрастания температуры (т. е. производной от температурной функции
изотермической поверхности можно построить некоторый вектор, направленный по нормали к этой поверхности в сторону увеличения температуры. Абсолютная величина этого вектора равна изменению температуры на единице длины перемещения в рассматриваемом направлении – скорости возрастания температуры (т. е. производной от температурной функции 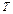 по направлению нормали
по направлению нормали  ). Такой вектор называют градиентом температуры в точке
). Такой вектор называют градиентом температуры в точке 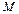 или градиентом температурного поля и записывают в виде символа
или градиентом температурного поля и записывают в виде символа 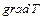 :
:
в декартовых координатах 
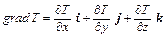 ; (1.5)
; (1.5)
в цилиндрических координатах 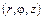
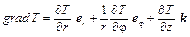 ; (1.6)
; (1.6)
в сферических координатах 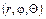
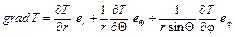 . (1.7)
. (1.7)
Для обозначения вектора (1.5) в теории поля иногда применяют символ 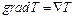 .
.
Согласно сказанному выше, можно записать:
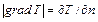 , (1.8)
, (1.8)
т. е. длина вектора 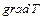 равна скорости возрастания температуры в этом направлении. Здесь и всюду далее
равна скорости возрастания температуры в этом направлении. Здесь и всюду далее  – единичный вектор нормали. Температурный градиент показывает, насколько интенсивно меняется температура тела.
– единичный вектор нормали. Температурный градиент показывает, насколько интенсивно меняется температура тела.
Производная от функции 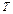 по направлению нормали
по направлению нормали  и вектор
и вектор 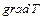 связаны соотношением:
связаны соотношением:
 . (1.9)
. (1.9)
Вектор нормали  к поверхности
к поверхности 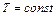 в точке
в точке 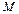 может иметь два противоположных направления, одно из которых можно считать внешним по отношению к данной поверхности, а другое внутренним. Независимо от того, как выбрано направление нормали
может иметь два противоположных направления, одно из которых можно считать внешним по отношению к данной поверхности, а другое внутренним. Независимо от того, как выбрано направление нормали  , вектор (1.5) всегда направлен в сторону возрастания температуры.
, вектор (1.5) всегда направлен в сторону возрастания температуры.
УСЛОВИЯ ОДНОЗНАЧНОСТИ
Дифференциальное уравнение теплопроводности (1.31) является математической моделью целого класса явлений теплопроводности, и при его интегрировании может быть получено бесчисленное множество различных решений. Чтобы из этого множества найти одно частное решение, соответствующее определённой конкретной задаче, необходимо иметь дополнительные данные, не содержащиеся в исходном дифференциальном уравнении. Эти дополнительные условия, которые в совокупности с дифференциальным уравнением однозначно определяют конкретную задачу теплопроводности, называются условиями однозначности.
В условия однозначности входят:
1. Геометрические условия, характеризующие форму и размеры тела, в котором протекает процесс теплообмена. Например, если рассматривается стержень, то, поместив систему координат так, как это показано на рис. 2.1 а, можно математически описать данное тело неравенством 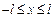 ; форма и размеры тела (рис. 2.1 б) в виде прямоугольника опишутся неравенствами
; форма и размеры тела (рис. 2.1 б) в виде прямоугольника опишутся неравенствами  ,
, 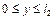 ; в случае круга радиусом
; в случае круга радиусом 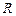 или его части (рис. 2.1 в, г), или кругового сектора (рис. 2.1 д) соответственно запишем:
или его части (рис. 2.1 в, г), или кругового сектора (рис. 2.1 д) соответственно запишем: 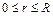 ,
, 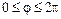 ;
; 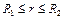 ,
, 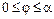 ;
; 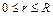 ,
, 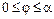 .
.
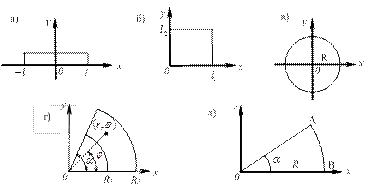
| |
| |
2. Физические условия, характеризующие физические свойства тела (тепло- и температуропроводность), а также закон распределения внутренних источников теплоты.
3. Граничные условия, характеризующие особенности теплового взаимодействия граничной поверхности тела с окружающей средой.
4. Временные или начальные условия, характеризующие температурное состояние тела в исходный (начальный) момент времени.
Перечисленные условия в совокупности определяют одно (конкретное) явление теплопроводности, поэтому они и названы условиями однозначности или условиями единственности.
Для тела определенной геометрической формы с определенными (известными) физическими свойствами условия однозначности сводятся к заданию начального и граничного условий. Эти условия в совокупности называются краевыми условиями – начальное условие является временным краевым условием, а граничное условие – пространственным краевым условием. Дифференциальное уравнение теплопроводности вместе с краевыми условиями составляет краевую задачу теплопроводности. Для установившегося (стационарного) процесса теплопроводности в задании начального условия нет необходимости, и в этом случае краевая задача будет состоять из уравнения теплопроводности и граничных условий.
Метод Л. В. Канторовича
В методе Канторовича задача о нахождении минимума функционала приводится к задаче решения системы не алгебраических, а обыкновенных дифференциальных уравнений при заданных краевых условиях. Поэтому данный метод называется еще методом приведения к обыкновенным дифференциальным уравнениям. Так как полученную таким путем систему дифференциальных уравнений иногда удается решить точно, то считают, что метод Канторовича занимает промежуточное положение между точными аналитическими и прямыми методами.
Основную идею метода Канторовича рассмотрим на примере решения уравнения Пуассона
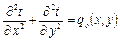 , (4.68)
, (4.68)
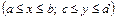
при нулевых граничных условиях на контуре 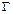
 . (4.69)
. (4.69)
Приближенное решение по методу Канторовича разыскивается в виде:
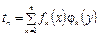 , (4.70)
, (4.70)
где координатные функции 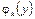 выбираются так, чтобы они удовлетворяли условию (4.69) на прямых
выбираются так, чтобы они удовлетворяли условию (4.69) на прямых 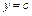 и
и  ;
; 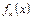 – неизвестные функции.
– неизвестные функции.
Краевой задаче (4.68), (4.69), как уже указывалось выше, соответствует задача об отыскании минимума функционала

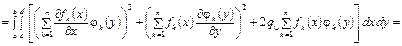
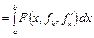 (4.71)
(4.71)
при граничных условиях (4.69), где
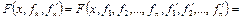
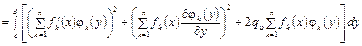 . (4.72)
. (4.72)

Таким образом, задача о минимуме функционала от функции двух переменных сведена к задаче определения минимума функционала от нескольких функций одного переменного.
Как уже указывалось ранее, задача об отыскании минимума функционала типа (4.71), зависящего от нескольких функций одного переменного, в свою очередь сводится к задаче решения системы обыкновенных дифференциальных уравнений Эйлера следующего вида:
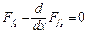 ;
; 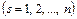 , (4.73)
, (4.73)
где через  обозначено некоторое фиксированное значение
обозначено некоторое фиксированное значение 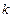 .
.
Или поскольку
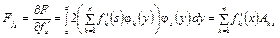 , (4.74)
, (4.74)
где
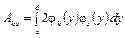 , (4.75)
, (4.75)
то
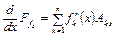 ; (4.76)
; (4.76)
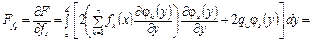
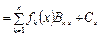 , (4.77)
, (4.77)
где
 , (4.78)
, (4.78)
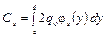 . (4.79)
. (4.79)
Тогда система уравнений (4.73) примет вид:
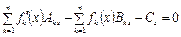 . (4.80)
. (4.80)
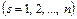
Полученную систему из 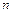 обыкновенных дифференциальных уравнений второго порядка с
обыкновенных дифференциальных уравнений второго порядка с 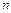 неизвестными
неизвестными 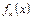 необходимо решить при граничных условиях:
необходимо решить при граничных условиях:
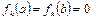 . (4.81)
. (4.81)

В частном случае одного (первого) приближения задача сводится к определению одной функции 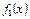 из дифференциального уравнения
из дифференциального уравнения
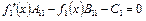 (4.82)
(4.82)
при граничных условиях
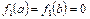 . (4.83)
. (4.83)
В качестве примера на применение метода Канторовича найдем решение краевой задачи для прямоугольника ( 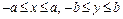 ) в следующей математической постановке:
) в следующей математической постановке:
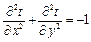 ; (4.84)
; (4.84)
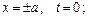 (4.85)
(4.85)
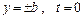 . (4.86)
. (4.86)
Нахождение решения этой задачи равносильно решению задачи о минимуме интеграла
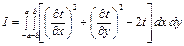 (4.87)
(4.87)
при условиях (4.85), (4.86).
Решение задачи (4.84) – (4.86) в первом приближении принимается в виде:
 . (4.87)
. (4.87)
Соотношение (4.87) удовлетворяет граничному условию (4.86).
Вычисляя коэффициенты в (4.82), получаем:
 ;
;
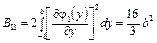 ; (4.88)
; (4.88)
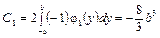 .
.
Уравнение (4.82) при этом примет вид:
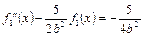 . (4.89)
. (4.89)
Общее решение этого уравнения будет:
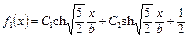 . (4.90)
. (4.90)
Постоянные 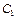 и
и 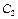 определяются из граничных условий:
определяются из граничных условий:
 . (4.91)
. (4.91)
Поскольку точное решение четная функция, то 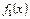 тоже четная функция и
тоже четная функция и  .
.
Тогда используя условие
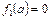 ,
,
получаем
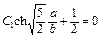 .
.
Откуда
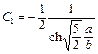 (4.92)
(4.92)
и
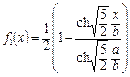 ,
,
а для температурного поля в первом приближении будем иметь
 . (4.93)
. (4.93)
Условие совместности
Упомянутое выше условие 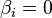 для всех
для всех 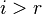 может быть сформулировано в качестве необходимого и достаточного условия совместности:
может быть сформулировано в качестве необходимого и достаточного условия совместности:
Напомним, что рангом совместной системы называется ранг её основной матрицы (либо расширенной, так как они равны).

| Теорема Кронекера — Капелли . Система совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы. Следствия: · Количество главных переменных равно рангу системы и не зависит от её решения. · Если ранг совместной системы равен числу переменных данной системы, то она определена. |
Алгоритм
Блок схема представлена на рисунке. Данный рисунок адаптированный для написания программы на языке С/С++, где a[0] столбец свободных членов.
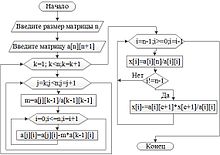
Алгоритм Гаусса для решения САУ
Описание
Алгоритм решения СЛАУ методом Гаусса подразделяется на два этапа.
· На первом этапе осуществляется так называемый прямой ход, когда путём элементарных преобразований над строками систему приводят к ступенчатой или треугольной форме, либо устанавливают, что система несовместна. А именно, среди элементов первого столбца матрицы выбирают ненулевой, перемещают его на крайнее верхнее положение перестановкой строк и вычитают получившуюся после перестановки первую строку из остальных строк, домножив её на величину, равную отношению первого элемента каждой из этих строк к первому элементу первой строки, обнуляя тем самым столбец под ним. После того, как указанные преобразования были совершены, первую строку и первый столбец мысленно вычёркивают и продолжают пока не останется матрица нулевого размера. Если на какой-то из итераций среди элементов первого столбца не нашёлся ненулевой, то переходят к следующему столбцу и проделывают аналогичную операцию.
· На втором этапе осуществляется так называемый обратный ход, суть которого заключается в том, чтобы выразить все получившиеся базисные переменные через небазисные и построить фундаментальную систему решений, либо, если все переменные являются базисными, то выразить в численном виде единственное решение системы линейных уравнений. Эта процедура начинается с последнего уравнения, из которого выражают соответствующую базисную переменную (а она там всего одна) и подставляют в предыдущие уравнения, и так далее, поднимаясь по «ступенькам» наверх. Каждой строчке соответствует ровно одна базисная переменная, поэтому на каждом шаге, кроме последнего (самого верхнего), ситуация в точности повторяет случай последней строки.
Метод Гаусса требует 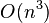 арифметических операций.
арифметических операций.
Этот метод опирается на:

| Теорема (о приведении матриц к ступенчатому виду). Любую матрицу путём элементарных преобразований только над строками можно привести к ступенчатому виду. |
Простейший случай
В простейшем случае алгоритм выглядит так:

· Прямой ход:
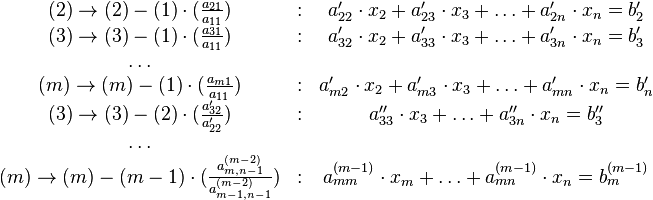
· Обратный ход. Из последнего ненулевого уравнения выражаем базисную переменную через небазисные и подставляем в предыдущие уравнения. Повторяя эту процедуру для всех базисных переменных, получаем фундаментальное решение.
Пример
Покажем, как методом Гаусса можно решить следующую систему:
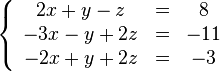
Обнулим коэффициенты при 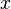 во второй и третьей строчках. Для этого вычтем из них первую строчку, умноженную на
во второй и третьей строчках. Для этого вычтем из них первую строчку, умноженную на 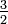 и
и 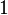 , соответственно:
, соответственно:
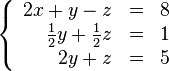
Теперь обнулим коэффициент при 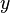 в третьей строке, вычтя из неё вторую строку, умноженную на
в третьей строке, вычтя из неё вторую строку, умноженную на 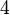 :
:
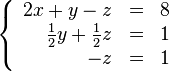
В результате мы привели исходную систему к треугольному виду, тем самым закончим первый этап алгоритма.
На втором этапе разрешим полученные уравнения в обратном порядке. Имеем:
 из третьего;
из третьего;
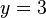 из второго, подставив полученное
из второго, подставив полученное 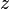
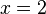 из первого, подставив полученные
из первого, подставив полученные 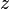 и
и 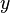 .
.
Таким образом исходная система решена.
В случае, если число уравнений в совместной системе получилось меньше числа неизвестных, то тогда ответ будет записываться в виде фундаментальной системы решений.
Итерационные методы
Итерационные методы устанавливают процедуру уточнения определённого начального приближения к решению. При выполнении условий сходимости они позволяют достичь любой точности просто повторением итераций. Преимущество этих методов в том, что часто они позволяют достичь решения с заранее заданной точностью быстрее, а также позволяют решать большие системы уравнений. Суть этих методов состоит в том, чтобы найти неподвижную точку матричного уравнения
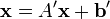 ,
,
эквивалентного начальной системе линейных алгебраических уравнений. При итерации 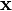 в правой части уравнения заменяется, например, в методе Якоби (метод простой итерации) приближение, найденное на предыдущем шаге:
в правой части уравнения заменяется, например, в методе Якоби (метод простой итерации) приближение, найденное на предыдущем шаге:
 .
.
Итерационные методы делятся на несколько типов, в зависимости от применяемого подхода:
· Основанные на расщеплении: 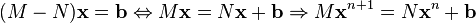
· Вариационного типа: 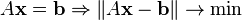
· Проекционного типа: 
Рисунок 2.
Пример 2. Графически отделить корни уравнения (Рисунок 2):
| x lg x = 1. | (4) |
Уравнение (4) удобно переписать в виде равенства:
lg x= 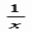 .
.
Отсюда ясно, что корни уравнения (4) могут быть найдены как абсциссы точек пересечения логарифмической кривой y = lg x и гиперболы y =  . Построив эти кривые, приближенно найдем единственный корень
. Построив эти кривые, приближенно найдем единственный корень 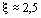 уравнения (4) или определим его содержащий отрезок [2, 3].
уравнения (4) или определим его содержащий отрезок [2, 3].
Итерационный процесс состоит в последовательном уточнении начального приближения х0. Каждый такой шаг называется итерацией. В результате итераций находится последовательность приближенных значений корня х1, х2, ..., хn. Если эти значения с увеличением числа итераций n приближаются к истинному значению корня, то говорят, что итерационный процесс сходится.
Метод половинного деления
Для нахождения корня уравнения (1), принадлежащего отрезку [a, b], делим этот отрезок пополам. Если f  = 0 , то x =
= 0 , то x = 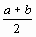 является корнем уравнения. Если f
является корнем уравнения. Если f  не равно 0 (что, практически, наиболее вероятно), то выбираем ту из половин
не равно 0 (что, практически, наиболее вероятно), то выбираем ту из половин 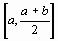 или
или 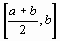 , на концах которой функция f(x) имеет противоположные знаки. Новый суженный отрезок [ а1, b1] снова делим пополам и производим те же самые действия.
, на концах которой функция f(x) имеет противоположные знаки. Новый суженный отрезок [ а1, b1] снова делим пополам и производим те же самые действия.
Метод половинного деления практически удобно применять для грубого нахождения корня данного уравнения, метод прост и надежен, всегда сходится.
Пример 3. Методом половинного деления уточнить корень уравнения
f(x) = x4 + 2 x3 - x - 1 = 0
лежащий на отрезке [ 0, 1] .
Последовательно имеем:
f(0) = - 1; f(1) = 1; f(0,5) = 0,06 + 0,25 - 0,5 - 1 = - 1,19;
f(0,75) = 0,32 + 0,84 - 0,75 - 1 = - 0,59;
f(0,875) = 0,59 + 1,34 - 0,88 - 1 = + 0,05;
f(0,8125) = 0,436 + 1,072 - 0,812 - 1 = - 0,304;
f(0,8438) = 0,507 + 1,202 - 0,844 - 1 = - 0,135;
f(0,8594) = 0,546 + 1,270 - 0,859 - 1 = - 0,043 и т. д.
Можно принять
x = 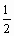 (0,859 + 0,875) = 0,867
(0,859 + 0,875) = 0,867
Метод хорд
В данном методе процесс итераций состоит в том, что в качестве приближений к корню уравнения (1) принимаются значения х1, х2, ..., хn точек пересечения хорды АВ с осью абсцисс (Рисунок 3). Сначала запишем уравнение хорды AB:
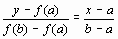 .
.
Для точки пересечения хорды AB с осью абсцисс (х = х1, y = 0) получим уравнение:
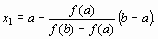
Пусть для определенности f'' (x) > 0 при а 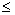 х
х 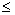 b (случай f'' (x) < 0 сводится к нашему, если записать уравнение в виде - f(x) = 0). Тогда кривая у = f(x) будет выпукла вниз и, следовательно, расположена ниже своей хорды АВ. Возможны два случая: 1) f(а) > 0 (Рисунок 3, а) и 2)f(b) < 0 (Рисунок 3, б).
b (случай f'' (x) < 0 сводится к нашему, если записать уравнение в виде - f(x) = 0). Тогда кривая у = f(x) будет выпукла вниз и, следовательно, расположена ниже своей хорды АВ. Возможны два случая: 1) f(а) > 0 (Рисунок 3, а) и 2)f(b) < 0 (Рисунок 3, б).
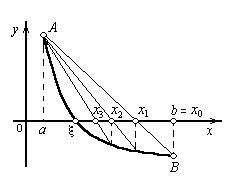
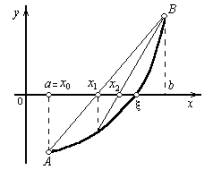
Рисунок 3, а, б.
В первом случае конец а неподвижен и последовательные приближения: x0 = b;
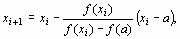 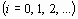
| (5) |
образуют ограниченную монотонно убывающую последовательность, причем
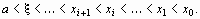
Во втором случае неподвижен конец b, а последовательные приближения: x0 = а;

| (6) |
образуют ограниченную монотонно возрастающую последовательность, причем
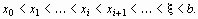
Обобщая эти результаты, заключаем:
1. неподвижен тот конец, для которого знак функции f (х) совпадает со знаком ее второй производной f'' (х);
2. последовательные приближения xn лежат по ту сторону корня x , где функция f (х) имеет знак, противоположный знаку ее второй производной f'' (х).
Итерационный процесс продолжается до тех пор, пока не будет обнаружено, что
| xi - xi - 1|< e ,
где e - заданная предельная абсолютная погрешность.
Пример 4. Найти положительный корень уравнения
f(x) = x3 - 0,2 x2 - 0,2 х - 1,2 = 0
с точностью e = 0,01.
Прежде всего, отделяем корень. Так как
f (1) = -0,6 < 0 и f (2) = 5,6 > 0,
то искомый корень x лежит в интервале [1, 2]. Полученный интервал велик, поэтому разделим его пополам. Так как
f (1,5) = 1,425 > 0, то 1< x < 1,5.
Так как f'' (x) = 6 x - 0,4 > 0 при 1 < х < 1,5 и f (1,5) > 0, то воспользуемся формулой (5) для решения поставленной задачи:
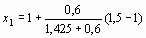 = 1,15;
= 1,15;
|x1 - x0| = 0,15 > e ,
следовательно, продолжаем вычисления;
f (х1) = -0,173;
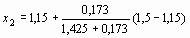 = 1,190;
= 1,190;
|x2 - x1| = 0,04 > e ,
f (х2) = -0,036;
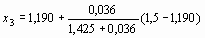 = 1,198;
= 1,198;
|x3 - x2| = 0,008 < e .
Таким образом, можно принять x = 1,198 с точностью e = 0,01.
Заметим, что точный корень уравнения x = 1,2.
Лекция 3
ТЕМПЕРАТУРНЫЙ ГРАДИЕНТ
Рассмотрим две бесконечно близкие изотермические поверхности с температурами 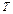 и
и 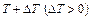 и какую-либо точку
и какую-либо точку 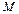 , лежащую на одной из них (рис. 1.4). Перемещаясь из точки
, лежащую на одной из них (рис. 1.4). Перемещаясь из точки 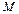 вдоль любых направлений, можно обнаружить, что интенсивность изменения температуры по различным направлениям неодинакова. При перемещении по изотермической поверхности температура не изменяется. Если же перемещаться вдоль какого-либо направления
вдоль любых направлений, можно обнаружить, что интенсивность изменения температуры по различным направлениям неодинакова. При перемещении по изотермической поверхности температура не изменяется. Если же перемещаться вдоль какого-либо направления 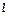 , пересекающего изотермические поверхности, то наблюдается изменение температуры. Используя понятие производной скалярного поля по заданному направлению, можно описать его локальные свойства, т. е. изменение температуры
, пересекающего изотермические поверхности, то наблюдается изменение температуры. Используя понятие производной скалярного поля по заданному направлению, можно описать его локальные свойства, т. е. изменение температуры 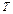 при переходе от точки
при переходе от точки 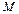 к близкой точке
к близкой точке 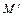 по направлению
по направлению 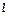 . Скорость изменения температуры
. Скорость изменения температуры 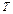 в точке
в точке 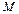 в направлении
в направлении 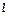 характеризуется производной функции
характеризуется производной функции 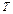 :
:
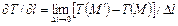 . (1.3)
. (1.3)
Производная функции 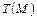 по направлению
по направлению 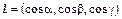 вычисляется по формуле:
вычисляется по формуле:
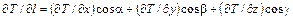 .
.

Рис. 1.4 Схема к определению теплового потока
Наибольшая разность температур на единицу длины вектора перемещения 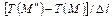 наблюдается в направлении нормали
наблюдается в направлении нормали  к изотермической поверхности (рис. 1.4). В соответствии с (1.3) максимальная скорость изменения температуры при этом равна пределу отношения изменения температуры
к изотермической поверхности (рис. 1.4). В соответствии с (1.3) максимальная скорость изменения температуры при этом равна пределу отношения изменения температуры 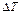 к расстоянию между изотермическими поверхностями по нормали
к расстоянию между изотермическими поверхностями по нормали 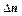 , когда
, когда 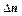 стремится к нулю:
стремится к нулю:
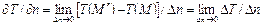 . (1.4)
. (1.4)
Таким образом, в любой точке 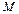 изотермической поверхности можно построить некоторый вектор, направленный по нормали к этой поверхности в сторону увеличения температуры. Абсолютная величина этого вектора равна изменению температуры на единице длины перемещения в рассматриваемом направлении – скорости возрастания температуры (т. е. производной от температурной функции
изотермической поверхности можно построить некоторый вектор, направленный по нормали к этой поверхности в сторону увеличения температуры. Абсолютная величина этого вектора равна изменению температуры на единице длины перемещения в рассматриваемом направлении – скорости возрастания температуры (т. е. производной от температурной функции 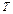 по направлению нормали
по направлению нормали  ). Такой вектор называют градиентом температуры в точке
). Такой вектор называют градиентом температуры в точке 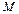 или градиентом температурного поля и записывают в виде символа
или градиентом температурного поля и записывают в виде символа 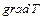 :
:
в декартовых координатах 
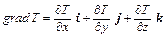 ; (1.5)
; (1.5)
в цилиндрических координатах 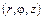
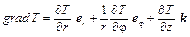 ; (1.6)
; (1.6)
в сферических координатах 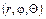
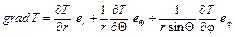 . (1.7)
. (1.7)
Для обозначения вектора (1.5) в теории поля иногда применяют символ 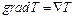 .
.
Согласно сказанному выше, можно записать:
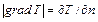 , (1.8)
, (1.8)
т. е. длина вектора 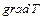 равна скорости возрастания температуры в этом направлении. Здесь и всюду далее
равна скорости возрастания температуры в этом направлении. Здесь и всюду далее  – единичный вектор нормали. Температурный градиент показывает, насколько интенсивно меняется температура тела.
– единичный вектор нормали. Температурный градиент показывает, насколько интенсивно меняется температура тела.
Производная от функции 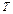 по направлению нормали
по направлению нормали  и вектор
и вектор 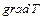 связаны соотношением:
связаны соотношением:
 . (1.9)
. (1.9)
Вектор нормали  к поверхности
к поверхности 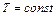 в точке
в точке 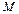 может иметь два противоположных направления, одно из которых можно считать внешним по отношению к данной поверхности, а другое внутренним. Независимо от того, как выбрано направление нормали
может иметь два противоположных направления, одно из которых можно считать внешним по отношению к данной поверхности, а другое внутренним. Независимо от того, как выбрано направление нормали  , вектор (1.5) всегда направлен в сторону возрастания температуры.
, вектор (1.5) всегда направлен в сторону возрастания температуры.
ТЕПЛОВОЙ ПОТОК. ВЕКТОРНАЯ И СКАЛЯРНАЯ ФОРМЫ ЗАКОНА ФУРЬЕ
В теле, не находящемся в полном тепловом равновесии (т. е. обладающим неравномерным распределением температуры), всегда происходит перенос теплоты. Отсюда следует, что для передачи теплоты теплопроводностью необходимо неравенство нулю температурного градиента. В этом смысле температурный градиент является основным физическим параметром, определяющим условие возникновения теплового процесса. Следовательно, соотношение 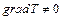 является необходимым условием возникновения внутри тела теплового потока. Тепловой поток в отличие от температуры (величины скалярной) имеет вполне определенное направление, а именно: от точек тела с более высокой к точкам с более низкой температурой. Таким образом, тепловой поток можно рассматривать как вектор, направленный в сторону уменьшения температуры, а поле тепловых потоков – векторным. Для математического описания поля тепловых потоков вводится вектор
является необходимым условием возникновения внутри тела теплового потока. Тепловой поток в отличие от температуры (величины скалярной) имеет вполне определенное направление, а именно: от точек тела с более высокой к точкам с более низкой температурой. Таким образом, тепловой поток можно рассматривать как вектор, направленный в сторону уменьшения температуры, а поле тепловых потоков – векторным. Для математического описания поля тепловых потоков вводится вектор 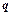 , называемый вектором плотности теплового потока. Под вектором плотности теплового потока в точке
, называемый вектором плотности теплового потока. Под вектором плотности теплового потока в точке 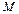 температурного поля понимается вектор, направление которого совпадает с направлением переноса теплоты. Абсолютная величина этого вектора выражает тепловой поток, измеряемый количеством теплоты, проходящей в единицу времени через единицу площади поверхности, перпендикулярной направлению потока в рассматриваемой точке. Обозначим через
температурного поля понимается вектор, направление которого совпадает с направлением переноса теплоты. Абсолютная величина этого вектора выражает тепловой поток, измеряемый количеством теплоты, проходящей в единицу времени через единицу площади поверхности, перпендикулярной направлению потока в рассматриваемой точке. Обозначим через 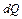 количество теплоты, проходящее через изотермическую поверхность площади
количество теплоты, проходящее через изотермическую поверхность площади 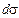 за время
за время 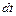 . Тогда абсолютное значение вектора плотности теплового потока можно записать в виде:
. Тогда абсолютное значение вектора плотности теплового потока можно записать в виде:
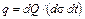 . (1.10)
. (1.10)
Формула (1.10) характеризует плотность теплового потока единичного элемента изотермической поверхности. Понятие плотности теплового потока, как будет показано ниже, применимо к любой, а не только к изотермической, поверхности.
Опыт показывает, что передача теплоты теплопроводностью происходит по нормали к изотермической поверхности от участков тела с большей к участкам с меньшей температурой. Следовательно, вектор плотности теплового потока направлен по нормали к изотермической поверхности в направлении уменьшения температуры. Можно говорить о плотности теплового потока и вдоль любого другого направления 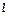 , отличного от направления нормали
, отличного от направления нормали  . В этом случае плотность теплового потока в направлении
. В этом случае плотность теплового потока в направлении 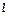 есть проекция вектора
есть проекция вектора 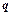 на это направление, т. е. величина
на это направление, т. е. величина 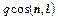 .
.
Идея о существовании органической связи между вектором плотности теплового потока и температурным градиентом легла в основу учения, созданного Фурье. Сущность гипотезы Фурье состоит в том, что тепловой поток через элемент изотермической поверхности вполне определяется значением температурного градиента в рассматриваемой точке 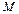 . Действительный смысл этой связи заключается в том, что тепловые потоки в среде всегда
. Действительный смысл этой связи заключается в том, что тепловые потоки в среде всегда
определенно направлены. Возникновение тепловых потоков вдоль изотермических поверхностей невозможно, так как по всей изотермической поверхности составляющая градиента температуры равна нулю. Следовательно, векто-
ры плотности теплового потока 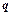 и
и 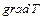 направлены по нормали к изотермической поверхности, но в противоположные стороны (рис. 1.5).
направлены по нормали к изотермической поверхности, но в противоположные стороны (рис. 1.5).
С увеличением перепада температур, т. е. с возрастанием температурного градиента, увеличивается и плотность теплового потока. Опыты показали, что плотность теплового потока можно считать пропорциональной первой степени удельного перепада температуры. Это и явилось основой гипотезы Фурье о наличии простейшей количественной зависимости между абсолютными значениями векторов плотности теплового потока и температурного градиента. На основе этих данных, а также соображений о противоположном направлении этих векторов, закон Фурье в векторном виде записывается следующим образом:
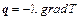 . (1.11)
. (1.11)
Этот закон, сформулированный в виде гипотезы, был подтвержден многочисленными опытами. Выражение (1.11) используется при выводе уравнений, описывающих механизм процесса теплопроводности.
Наглядное представление о мгновенном распределении потоков теплоты могут дать линии, касательные к которым в каждой точке температурного поля совпадают с соответствующими нормалями к изотермическим поверхностям. Такие линии называются линиями теплового потока (рис. 1.5).
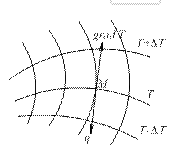
Рис. 1.5 Направление векторов плотности теплового потока и градиента температуры
Коэффициент пропорциональности 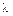 называется теплопроводностью и является физической константой, характеризующей теплопроводящие свойства материала данного тела. Подставляя в уравнение (1.11) единицы
называется теплопроводностью и является физической константой, характеризующей теплопроводящие свойства материала данного тела. Подставляя в уравнение (1.11) единицы 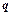 и температурного градиента, найдем для
и температурного градиента, найдем для 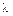 единицу измерения Вт/ (м К).
единицу измерения Вт/ (м К).
Числовое значение теплопроводности определяет количество теплоты, проходящее через единицу площади изотермической поверхности в единицу времени при градиенте температуры, равном единице. Подобно другим величинам этого ряда (удельная теплоемкость, электрическое сопротивление, модуль упругости и т. п.) значение теплопроводности в общем случае зависит от природы вещества, его структуры, влажности, давления, температуры и других факторов. В большинстве случаев теплопроводность 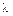 для различных материалов определяется опытным путем. С повышением температуры
для различных материалов определяется опытным путем. С повышением температуры 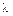 возрастает, а от давления она практически не зависит.
возрастает, а от давления она практически не зависит.
Зависимость теплопроводности от температуры в общем случае довольно сложная, однако для большинства твердых тел, жидкостей и газов при умеренных температурах она оказывается почти линейной, т. е. 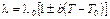 , где
, где 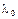 – теплопроводность при температуре
– теплопроводность при температуре 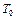 ; b – постоянная, определяемая опытным путем. В классической аналитической теории теплопроводности величина
; b – постоянная, определяемая опытным путем. В классической аналитической теории теплопроводности величина 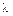 для упрощения выводов считается постоянной (т. е.
для упрощения выводов считается постоянной (т. е. 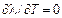 ).
).
Соотношение (1.10) запишем в виде:
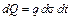 . (1.12)
. (1.12)
Как отмечалось выше, нормаль  к элементу
к элементу 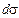 изотермической поверхности может иметь два направления (направляющие косинусы этих направлений отличаются только знаками). Условимся считать тепловой поток положительным, если его направление совпадает с выбранным направлением нормали, и отрицательным, если оно ему противоположно. Для абсолютных значений векторов, входящих в равенство (1.11), следует, что
изотермической поверхности может иметь два направления (направляющие косинусы этих направлений отличаются только знаками). Условимся считать тепловой поток положительным, если его направление совпадает с выбранным направлением нормали, и отрицательным, если оно ему противоположно. Для абсолютных значений векторов, входящих в равенство (1.11), следует, что 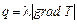 . Теперь в равенстве (1.8) необходимо поставить знак минус, т. е.
. Теперь в равенстве (1.8) необходимо поставить знак минус, т. е. 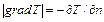 и
и
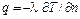 . (1.13)
. (1.13)
Действительно, для нормали, совпадающей с направлением градиента, имеем 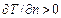 ; перенос же теплоты происходит всегда в направлении уменьшения температуры, т. е. в противоположную сторону и, следовательно, должно быть
; перенос же теплоты происходит всегда в направлении уменьшения температуры, т. е. в противоположную сторону и, следовательно, должно быть 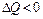 , или, что то же самое,
, или, что то же самое, 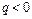 , что и объясняет знак минус в формуле (1.13). Изменив направление нормали на противоположное, имеем
, что и объясняет знак минус в формуле (1.13). Изменив направление нормали на противоположное, имеем 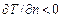 , но тогда
, но тогда 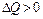 и, следовательно, знак минус сохраняется. Подставляя теперь в (1.12) вместо
и, следовательно, знак минус сохраняется. Подставляя теперь в (1.12) вместо  правую часть равенства (1.13), можно записать закон Фурье в скалярной форме:
правую часть равенства (1.13), можно записать закон Фурье в скалярной форме:
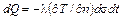 . (1.14)
. (1.14)
Выражение (1.14) определяет количество теплоты, проходящее через элементарный участок 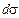 изотермической поверхности за время
изотермической поверхности за время 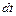 по направлению нормали к площадке (рис. 1.6). Количество теплоты, прошедшее за время
по направлению нормали к площадке (рис. 1.6). Количество теплоты, прошедшее за время 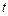 через изотермическую поверхность конечных размеров площадью
через изотермическую поверхность конечных размеров площадью 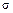 будет определяться по соотношению:
будет определяться по соотношению:
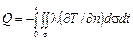 .
.
Тепловой поток может быть определен вдоль любого направления через площадь, перпендикулярную этому направлению. Однако на практике часто встречаются случаи, когда площадка ориентирована в поле произвольным образом. Покажем, что равенство (1.14) справедливо для любых поверхностей, а не только для изотермических.
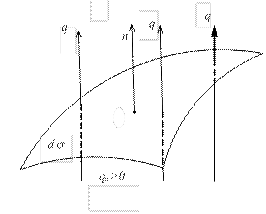
Рис. 1.6 Изотермическая поверхность
Выберем произвольную элементарную площадку 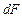 так, чтобы угол между нормалью
так, чтобы угол между нормалью 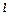 к ней и вектором плотности теплового потока
к ней и вектором плотности теплового потока 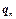 в рассматриваемой точке был равен
в рассматриваемой точке был равен 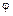 (рис. 1.7). Поток теплоты по нормали
(рис. 1.7). Поток теплоты по нормали 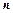 в направлении
в направлении 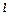 можно вычислить, используя соотношения (1.10) и (1.14):
можно вычислить, используя соотношения (1.10) и (1.14):

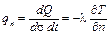 ;
;
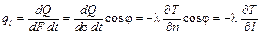 ,
,
так как 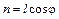 .
.
Отсюда находим, что
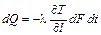 . (1.16)
. (1.16)
Общее количество теплоты, протекающее за время 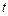 через конечную площадь поверхности
через конечную площадь поверхности 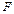 :
:
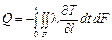 . (1.17)
. (1.17)
В частном случае, когда тепловой режим стационарный и температурный градиент одинаков по всей площади поверхности 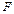 , можно записать:
, можно записать:
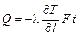 .
.

Рис. 1.7 Схема к определению теплового потока
Таким образом, для определения количества теплоты, проходящей через какую-либо площадь поверхности твердого тела, нужно знать температурное поле внутри данного тела, что составляет главную задачу аналитической теории теплопроводности.
Так как 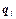 является составляющей вектора плотности теплового потока
является составляющей вектора плотности теплового потока 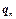 , т. е.
, т. е. 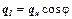 , то из этого уравнения следует, что самым большим тепловым потоком, отнесенным к единице площади поверхности, будет тот, который рассчитан вдоль нормали
, то из этого уравнения следует, что самым большим тепловым потоком, отнесенным к единице площади поверхности, будет тот, который рассчитан вдоль нормали 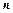 к изотермической поверхности
к изотермической поверхности 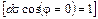 .
.
В этом параграфе не рассматриваются усложненные анизотропией случаи теплопроводности. Для таких веществ как древесина, слюда и т. п., теплопроводность 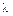 зависит от направления, поэтому простое правило косинусов для получения составляющей
зависит от направления, поэтому простое правило косинусов для получения составляющей 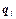 несправедливо.
несправедливо.
Если спроектировать вектор плотности теплового потока на координатные оси, то в соответствии с его определением (1.11) можно записать:
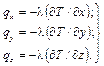 (1.18)
(1.18)
Тепловые потоки, выраженные соотношениями (1.18), являются составляющими вектора плотности теплового потока.
Дата: 2018-11-18, просмотров: 912.