Тема 1.2. Точный аналитический метод – метод разделения переменных (метод Фурье)            

Тема 1.3. Применение метода Фурье

Тема 1.4. Метод Л.В.Канторовича.

Метод Л. В. Канторовича

В методе Канторовича задача о нахождении минимума функционала приводится к задаче решения системы не алгебраических, а обыкновенных дифференциальных уравнений при заданных краевых условиях. Поэтому данный метод называется еще методом приведения к обыкновенным дифференциальным уравнениям. Так как полученную таким путем систему дифференциальных уравнений иногда удается решить точно, то считают, что метод Канторовича занимает промежуточное положение между точными аналитическими и прямыми методами.

Основную идею метода Канторовича рассмотрим на примере решения уравнения Пуассона

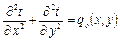,                                    (4.68)

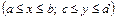
при нулевых граничных условиях на контуре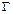

.                                             (4.69)

Приближенное решение по методу Канторовича разыскивается в виде:

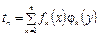,                                 (4.70)

где координатные функции 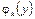 выбираются так, чтобы они удовлетворяли условию (4.69) на прямых  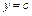и ;  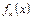– неизвестные функции.

Краевой задаче (4.68), (4.69), как уже указывалось выше, соответствует задача об отыскании минимума функционала

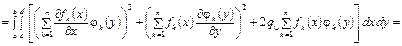
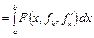                                        (4.71)

при граничных условиях (4.69), где

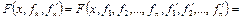
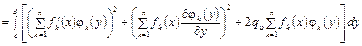. (4.72)

Таким образом, задача о минимуме функционала от функции двух переменных сведена к задаче определения минимума функционала от нескольких функций одного переменного.

Как уже указывалось ранее, задача об отыскании минимума функционала типа (4.71), зависящего от нескольких функций одного переменного, в свою очередь сводится к задаче решения системы обыкновенных дифференциальных уравнений Эйлера следующего вида:

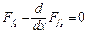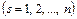; ,                       (4.73)

где через  обозначено некоторое фиксированное значение .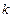

Или поскольку

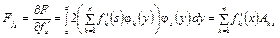,         (4.74)

где

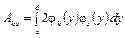,                                 (4.75)

то

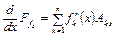;                                (4.76)

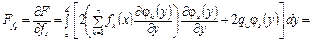
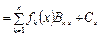,                                  (4.77)

где

,                         (4.78)

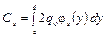.                                 (4.79)

Тогда система уравнений (4.73) примет вид:

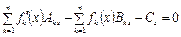.                   (4.80)

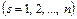
Полученную систему из 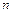 обыкновенных дифференциальных уравнений второго порядка с  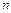неизвестными  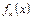необходимо решить при граничных условиях:

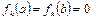.                                     (4.81)

В частном случае одного (первого) приближения задача сводится к определению одной функции 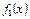 из дифференциального уравнения

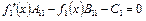                             (4.82)

при граничных условиях

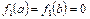.                                     (4.83)

В качестве примера на применение метода Канторовича найдем решение краевой задачи для прямоугольника ( 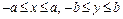) в следующей математической постановке:

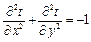;                                    (4.84)

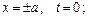                                    (4.85)

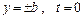.                                     (4.86)

Нахождение решения этой задачи равносильно решению задачи о минимуме интеграла

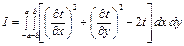                      (4.87)

при условиях (4.85), (4.86).

Решение задачи (4.84) – (4.86) в первом приближении принимается в виде:

.                       (4.87)

Соотношение (4.87) удовлетворяет граничному условию (4.86).

Вычисляя коэффициенты в (4.82), получаем:

;

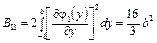;                         (4.88)

.

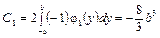Уравнение (4.82) при этом примет вид:

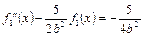.                              (4.89)

Общее решение этого уравнения будет:

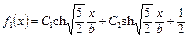.                       (4.90)

Постоянные 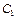 и 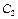 определяются из граничных условий:

.                                     (4.91)

Поскольку точное решение четная функция, то 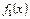 тоже четная функция и .

Тогда используя условие

,

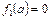получаем

.

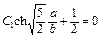Откуда

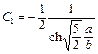                                      (4.92)

и

,

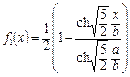а для температурного поля в первом приближении будем иметь

.                            (4.93)