При любом а, при котором выражение 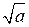 имеет смысл, справедливо равенство
имеет смысл, справедливо равенство 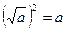 .
.
3. Воспользуйтесь определением арифметического квадратного корня из числа а.
Арифметическим квадратным корнем из числа а называют неотрицательное число 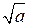 , квадрат которого равен а:
, квадрат которого равен а: 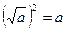 .
.
4. Возведите предложенные числа в квадрат и сравните полученные числа. Воспользуйтесь тем, что большему значению аргумента х функции  соответствует большее значение функции. Например,
соответствует большее значение функции. Например,  , так как 3,7 > 1,9.
, так как 3,7 > 1,9.
5. Внесите множители под знак корня и воспользуйтесь тем, что большему значению аргумента х функции 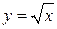 соответствует большее значение функции. Например,
соответствует большее значение функции. Например,  , или
, или  , так как 4×3 < 9×2, или 12 < 18.
, так как 4×3 < 9×2, или 12 < 18.
Преобразование вида 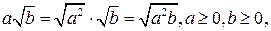 называют внесением множителя под знак корня.
называют внесением множителя под знак корня.
6. Вначале выполните действия в скобках. Вынесите множитель из-под знака арифметического корня, выполните сокращение. Потом возведите полученное выражение в указанную степень. Степень корня находится по определению степени. Например,  При необходимости воспользуйтесь правилами возведения произведения или частного в степень.
При необходимости воспользуйтесь правилами возведения произведения или частного в степень.
Преобразование вида  называют вынесением множителя из-под знака корня.
называют вынесением множителя из-под знака корня.
7. Вначале выполните действия в скобках. При необходимости разложите выражение в знаменателе на множители. Воспользуйтесь формулами сокращенного умножения.
При сложении (вычитании) дробей с разными знаменателями нужно привести их к общему знаменателю, а затем воспользоваться правилом сложения (вычитания) дробей с одинаковыми знаменателями:  .
.
Квадрат суммы двух выражений равен квадрату первого выражения, плюс удвоенное произведение первого и второго выражений, плюс квадрат второго выражения: ( a + b )2 = a 2 + 2 ab + b 2 ; a 2 + 2 ab + b 2 = ( a + b )2.
Квадрат разности двух выражений равен квадрату первого выражения, минус удвоенное произведение первого и второго выражений, плюс квадрат второго выражения: ( a – b )2 = a 2 – 2 ab + b 2 ; a 2 – 2 ab + b 2 = ( a – b )2.
Произведение разности двух выражений и их суммы равно разности квадратов этих выражений: ( a – b )( a + b ) = a 2 – b 2 .
Разность квадратов двух выражений равно произведению разности этих выражений на их сумму: a 2 – b 2 = ( a – b )( a + b ).
8. Функция 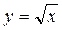 имеет смысл при х ³ 0. Для выполнения задания нужно составить и решить соответствующее неравенство.
имеет смысл при х ³ 0. Для выполнения задания нужно составить и решить соответствующее неравенство.
9. Для выполнения задания нужно решить уравнение, считая переменную, которую нужно выразить через остальные, неизвестной, а остальные — известными. Преобразуйте так это уравнение, чтобы член с неизвестной стоял в левой части, а остальные члены — в правой. Приведите вначале выражение, стоящее в правой части, к общему знаменателю. Останется записать выражение, обратное полученному.
10. Воспользуйтесь теоремой Виета.
Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.
Для квадратного уравнения ах2 + bx + c = 0, имеющего корни х1 и х2, имеем:
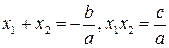 .
.
Зная произведение корней и один из корней, несложно найти второй. Проверьте, равна ли сумма корней  .
.
11. Воспользуйтесь определением неравенства.
Число а больше числа b , если разность а – b — положительное число; число а меньше числа b , если разность а – b — отрицательное число.
Установите знак выражения, которое представляет разность данных чисел..
12. Обратная пропорциональность задается формулой  . Коэффициент k определяется из условия, что график этой функции проходит через точку, заданную непосредственно или определяемую по графику. Для нахождения k нужно подставить координаты этой точки в заданную формулу и из полученного уравнения найти k.
. Коэффициент k определяется из условия, что график этой функции проходит через точку, заданную непосредственно или определяемую по графику. Для нахождения k нужно подставить координаты этой точки в заданную формулу и из полученного уравнения найти k.
13. Вы знакомы с графиками линейной функции, а также с графиками функций 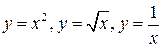 . Выберите искомый график из представленных графиков. Кроме того, можно, при необходимости воспользоваться следующими утверждениями.
. Выберите искомый график из представленных графиков. Кроме того, можно, при необходимости воспользоваться следующими утверждениями.
Областью определения функции у = х2 является вся числовая прямая.
Областью определения функции у =  является промежуток [0; + ¥ ).
является промежуток [0; + ¥ ).
Областью определения функции у = 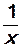 является множество (- ¥ ; 0) È (0; + ¥ ).
является множество (- ¥ ; 0) È (0; + ¥ ).
График функции y = - f ( x ) получается из графика функции y = f ( x ) симметричным отображением относительно оси х.
14. На оси ординат найдите область, удовлетворяющую неравенству, приведенному в условии для заданной переменной, затем отметьте соответствующую часть графика и, наконец, на оси абсцисс зафиксируйте тот участок, который соответствует этой части графика.
15. Воспользуйтесь определением концентрации раствора.
Концентрацией раствора k называют выраженное в процентах отношение объёма (массы) «чистого» вещества v к объёму (массе) всего раствора V :
 .
.
Вначале найдите количество «чистого» вещества в каждом растворе, воспользовавшись соотношением  , затем общее количество «чистого» вещества в смеси и, наконец, искомую концентрацию «чистого» вещества в смеси.
, затем общее количество «чистого» вещества в смеси и, наконец, искомую концентрацию «чистого» вещества в смеси.
16. Воспользуйтесь следующими утверждениями.
Расстояние от точки до оси х равно модулю ординаты этой точки.
Расстояние от точки до оси у равно модулю абсциссы этой точки.
Расстояние от точки с известными координатами до начала координат находится по теореме Пифагора.
Сравните модули соответствующих координат точек, приведенных в ответе, с модулем этой же координаты данной точки.
17. Воспользуйтесь подобием треугольников.
Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
Отношение соответственных сторон подобных треугольников называют коэффициентом подобия .
Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
18. Проведите в заданном многоугольнике высоту. В полученном прямоугольном треугольнике найдите один из катетов. Искомый катет вычислите по теореме Пифагора.
В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
19. Выделите прямоугольный треугольник со сторонами, упомянутыми в условии, или равными им. Найдите острые углы этого треугольника, затем воспользуйтесь соотношениями между сторонами и углами треугольника.
В треугольнике против большей стороны лежит больший угол.
В треугольнике против большего угла лежит большая сторона.
Сумма острых углов прямоугольного треугольника равна 90 ° .
20. Воспользуйтесь признаками или определениями параллелограмма, прямоугольника, ромба, определением и свойствами средней линии треугольника.
Если диагонали четырёхугольника точкой пересечения делятся пополам, то этот четырёхугольник — параллелограмм.
Если диагонали параллелограмма равны, то этот параллелограмм является прямоугольником.
Ромбом называют параллелограмм, у которого все стороны равны.
Средней линией треугольника называют отрезок, соединяющий середины двух его сторон.
Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
Вначале докажите, что искомый четырёхугольник является параллелограммом, а затем попытайтесь применить признак прямоугольника или ромба.
21. Можно выделить прямоугольный треугольник и воспользоваться свойством катета, лежащего против угла 30°, и теоремой Пифагора. А можно выделить равносторонний треугольник и при необходимости воспользоваться теоремой Пифагора.
В прямоугольном треугольнике с углом 30 ° катет, лежащий против этого угла, равен половине гипотенузы.
В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
Равнобедренный треугольник, в котором имеется угол 60 ° , является равносторонним.
22. Не пропустите при подсчёте «большие» многоугольники, объединяющие два меньших.
23. Воспользовавшись свойствами средней линии трапеции и теоремой Фалеса, докажите, что отрезки средней линии трапеции являются средними линиями некоторых треугольников. Затем воспользуйтесь свойствами средней линии треугольника.
Средняя линия трапеции параллельна основаниям и равна их полусумме.
Параллельные прямые, пересекающие стороны угла и отсекающие на одной из них равные отрезки, отсекают равные отрезки и на другой стороне.
Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
24. Воспользуйтесь формулами площадей параллелограмма, треугольника, трапеции.
Площадь параллелограмма равна произведению его стороны и высоты, проведенной на эту сторону.
Площадь треугольника равна половине произведению его стороны и высоты, проведенной на эту сторону.
Площадь трапеции равна половине произведения суммы её оснований и высоты.
Обратите внимание на то, что у треугольника и четырёхугольника равные высоты.
25. Воспользуйтесь формулой площади трапеции.
Площадь трапеции равна половине произведения суммы её оснований и высоты:  , где S — площадь трапеции, a и b — её основания, h — высота.
, где S — площадь трапеции, a и b — её основания, h — высота.
Продвинутый уровень Вариант 1
1. О натуральных числах p и q известно, что p < q. Расположите в порядке возрастания числа a = 1, 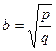 ,
,  .
.
А . b < c < a. Б . b < a < c. В . a < b < c. Г . a < c < b.
2. Упростите выражение 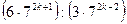 , где k — натуральное число.
, где k — натуральное число.
А. 343. Б. 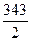 . В. 14. Г. 686.
. В. 14. Г. 686.
3. Сравните числа 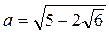 и
и 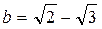 .
.
А. a = b. Б. a > b. В. a < b. Г. Сравнить нельзя.
4. Чему равно выражение  ?
?
А. –2 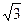 Б. 2
Б. 2 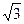 . В. 4. Г. –4.
. В. 4. Г. –4.
5. Укажите наибольшее целое число х, при котором справедливо равенство |x – 2| = 2 – x.
А. Не существует. Б. –2. В. 2. Г. 0.
6. Уравнение x2 + px + q = 0 имеет 2 корня. Сколько корней будет иметь уравнение, полученное из данного уменьшением его свободного члена?
А. 2. Б. 1. В. 0. Г. Однозначного ответа нет.
7. Квадратное уравнение ax2 – bx – 1 = 0 будет иметь корень, равный –1, если …
А . а – b = 1. Б . а + b = 1. В . – a + b = 1. Г . a = b = 0.
8. Укажите все значения p, при которых квадратный трехчлен – x2 + 3x + p имеет корни разных знаков.
А. р > 0. Б. р < 0. В. р ³ – 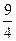 . Г. p £
. Г. p £ 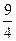 .
.
9. Сколько существует точек на графике функции y= 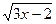 , у которых абсцисса и ордината совпадают?
, у которых абсцисса и ордината совпадают?
А. Ни одной. Б. Одна. В. Две. Г. Три.
10. Какую прямую из приведенных в ответах пересекает график функции  ?
?
 А. x = 0. Б. x =
А. x = 0. Б. x = 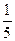 . В. y =2,5. Г. Среди приведенных такой прямой нет.
. В. y =2,5. Г. Среди приведенных такой прямой нет.
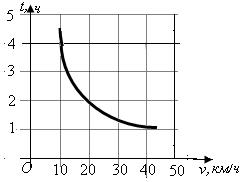
11. На рисунке дан график зависимости времени t, затрачиваемого на путь из пункта А в пункт В, от скорости движения v, представляющей собой обратную пропорциональность. Каково расстояние между пунктами А и В?
А. 40 км. Б. 20 км. В. 10 км. Г. 25 км.
12. Цена продукта потребления увеличилась на 20%. Было решено не увеличивать затрат на покупку этого продукта. На сколько процентов придется уменьшить потребление данного продукта?
А. На 20%. Б. На 25%. В. На 16 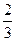 %. Г. На 26
%. Г. На 26  % .
% .
13. В треугольнике АВС через точку О пересечения биссектрис углов В и С проведена прямая, параллельная ВС и пересекающая АВ в точке М. Треугольник ВОМ является …
А. прямоугольным. Б. тупоугольным. В. равнобедренным. Г. равносторонним.
14.  В параллелограмме АВС D биссектрисы углов В и D пересекают диагональ АС в точках M и N. Четырехугольник В N DМ является …
В параллелограмме АВС D биссектрисы углов В и D пересекают диагональ АС в точках M и N. Четырехугольник В N DМ является …
А. трапецией. Б. параллелограммом.
В. ромбом. Г. прямоугольником.
15. В равнобедренном треугольнике боковые стороны равны по 6 дм. Из произвольно взятой точки основания проведены две прямые, параллельные боковым сторонам треугольника. Периметр получившегося параллелограмма равен …
А. 18 дм. Б. 12 дм. В. 15 дм. Г. величине отличной от приведенных.
16. Диагональ квадрата равна d. Его сторона равна …
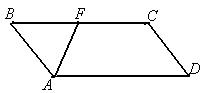 А.
А.  . Б.
. Б.  . В.
. В. 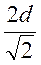 . Г.
. Г.  .
.
17. Биссектриса угла А в параллелограмме АВС D делит сторону ВС на отрезки 7 см и 14 см. (считая от вершины В). Периметр параллелограмма равен …
А. 56 см. Б. 42 см. В. 28 см. Г. 70 см.
18. Дан треугольник АВС, площадь которого S, О — точка пересечения медиан С K и ВF (KÎAB, FÎАС). Площадь треугольника ВОС равна…
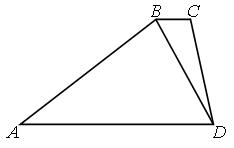 А.
А.  . Б.
. Б.  . В.
. В. 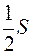 . Г.
. Г. 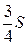 .
.
19. Если АВСD — трапеция с основаниями AD и ВС, ÐABD = ÐBCD, AD = 9, BC = 1, то диагональ BD равна …
А. 3. Б. 4. В. 6. Г. 8.
20. Совокупность точек плоскости, удаленных от двух пересекающихся прямых на одно и то же расстояние, образует …
А. прямую. Б. две прямые. В. полосу. Г. окружность.
Продвинутый уровень. Вариант 2.
1. О натуральных числах m и n известно, что m > n . Расположите в порядке возрастания числа a = 1, 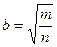 ,
, 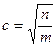 .
.
А . с < b < a. Б . a < b < c. В . с < a < b. Г . а < c < b.
2. Упростите выражение 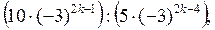 где k — натуральное число.
где k — натуральное число.
А. 54. Б. –54. В. –18. Г. 18.
3. Сравните числа 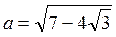 и
и 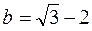 .
.
А. а > b. Б. а = b. В. a < b. Г. Сравнить нельзя.
4. Чему равно выражение 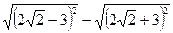 ?
?
А. –6. Б. 6. В. 4 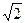 . Г. – 4
. Г. – 4 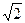 .
.
5. Укажите наименьшее целое число x, при котором справедливо равенство
|–x – 1| = 1 + x.
А. 1. Б. –1. В. 0. Г. Такого числа не существует.
6. Уравнение x2 + px + q = 0 не имеет корней. Сколько корней будет иметь уравнение, полученное из данного увеличением его свободного члена?
А. Одно. Б. Два. В. Ни одного. Г. Однозначного ответа нет.
7. Квадратное уравнение x2 – bx – с = 0 имеет корень, равный –1, если …
А. b – c = –1. Б. b – c = 1. В. b = – c. Г. b – c = 0.
8. Укажите все значения a, при которых квадратный трехчлен ax2 + 2x + 3 имеет корни разных знаков.
А. a £ 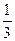 . Б. а >
. Б. а > 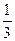 . В. a > 0. Г. a < 0.
. В. a > 0. Г. a < 0.
9. Сколько существует точек на графике функции y = 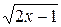 , у которых абсцисса и ордината совпадают?
, у которых абсцисса и ордината совпадают?
А. Ни одной. Б. Одна. В. Две. Г. Три.
10. Какую прямую из приведенных в ответах пересекает график функции 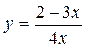 ?
?
А. x = 0. Б. y = – 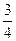 . В. x =
. В. x = 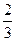 . Г. Среди приведенных такой прямой нет
. Г. Среди приведенных такой прямой нет
11. 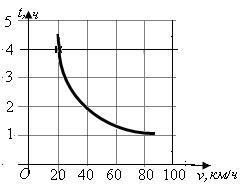 На рисунке дан график зависимости времени t, затрачиваемого на путь из пункта А в пункт В, от скорости движения v, представляющей собой обратную пропорциональную зависимость. Каково расстояние между пунктами А и В?
На рисунке дан график зависимости времени t, затрачиваемого на путь из пункта А в пункт В, от скорости движения v, представляющей собой обратную пропорциональную зависимость. Каково расстояние между пунктами А и В?
А. 40 км. Б. 60 км. В. 100 км. Г. 80 км.
12. В бассейн проведена труба. Вследствие засорения её приток воды уменьшился на 60%. На сколько процентов вследствие этого увеличится время, необходимое для заполнения бассейна?
А. На 150%. Б. На 50%. В. На 250%. Г. На 60%.
13. Какой вид имеет треугольник, отсекаемый биссектрисой острого угла равнобедренной трапеции, если боковая сторона меньше меньшего основания трапеции?
А. Прямоугольный. Б. Остроугольный. В. Равнобедренный. Г. Разносторонний.
14. Биссектрисы углов параллелограмма пересекают его стороны в точках M , N , P и Q. Четырехугольник MNPQ является …
А. трапецией. Б. прямоугольником. В. параллелограммом. Г. ромбом.
15. 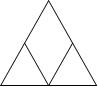 В равнобедренный треугольник вписан параллелограмм так, что угол параллелограмма совпадает с углом при вершине треугольника, а вершина противоположного угла лежит на основании. Боковая сторона треугольника равна 8 см. Периметр параллелограмма равен …
В равнобедренный треугольник вписан параллелограмм так, что угол параллелограмма совпадает с углом при вершине треугольника, а вершина противоположного угла лежит на основании. Боковая сторона треугольника равна 8 см. Периметр параллелограмма равен …
А.16 см. Б.24 см. В.12 см. Г.8 см.
16. 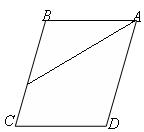 Гипотенуза равнобедренного прямоугольного треугольника равна с. Его катет равен …
Гипотенуза равнобедренного прямоугольного треугольника равна с. Его катет равен …
А. 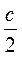 . Б.
. Б. 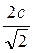 . В.
. В. 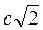 . Г.
. Г. 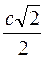 .
.
17. Биссектриса угла А в параллелограмме АВС D делит сторону ВС на отрезки 7 см и 14 см (считая от вершины С). Периметр параллелограмма равен …
А. 56 см. Б. 70 см. В. 42 см. Г. 35 см.
18. 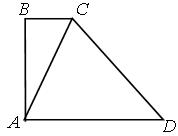 Дан треугольник АВС, площадь которого S, О — точка пересечения медиан А K и ВD (KÎBС, DÎАС). Площадь треугольника АОD равна…
Дан треугольник АВС, площадь которого S, О — точка пересечения медиан А K и ВD (KÎBС, DÎАС). Площадь треугольника АОD равна…
А. 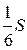 . Б.
. Б. 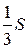 . В.
. В. 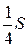 . Г.
. Г. 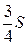 .
.
19. Если АВСD — трапеция (АD||ВС), ÐBАС = ÐCDА, BC = 2, АD = 8, то диагональ АС равна …
А. 5. Б. 4. В. 3. Г. 6.
20. Совокупность точек плоскости, удаленных от двух параллельных прямых на одно и то же расстояние, образует …
А. прямую. Б. две прямые. В. полосу. Г. окружность.
Продвинутый уровень. Вариант 3.
1. О натуральных числах a и b известно, что a < b. Расположите в порядке убывания числа x = 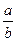 , y =
, y = 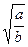 , z =
, z = 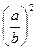 .
.
А . z > y > x. Б . y > z > x. В . z > x > y. Г . y > x > z.
2. Упростите выражение 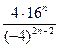 .
.
А. 64. Б. –64. В. 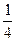 . Г. –
. Г. – 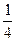 .
.
3. Сравните числа 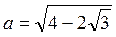 и
и 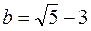 .
.
А. a = b. Б. a < b. В. a > b. Г. Сравнить нельзя.
4. Чему равно выражение 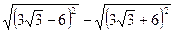 ?
?
А. –12. Б. 12. В. 6 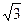 . Г. –6
. Г. –6 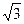 .
.
5. Укажите наибольшее целое число х, при котором справедливо равенство
|x + 1| = –1 – x.
А. Не существует. Б. –1. В. 1. Г. 0.
6. Уравнение x2 + px + q = 0 имеет 2 корня. Сколько корней будет иметь уравнение, полученное из данного увеличением его свободного члена?
А. 0. Б. 1. В. 2. Г. Однозначного ответа нет.
7. Квадратное уравнение а x2 – x – с = 0 имеет корень, равный –2, если …
А. 4а – c = –2. Б. 4а – c = 2. В. 4а = – c + 2. Г. 4а – c = 0.
8. Укажите все значения b и с, при которых квадратный трехчлен 2x2 + bx + c имеет противоположные корни.
А. b = 0, c > 0. Б. b = 0, c < 0. В. c < 0, b — любое. Г. b ¹ 0, c — любое.
9. Сколько общих точек имеют графики функций 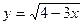 и y = - x?
и y = - x?
А. 3. Б. 2. В. 1. Г. 0.
10. График функции y= 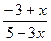 не имеет общих точек с прямой …
не имеет общих точек с прямой …
 А. x = 3. Б. y =
А. x = 3. Б. y = 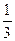 . В. x =
. В. x = 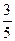 . Г. у = –
. Г. у = – 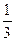 .
.
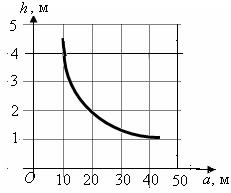
11. На рисунке дан график зависимости между стороной а и высотой h параллелограмма постоянной площади (S = ah). Площадь параллелограмма равна …
А. 10 м2. Б. 20 м2. В. 30 м2. Г. 40 м2.
12. Благодаря внедрению рационализаторского предложения время, необходимое для изготовления некоторой детали, уменьшилось на 20%. На сколько процентов увеличилась производительность труда?
А. На 25%. Б. На 20%. В. На 125%. Г. На 75%.
13. Какой вид имеет треугольник, отсекаемый биссектрисой угла параллелограмма, равного 120°?
А. Прямоугольный. Б. Тупоугольный.
В. Равносторонний. Г. Разносторонний.
14. 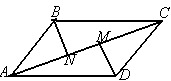 В параллелограмме АВС D перпендикуляры, проведенные через вершины тупых углов к диагонали АС, пересекают ее в точках М и N. Четырехугольник BND М является …
В параллелограмме АВС D перпендикуляры, проведенные через вершины тупых углов к диагонали АС, пересекают ее в точках М и N. Четырехугольник BND М является …
А. параллелограммом. Б. прямоугольником.
 В. ромбом. Г. трапецией.
В. ромбом. Г. трапецией.
15. В равнобедренный прямоугольный треугольник вписан прямоугольник так, что один угол у них общий. Катет треугольника равен 8 см. Периметр прямоугольника равен …
А. 8 см. Б. 12 см. В. 24 см. Г. 16 см.
16. Сторона равностороннего треугольника равна а. Его высота равна …
А. 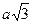 . Б.
. Б. 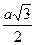 . В.
. В. 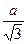 . Г.
. Г. 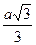 .
.
17. Биссектриса угла прямоугольника делит сторону пополам, а периметр его равен 60 см. Вычислите стороны прямоугольника.
А. По 15 см. Б. 10 и 20 см. В. 12 и 18 см. Г. 6 и 24 см.
18. Дан треугольник АВС, площадь которого равна S, О — точка пересечения медиан АD и ВЕ (DÎВС, ЕÎАС). Найдите площадь четырехугольника ODCE.
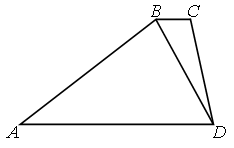 А.
А. 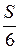 . Б.
. Б. 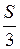 . В.
. В. 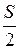 . Г.
. Г. 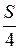 .
.
19. Если АВСD — трапеция с основаниями AD и ВС, ÐBАD = ÐBDС, AD = 16, BC = 4, то диагональ BD равна …
А. 5. Б. 6. В. 7. Г. 8.
20. Совокупность точек плоскости, удаленных от двух точек на одно и то же расстояние, образует…
А. окружность. Б. прямую. В. две прямые. Г. полосу.
Подсказки к заданиям продвинутого уровня
1. Воспользуйтесь следующими свойствами функций у = 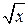 и у = х2.
и у = х2.
Если 0 < x < 1, то 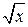 > x ; если х > 1, то
> x ; если х > 1, то 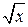 < x .
< x .
Если 0 < x < 1, то x 2 < x ; если х > 1, то x 2 > x .
Сравните данные дроби с 1, а затем примените приведенные свойства.
2. Примените правила действий над одночленами и степенями с одинаковыми основаниями.
3. Установите знаки а и b. Помните, что знаком 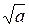 обозначают арифметическое значение корня.
обозначают арифметическое значение корня.
4. Воспользуйтесь следующим утверждением.
При любом значении а верно равенство 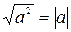 .
.
Установите знаки выражений, стоящих в скобках.
5. Воспользуйтесь следующими утверждениями.
Модуль положительного числа равен этому числу;
Дата: 2018-11-18, просмотров: 910.