Центр математического просвещения
Я.С. Бродский, А.Л. Павлов
ПОВТОРИМ МАТЕМАТИКУ
8 – 9 классы

Донецк 2018
ББК 22.1я 72
Б88
Бродский Я.С., Павлов А.Л. Повторим математику. Пособие для дополнительного обучения математике учащихся 8-9 классов, 2018, с.54.
Настоящее пособие предназначено для повторения математики при подготовке к её изучению в 9-м классе.
В пособии содержатся задания пяти уровней: базового, основного, продвинутого, повышенного и углубленного. Тесты базового, основного и продвинутого уровней предназначены для диагностики уровня математической подготовки учащихся общеобразовательных школ. Тесты повышенного и углубленного уровня можно использовать для более глубокой дифференциации уровня подготовки учащихся. Они могут быть использованы для подготовки к школьным и районным олимпиадам и другим соревнованиям, предусматривающим высокий уровень математической подготовки.
Пособие состоит из двух частей. В первой части представлен материал для обучения. В этой части содержатся примерно равноценные варианты тестов каждого из уровней, указания к выполнению заданий каждого уровня, а также ответы. Вторая часть пособия содержит систему заданий для проверки владения учащимися действиями и приёмами, представленными в первой части.
Пособие адресовано учащимся 8-9 классов. Оно может быть использовано учителями математики для диагностики математической подготовки учащихся.
Дорогой друг!
Настоящее пособие позволит тебе:
- выяснить прочность и глубину усвоения математики, изученной ранее школе;
- повторить материал и систематизировать свои знания по математике;
- подготовиться к дальнейшему обучению математике и её применениям.
Пособие состоит из тренажёра и контрольного задания. Тренажёр предназначен для выявления пробелов в математической подготовке и их устранения. Контрольное задание предназначено для оценивания успешности повторения математики.
Задания для тренировки имеют пять уровней: базовый, основной, продвинутый, повышенный и углубленный. Это позволит тебе двигаться, как по ступенькам: сначала почувствовать, что твёрдо стоишь на первой ступеньке — хорошо владеешь базовым уровнем, — затем поднимаешься на вторую и так можно добраться до верхней ступеньки — углублённого уровня. Если же ты почувствуешь, что подъём для тебя на какую-то следующую ступеньку пока не под силу, остановись, подготовься к дальнейшему подъёму.
Хорошо потренировавшись хотя бы на первых двух уровнях, можно начинать выполнять контрольное задание, продолжая тренировки. Контрольное задание состоит из двух частей: основного и дополнительного заданий.
Задания для тренировки и контроля представлены в тестовой форме. Возможно, у тебя уже есть опыт работы с такими заданиями. Если нет, то ты его приобретёшь. Все необходимые разъяснения для выполнения заданий приведены далее.
Надеемся, что работа над пособием будет полезной и интересной.
Желаем успехов!
Повторенье – мать учения
Повторим математику
Как организовать повторение
Организация повторения состоит из организации тренировок и организации работы над контрольным заданием.
Организация тренировок
1. Надо сначала попробовать выполнить самостоятельно задания первого варианта теста базового уровня, содержащегося в тренажёре. Выбранные ответы записывайте на отдельном листочке.
Базовый уровень Вариант 1
1. Вычислите: 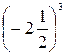 .
.
А. 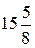 . Б. –
. Б. – 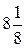 . В.
. В. 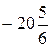 . Г.
. Г. 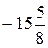 .
.
2. Вычислите значение выражения 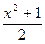 при
при 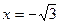 .
.
А. –1. Б. 2. В. 1. Г. –2.
3. Вычислите значение выражения 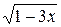 при х = –5.
при х = –5.
А. ±4. Б. 16. В. 4. Г. ±16.
4. Между какими последовательными натуральными числами заключено число 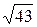 ?
?
А. 6 и 7. Б. 5 и 6. В. 7 и 8. Г. 4 и 5.
5. Сравните числа 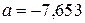 и b = – 7,563.
и b = – 7,563.
А . a = b. Б . a < b. В . a > b. Г . Сравнить нельзя.
6. Упростите выражение 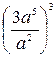 .
.
А. 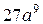 . Б.
. Б. 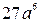 . В.
. В. 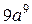 . Г.
. Г. 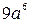 .
.
7. Упростите выражение 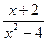 .
.
А. х – 2. Б. 2 – х. В. 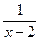 . Г.
. Г. 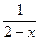 .
.
8. Укажите все значения х, при которых имеет смысл выражение 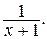
А. 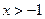 . Б.
. Б. 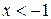 . В.
. В. 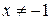 . Г.
. Г. 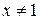 .
.
9. Из формулы 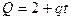 выразите переменную t.
выразите переменную t.
А. 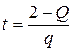 . Б.
. Б. 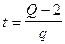 . В.
. В. 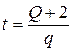 . Г.
. Г. 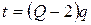 .
.
10. Корнями уравнения (х + 5)x = 0 являются числа …
А. 0 и –5. Б. 0 и 5. В. 1 и –5. Г. 1 и 5.
11. Сравните числа а и b, если а – b = 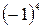 .
.
А . а < b. Б . a = b. В . a > b. Г . 
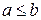 .
.
12. График функции y = 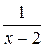 проходит через точку ¼
проходит через точку ¼
А. (1; 1). Б. 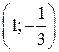 . В.
. В. 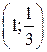 . Г. (1; –1).
. Г. (1; –1).
13. 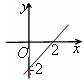 На рисунке изображен график функции …
На рисунке изображен график функции …
А . y = x + 2. Б . y = –x + 2. В . y = x – 2. Г . y = –x – 2.
14. 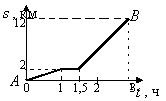 На рисунке представлен график прямолинейного движения туриста из пункта А в пункт В, где s — расстояние туриста до пункта А, t — время движения. Сколько времени двигался турист до привала?
На рисунке представлен график прямолинейного движения туриста из пункта А в пункт В, где s — расстояние туриста до пункта А, t — время движения. Сколько времени двигался турист до привала?
А. 2 ч. Б. 3 ч. В. 1,5 ч. Г. 1 ч.
15. В классе 10 % учащихся занимаются только легкой атлетикой, 50 % — только гимнастикой, а остальные 12 учеников —только игровыми видами спорта. Сколько учащихся в классе?
А. 35. Б. 30. В. 25. Г. 28.
16. Какая из точек E(–1; 2), F(2; –1), G(2; –3), H(4; 6) расположена ближе всего к оси х?
А. F. Б. E. В. G. Г. H.
17. Через точку А(–1; 4) проведена прямая, параллельная оси у. Точка ее пересечения с осью х имеет координаты …
А. (0; 4). Б. (4; 0). В. (0; –1). Г. (–1; 0).
18. Из одной точки, лежащей вне прямой, проведены к этой прямой перпендикуляр длиной 6 см и наклонная длиной 10 см. Длина ее проекции на прямую равняется …
А. 4 см. Б. 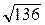 см. В. 8 см. Г. величине, отличной от приведенных.
см. В. 8 см. Г. величине, отличной от приведенных.
19. В прямоугольном треугольнике АВС длины катетов АС и ВС равны соответственно 5 см и 7 см. Сравните острые углы А и В.
А. ÐA < ÐB. Б. ÐA = ÐB. В. ÐA > ÐB. Г. Сравнить нельзя.
20. Углы параллелограмма могут равняться ...
А. 35° и 145°. Б. 50° и 40°. В. 120° и 150°. Г. 75° и 115°.
21. В прямоугольном треугольнике один из углов равняется 60°, а катет, прилежащий к нему, равен 12 см. Гипотенуза равна ....
А. 12 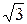 см . Б. 18 см. В. 18
см . Б. 18 см. В. 18 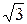 см. Г. 24 см.
см. Г. 24 см.
22. Сколько диагоналей можно провести из одной вершины шестиугольника?
А. 6. Б. 5. В. 4. Г. 3.
23. Из точки, лежащей вне круга, проведены к окружности, ограничивающей этот круг, две взаимно перпендикулярные касательные. Радиус круга равен 10 см. Длина каждой касательной равна …
А. 10 см. Б. 5 см. В. 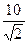 см. Г. величине, отличной от приведенных.
см. Г. величине, отличной от приведенных.
24. Как изменится площадь прямоугольника, если одну сторону увеличить вдвое, а другую — уменьшить вдвое?
А. Увеличится в 2 раза. Б. Уменьшится в 2 раза.
В. Увеличится в 1,5 раза. Г. Не изменится.
25. В круге проведена хорда длиной 8 см, удаленная от центра на 3 см. Диаметр круга равен ...
А. 5 см. Б. 12 см. В. 10 см. Г. величине, отличной от приведенных.
Базовый уровень Вариант 2
1. Вычислите: 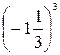 .
.
А. 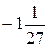 . Б.
. Б. 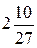 . В.
. В. 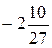 . Г.
. Г. 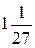 .
.
2. Вычислите значение выражения 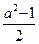 при
при 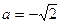 .
.
А. 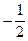 . Б.
. Б. 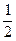 . В.
. В. 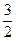 . Г.
. Г. 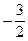 .
.
3. Вычислите значение выражения 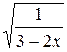 при х = –11.
при х = –11.
А. ± 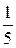 . Б.
. Б. 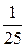 . В. ±
. В. ± 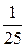 . Г.
. Г. 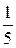 .
.
4. Между какими последовательными натуральными числами расположено число 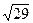 ?
?
А. 5 и 6. Б. 6 и 7. В. 4 и 5. Г. 7 и 8.
5. Сравните числа 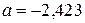 и
и 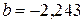 .
.
А . a = b. Б . a < b. В . a > b. Г . Сравнить нельзя.
6. Упростите выражение 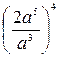 .
.
А. 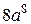 . Б.
. Б. 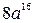 . В.
. В. 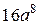 . Г.
. Г. 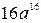 .
.
7. Упростите выражение 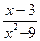 .
.
А. 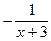 . Б.
. Б. 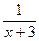 . В.
. В. 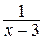 . Г.
. Г. 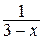 .
.
8. Укажите все значения х, при которых имеет смысл выражение 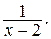
А. 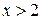 . Б.
. Б. 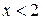 . В.
. В. 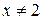 . Г.
. Г. 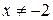 .
.
9. Из формулы 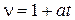 выразите переменную
выразите переменную 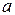 .
.
А. 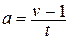 . Б.
. Б. 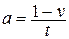 . В.
. В. 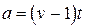 . Г.
. Г. 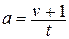 .
.
10. Найдите корни уравнения 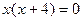 .
.
А. 0 и 4. Б. 1 и 4. В. 0 и – 4. Г. 1 и – 4.
11. Сравните числа а и b, если а – b = (–1)5 .
А . а > b. Б . a = b. В . a ³ b. Г . b > a.
12. График функции y = 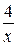 проходит через точку…
проходит через точку…
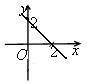 А. (–2; 2). Б. (–2; –2). В.
А. (–2; 2). Б. (–2; –2). В. 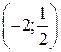 . Г.
. Г. 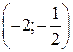 .
.
13. На рисунке изображен график функции …
А. 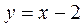 . Б.
. Б. 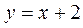 . В. .
. В. . 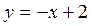 . Г.
. Г. 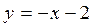 .
.
14. 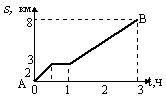 На рисунке представлен график движения туриста из пункта А в пункт В, где s — расстояние от туриста до пункта А, t — время движения. Сколько километров прошел турист после привала?
На рисунке представлен график движения туриста из пункта А в пункт В, где s — расстояние от туриста до пункта А, t — время движения. Сколько километров прошел турист после привала?
А. 5 км. Б. 4 км. В. 3 км. Г. 8 км.
15. В классе 20 % учащихся изучают только английский язык, 30 % — только французский, а остальные 15 учащихся — только немецкий. Сколько учащихся в классе?
А. 25. Б. 24. В. 35. Г. 30.
16. Какая из точек М(2; –1), N(–1; 2), P(0; 3), Q(1; –4) расположена дальше всех от оси у?
А. Q. Б. M. В. P. Г. N.
17. Через точку А(2; –3) проведена прямая, параллельная оси х. Точка ее пересечения с осью у имеет координаты …
А. (0; –3). Б. (2; 0). В. (0; 2). Г. (–3; 0).
18. Из одной точки, расположенной вне прямой, проведены к этой прямой перпендикуляр длиной 8 см и наклонная, проекция которой на прямую равна 6 см. Длина наклонной равна …
А. 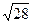 см. Б. 9 см. В. 10 см. Г. величине, отличной от приведенных.
см. Б. 9 см. В. 10 см. Г. величине, отличной от приведенных.
19. В прямоугольном треугольнике АВС угол А равен 40°. Сравните катеты АС и ВС.
А. A С < B C. Б. A C = B C. В. A C > B C. Г. Сравнить нельзя.
20. Углы равнобедренной трапеции могут быть равны ...
А. 35° и 155°. Б. 50° и 40°. В. 120° и 150°. Г. 75° и 105°.
21. В прямоугольном треугольнике один из углов равен 60°, а гипотенуза — 20 см. Чему равен меньший катет?
А. 10 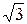 см . Б. 8
см . Б. 8 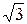 см. В. 10 см. Г. 8 см.
см. В. 10 см. Г. 8 см.
22. Сколько диагоналей можно провести из одной вершины пятиугольника?
А. 3. Б. 2. В. 4. Г. 1.
23. Из точки, лежащей вне круга, проведены к окружности, ограничивающей этот круг, две взаимно перпендикулярные касательные, длиной 8 см каждая. Радиус круга равен …
А. 4 см. Б. 8 см. В. 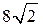 см. Г. величине, отличной от приведенных.
см. Г. величине, отличной от приведенных.
24. Как изменится площадь равнобедренного треугольника, если ее основание уменьшить в 3 раза, а высоту увеличить вдвое?
А. Уменьшится в 6 раз. Б. Увеличится в 2 раза.
В. Увеличится в 3 раза. Г. Уменьшится в 1,5 раза.
25. В круге диаметром 26 см проведена хорда, удаленная от центра на 5 см. Длина хорды равна ...
А. 12 см. Б. 18 см. В. 24 см. Г. величине, отличной от приведенных.
Базовый уровень. Вариант 3.
1. Вычислите: 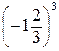 .
.
А. 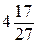 . Б.
. Б. 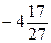 . В. -
. В. - 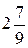 . Г.
. Г. 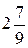 .
.
2. Вычислите значение выражения 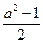 при
при 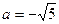 .
.
А. –1. Б. 2. В. 1. Г. –2.
3. Вычислите значение выражения 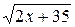 при х = –5.
при х = –5.
А. ±5. Б. 25. В. 5. Г. ±25.
4. Между какими двумя последовательными натуральными числами находится число 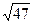 ?
?
А. 6 и 7. Б. 5 и 6. В. 7 и 8. Г. 4 и 5.
5. Сравните числа a = –3,472 и b = –3,742.
А . a = b. Б . a < b. В . a > b. Г . Сравнить нельзя.
6. Упростите выражение 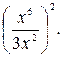
А. 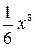 . Б.
. Б. 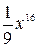 . В.
. В. 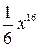 . Г.
. Г. 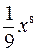 .
.
7. Упростите выражение 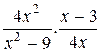 .
.
А. 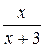 . Б.
. Б. 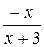 . В.
. В. 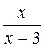 . Г.
. Г. 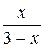 .
.
8. Укажите все значения x, при которых имеет смысл выражение 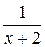 .
.
А. х > –2. Б. x < –2. В. x ¹ 2. Г. x ¹ –2.
9. Из формулы s = 2 + v × t выразите переменную t .
А. t = 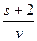 . Б. t = vЧ(s – 2). В.
. Б. t = vЧ(s – 2). В. 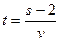 . Г.
. Г. 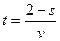 .
.
10. Корнями уравнения (x – 2)(х + 3) = 0 являются числа …
А. 2 и 3. Б. –2 и 3. В. –2 и –3. Г. 2 и –3.
11. Сравните числа а и b, если b – a = 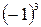 .
.
А . а < b. Б . a > b. В . a = b. Г . a 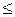 b.
b.
12. График функции у = 3х – 2 проходит через точку…
 А.(–1; –5). Б.(–1; 5). В.
А.(–1; –5). Б.(–1; 5). В. 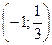 . Г.(–1;1)
. Г.(–1;1)
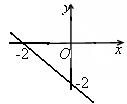
13. На рисунке изображен график функции …
А . y = x + 2. Б . y = –x + 2. В . y = –x – 2. Г . y = x – 2.
14. На рисунке представлен график движения пешехода из пункта А в пункт В, где s – расстояние от пешехода до пункта В, t — время движения. Сколько километров пройдено пешеходом до привала?
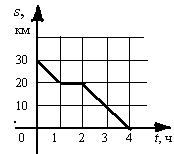 А. 20 км. Б. 10 км. В. 1 км. Г. 2 км.
А. 20 км. Б. 10 км. В. 1 км. Г. 2 км.
15. В классе 20% учащихся изучают только английский язык, 32% — только французский, а остальные 12 человек — только немецкий. Сколько учеников в классе?
А. 24. Б. 20. В. 32. Г. 25.
16. Какая из точек А(2;–5), В(3;2), С(–4;1), D(–1;–2) расположена ближе всех к оси х?
А. A. Б. B. В. C. Г. D.
17. Через точку А(2; –3) проведена прямая, параллельная оси у. Точка ее пересечения с осью х имеет координаты…
А. (0; 2). Б. (2; 0). В. (0; –3). Г. (–3; 0).
18. Из одной точки, лежащей вне прямой, проведены к этой прямой перпендикуляр и наклонная длиной 13 см, проекция которой равна 9 см. Найдите длину перпендикуляра.
А. 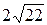 см. Б.
см. Б. 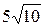 см. В. 44 см. Г. 125 см.
см. В. 44 см. Г. 125 см.
19. В прямоугольном треугольнике АВС угол А равен 69°. Сравните катеты АС и ВС.
A. AC < BC. Б . AC = BC. B. AC > BC. Г. Сравнить нельзя.
20. Углы параллелограмма не могут быть равными ...
А. 35° и 145°. Б. 50° и 130°. В. 20° и 70°. Г. 75° и 105°.
21. Если в прямоугольнике угол между диагональю и меньшей стороной равен 60º, а меньшая сторона равна 12 см, то диагональ прямоугольника равна ...
А. 18 см. Б. 12 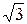 см. В. 24
см. В. 24 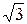 см. Г. 24 см.
см. Г. 24 см.
22. Сколько диагоналей можно провести из одной вершины семиугольника?
А. 5. Б. 4. В. 3. Г. Ответ отличен от приведенных.
23. Из точки, лежащей вне круга, проведены к окружности, ограничивающей этот круг, две взаимно перпендикулярные касательные, длиной 9 см каждая. Диаметр круга равен …
А. 4,5 см. Б. 9 см. В. 18 см. Г. величине, отличной от приведенных.
24. Как изменится площадь прямоугольного треугольника, если один катет увеличить в 2 раза, а другой уменьшить в 4 раза?
А. Увеличится в 2 раза. Б. Уменьшится в 2 раза.
В. Уменьшится в 3 раза. Г. Не изменится.
25. В круге диаметром 20 см проведена хорда длиной 12 см. Ее расстояние от центра равно ...
А. 8 см Б. 16 см. В. 4 см. Г. величине, отличной от приведенных.
Подсказки к заданиям базового уровня
1. Преобразуйте смешанное число в неправильную дробь. Воспользуйтесь правилом возведения дроби в степень:
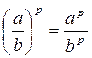 .
.
2. Воспользуйтесь определением квадратного корня, определением арифметического квадратного корня и следствием из него.
Основной уровень Вариант 1
1. Вычислите: 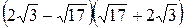 .
.
А. –11. Б. 11. В. 5. Г. –5
2. Вычислите значение выражения 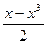 при x = –
при x = – 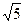 .
.
А. 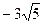 . Б.
. Б. 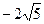 . В.
. В. 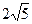 . Г.
. Г. 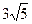 .
.
3. Найдите значение выражения 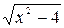 при
при 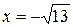 .
.
А. 3. Б. –3. В. ± 3. Г. Не имеет смысла.
4. Расположите в порядке возрастания числа 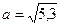 ,
, 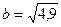 ,
, 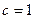 .
.
А . c < a < b. Б . c < b < a. В . b < c < a. Г. b < a < c.
5. Сравните числа 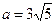 и
и 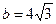 .
.
А. a < b. Б. a = b. В. a > b. Г. Сравнить нельзя.
6. Упростите выражение 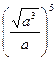 .
.
А. 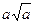 . Б.
. Б. 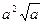 . В.
. В. 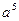 . Г.
. Г. 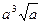 .
.
7. Упростите выражение 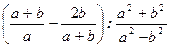 .
.
А. 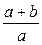 . Б.
. Б. 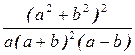 . В.
. В. 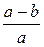 . Г.
. Г. 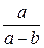 .
.
8. Укажите все значения x, при которых имеет смысл выражение 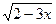 .
.
А. 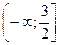 . Б.
. Б. 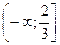 . В.
. В. 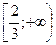 . Г.
. Г. 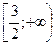 .
.
9. В цепи электрического тока два сопротивления R1 и R2 соединены параллельно. Общее сопротивление R связано с R1 и R2 формулой 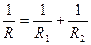 . Выразите R через R1 и R2.
. Выразите R через R1 и R2.
А. 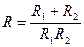 . Б.
. Б. 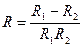 . В.
. В. 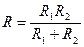 . Г.
. Г. 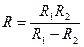 .
.
10. Один из корней уравнения 18x2 + 23x + 5 = 0 равен –1. Второй его корень равен … А. 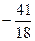 . Б.
. Б. 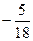 . В.
. В. 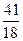 . Г.
. Г. 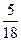 .
.
11. Сравните числа а и b, если разность b – a представляет собой квадрат некоторого числа.
А. a = b. Б. a £ b. В. a > b. Г. Сравнить нельзя.
12. Задайте формулой обратную пропорциональность, зная, что ее график проходит через точку с координатами (–3; 4).
А. 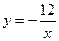 . Б.
. Б. 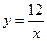 . В.
. В. 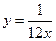 . Г.
. Г. 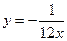 .
.
13. Какой из приведенных графиков может быть графиком функции 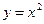 ?
?

14. 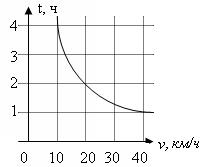
 На рисунке дан график зависимости времени t, затрачиваемого на путь из пункта А в пункт В, от скорости v движения, представляющей собой обратную пропорциональность. Какое время понадобится на путь из А в В, если двигаться со скоростью, меньшей 10 км/ч?
На рисунке дан график зависимости времени t, затрачиваемого на путь из пункта А в пункт В, от скорости v движения, представляющей собой обратную пропорциональность. Какое время понадобится на путь из А в В, если двигаться со скоростью, меньшей 10 км/ч?
А. 4 часа. Б. Меньше 4 ч. В. Больше 4 ч.
Г. Определить нельзя.
15. Смешали 2 литра 25% раствора кислоты и 4 литра 10% раствора той же кислоты. Концентрация полученного раствора равна …
А. 35%. Б. 15%. В. 17,5%. Г. 20%.
16. Какая из приведенных точек находится на том же расстоянии от оси x, что и точка с координатами (–3;4)?
 А. (–3; 2). Б. (3; 1). В. (–4; –3). Г. (–1; 4).
А. (–3; 2). Б. (3; 1). В. (–4; –3). Г. (–1; 4).
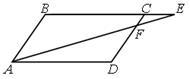
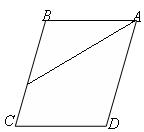
17. На рисунке ABCD — параллелограмм, AD = 12 см, CE = 4 см. Отношение площадей треугольников ABE и CFE равно...
А. 4:1. Б. 8:1. В. 64:1. Г. 16:1.
18. В прямоугольной трапеции основания равны 5 см и 17 см, а большая боковая сторона 13 см. Высота трапеции равна …
А. 12 см. Б. 11 см. В. 5 см. Г. 8 см.
19. В равнобедренном треугольнике угол при основании равен 70°. Сравните высоту h и половину основания 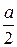 .
.
А. Сравнить нельзя. Б. 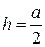 . В.
. В. 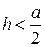 . Г.
. Г. 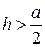 .
.
20. Два неравных отрезка в точке пересечения делятся пополам, их концы последовательно соединены. Полученный четырехугольник является …
А. параллелограммом. Б. ромбом. В. прямоугольником. Г. квадратом.
21. Сторона ромба равна 6 см, острый угол 60°. Диагонали ромба равны …
А. 6 и 12 см. Б. 6 и 6 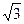 см. В. 3 и 3
см. В. 3 и 3 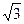 см. Г. 3 и 6
см. Г. 3 и 6 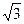 см.
см.
22. Две параллельные прямые пересечены тремя параллельными прямыми. Сколько образовалось параллелограммов?
А. 6. Б. 4. В. 2. Г. 3.
23. Четырехугольник ABCD — прямоугольная трапеция (АВ ^ AD, ÐAD С — тупой), АС — ее диагональ, MN — средняя линия, M Î AB, N Î CD, K — точка пересечения АС и MN. Сравните отрезки MK и NK.
А . MK > NK. Б . MK = NK. В. MK < NK. Г. Сравнить нельзя.
24. 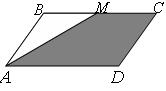 Площадь параллелограмма ABCD равна S, MB = MC. Чему равна площадь закрашенной фигуры?
Площадь параллелограмма ABCD равна S, MB = MC. Чему равна площадь закрашенной фигуры?
А. 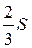 . Б.
. Б. 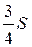 . В.
. В. 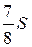 . Г.
. Г. 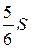 .
.
25. В прямоугольной трапеции основания равны 10 и 6 см, а большая боковая сторона равна 5 см. Площадь трапеции равна ...
А. 48 см2. Б. 24 см2. В. 12 см2. Г. 36 см2.
Основной уровень Вариант 2
1. Вычислите: 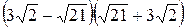 .
.
А. 3. Б. 15. В. –3. Г. –15.
2. Вычислите значение выражения 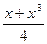 при
при 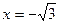 .
.
А. 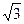 . Б.
. Б. 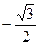 . В.
. В. 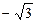 . Г.
. Г. 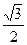 .
.
3. Найдите значение выражения 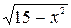 при
при 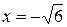 .
.
А. 3. Б. –3. В. ± 3. Г. Не имеет смысла.
4. Расположите в порядке возрастания числа 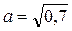 ,
, 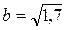 ,
, 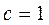 .
.
А . а < b < c. Б . c < a < b. В . c < b < a. Г . a < c < b.
5. Сравните числа 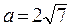 и
и 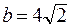 .
.
А. Сравнить нельзя. Б. a = b . В. a > b. Г. a < b.
6. Упростите выражение 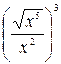 .
.
А. 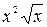 . Б.
. Б. 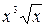 . В.
. В. 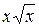 . Г.
. Г. 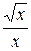 .
.
7. Упростите выражение 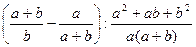 .
.
А. 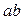 . Б.
. Б. 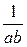 . В.
. В. 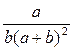 . Г.
. Г. 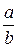 .
.
8. Укажите все значения x, при которых имеет смысл выражение 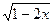 .
.
А. 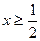 . Б.
. Б. 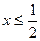 . В.
. В. 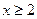 . Г.
. Г. 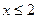 .
.
9. В цепи электрического тока два сопротивления R1 и R2 соединены параллельно. Общее сопротивление R связано с R1 и R2 формулой 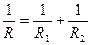 . Выразите R1 через R и R2.
. Выразите R1 через R и R2.
А. 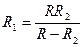 . Б.
. Б. 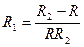 . В.
. В. 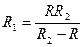 . Г.
. Г. 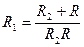 .
.
10. Один из корней уравнения 28x2 + 23x – 5 = 0 равен –1. Второй его корень равен …
А. 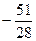 . Б.
. Б. 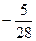 . В.
. В. 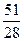 . Г.
. Г. 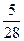 .
.
11. Сравните числа а и b, если разность a – b является квадратом некоторого числа.
А. a < b. Б. a = b. В. a ³ b. Г. Сравнить нельзя.
12. Задайте формулой обратную пропорциональность, зная, что ее график проходит через точку с координатами (–25; –0,2).
А. 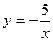 . Б.
. Б. 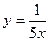 . В.
. В. 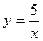 . Г.
. Г. 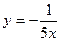 .
.
13. Какой из приведенных графиков может быть графиком функции 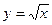 ?
?

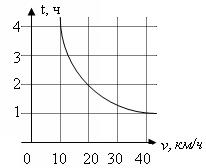
14.  На рисунке дан график зависимости времени t, затрачиваемого на путь из пункта А в пункт В, от скорости v движения, представляющей собой обратную пропорциональность. С какой скоростью v надо двигаться, чтобы добраться из А в В менее, чем за 2 часа ?
На рисунке дан график зависимости времени t, затрачиваемого на путь из пункта А в пункт В, от скорости v движения, представляющей собой обратную пропорциональность. С какой скоростью v надо двигаться, чтобы добраться из А в В менее, чем за 2 часа ?
А. v = 20 км/ч. Б. v < 20 км/ч. В. v > 20 км/ч.
Г. Определить нельзя.
15. Смешали 5 литров 20% раствора кислоты и 3 литра 40% раствора той же кислоты. Концентрация полученного раствора равна …
А. 30%. Б. 25%. В. 35%. Г. 27,5%.
16.  Какая из приведенных точек находится на том же расстоянии от оси y, что и точка с координатами (–2; 3)?
Какая из приведенных точек находится на том же расстоянии от оси y, что и точка с координатами (–2; 3)?
А. (1; 3). Б. (1; –3). В. (–2; –2). Г. (–3; 2).
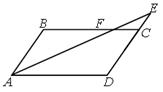
17. На рисунке ABCD — параллелограмм, AB = 8 см, CE = 2 см. Отношение площадей треугольников ADE и FCE равно ...
А. 20:1. Б. 40:1. В. 25:1. Г. 45:2.
18. В равнобедренном треугольнике основание и боковая сторона равны соответственно 12 см и 10 см. Высота, опущенная на его основание, равна …
А. 6 см. Б. 13 см. В. 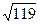 см. Г. 8 см.
см. Г. 8 см.
19. Из вершины В тупого угла равнобедренной трапеции АВС D проведён перпендикуляр В F на основание AD. ÐВ AD = 41°. Сравните длины отрезков А F и BF.
А. Сравнить нельзя. Б. BF = AF. В . BF > AF. Г . BF < AF.
20. Два равных отрезка в точке пересечения делятся пополам, их концы последовательно соединены отрезками. Полученный четырехугольник является …
А. трапецией. Б. квадратом. В. ромбом. Г. прямоугольником.
21. Меньшая сторона прямоугольника равна 3 дм, а угол между диагоналями равен 120°. Большая сторона прямоугольника и его диагональ соответственно равны …
А. 6 дм, 3 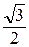 дм. Б. 3
дм. Б. 3 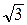 дм, 6 дм. В. 3
дм, 6 дм. В. 3 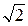 дм, 3 дм. Г. 5 дм, 3
дм, 3 дм. Г. 5 дм, 3 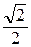 дм.
дм.
22. Три параллельные прямые пересечены тремя параллельными прямыми. Сколько получилось параллелограммов?
А. 4. Б. 6. В. 8. Г. 9.
23. 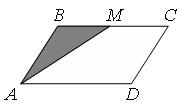 Четырёхугольник ABCD — трапеция (ВС ½½ AD), ВС < AD, АС — ее диагональ, MN — средняя линия, M Î AB, N Î CD, K — точка пересечения AC и MN. Сравните отрезки M K и N K.
Четырёхугольник ABCD — трапеция (ВС ½½ AD), ВС < AD, АС — ее диагональ, MN — средняя линия, M Î AB, N Î CD, K — точка пересечения AC и MN. Сравните отрезки M K и N K.
А. MK = NK. Б. MK < NK. В. MK > NK. Г. Сравнить нельзя.
24. Площадь параллелограмма ABCD равна S, M — середина стороны BC. Чему равна площадь закрашенной фигуры?
А. 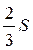 . Б.
. Б. 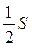 . В.
. В. 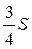 . Г.
. Г. 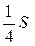 .
.
25. В прямоугольной трапеции основания равны 20 и 12 см, а меньшая диагональ равна 13 см. Площадь трапеции равна ...
А. 160 см2. Б. 40 см2. В. 96 см2. Г. 80 см2.
Основной уровень. Вариант 3.
1. Вычислите: 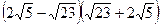 .
.
А. –3. Б. 13. В. 3. Г. –13.
2. Вычислите значение выражения 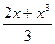 при x =
при x = 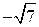 .
.  .
.
А. 3 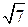 . Б.
. Б. 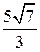 . В. –3
. В. –3 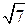 . Г. –
. Г. – 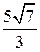 .
.
3. Найдите значение выражения 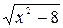 при
при 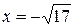 .
.
А. –3. Б. 3. В. ± 3. Г. Не имеет смысла.
4. Расположите числа 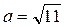 ,
, 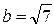 , с = 3 в порядке убывания.
, с = 3 в порядке убывания.
А . a > b > c. Б . с > a > b. В . с > b > a. Г. a > c > b.
5. Сравните числа 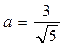 и
и 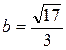 .
.
А. a = b. Б. a < b. В. a > b. Г. Сравнить нельзя.
6. Упростите выражение 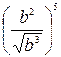 .
.
А. 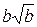 . Б.
. Б. 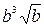 . В.
. В. 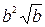 . Г.
. Г. 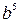 .
.
7. Упростите выражение 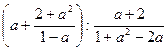 .
.
А. a – 1. Б. a + 1. В. 1 – a. Г. 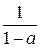 .
.
8. Укажите все значения x, при которых выражение 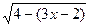 не имеет смысла.
не имеет смысла.
А. 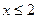 . Б.
. Б. 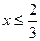 . В.
. В. 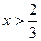 . Г.
. Г. 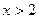 .
.
9. Из формулы 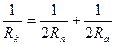 дающей соотношение между радиусом кривизны Rk орбиты и расстояниями перигея R п и апогея R а от центра Земли, выразите Rn через остальные переменные.
дающей соотношение между радиусом кривизны Rk орбиты и расстояниями перигея R п и апогея R а от центра Земли, выразите Rn через остальные переменные.
А. 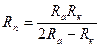 . Б.
. Б. 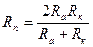 . В.
. В. 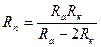 . Г.
. Г. 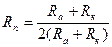 .
.
10. Один из корней уравнения 3x2 – 7x + 2 = 0 равен 2. Второй его корень равен …
А. 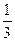 . Б.
. Б. 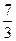 . В.
. В. 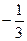 . Г.
. Г. 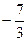 .
.
11. Сравните числа а и b, если разность b – a представляет собой куб положительного числа.
А. a = b. Б. a > b. В. a < b. Г. Сравнить нельзя.
12. 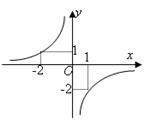 На рисунке изображен график функции y =
На рисунке изображен график функции y = 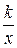 . Коэффициент k равен ...
. Коэффициент k равен ...
A . – 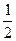 . Б. 2. В.
. Б. 2. В. 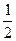 . Г. –2.
. Г. –2.
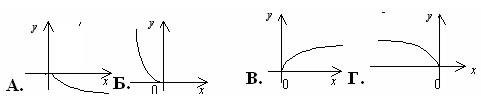
13. На каком рисунке изображен график функции y = 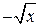 ?
?
14. 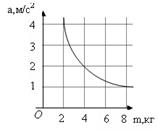
 На рисунке дан график зависимости ускорения а движущегося тела от его массы m при постоянной силе F, действующей на это тело (F = ma). Каким ускорением обладает тело, масса которого меньше 4 кг?
На рисунке дан график зависимости ускорения а движущегося тела от его массы m при постоянной силе F, действующей на это тело (F = ma). Каким ускорением обладает тело, масса которого меньше 4 кг?
А. a = 2 м/с2. Б. a < 2 м/с2. В. a > 2 м/с2. Г. Определить нельзя.
15. Два литра некоторого фруктового сока имеют концентрацию сахара 10%, а три литра другого — 15%. Какова концентрация сахара в их смеси?
А. 25 %. Б. 13 %. В. 12,5 %. Г. 5 %.
16.  Какая из приведенных точек находится на том же расстоянии от начала координат, что и точка (8; –6)?
Какая из приведенных точек находится на том же расстоянии от начала координат, что и точка (8; –6)?
А. (4; 3). Б. (–6;10). В. (–8; –6). Г. (10; 6).
17. На рисунке ABCD – параллелограмм. AD = 12 см, CE = 4 см, CF = 2 см. Длина стороны AB равна ...
А. 6 см. Б. 9 см. В. 10 см. Г. 8 см.
18. Основания прямоугольной трапеции равны 10 см и 15 см, большая боковая сторона равна 13 см. Меньшая боковая сторона трапеции равна …
А.6 см Б.7,5 см. В.10 см. Г.12 см.
19. Из вершины С тупого угла прямоугольной трапеции АВС D проведён перпендикуляр С F на основание AD. ÐADC = 47°. Сравните длины отрезков А B и DF.
А. Сравнить нельзя. Б. DF = AB. В . DF > AB. Г . DF < AB.
20. Какую фигуру образуют прямые, последовательно соединяющие середины сторон прямоугольника?
А. Прямоугольник. Б. Квадрат. В. Ромб. Г. Трапецию.
21. В равнобедренной трапеции острый угол равен 60°, боковая сторона равна 8 см, а большее основание 14 см. Средняя линия и высота трапеции соответственно равны …
А. 6 см и 2 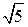 см. Б. 11 см и 4
см. Б. 11 см и 4 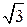 см. В. 10 см и 4
см. В. 10 см и 4 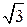 см. Г. 9 см и 2
см. Г. 9 см и 2 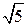 см.
см.
22. Два луча, выходящие из одной точки, пересечены тремя параллельными прямыми. Сколько при этом получилось трапеций?
А. 2. Б. 3. В. 4. Г. 6.
23. Четырехугольник ABCD — прямоугольная трапеция (АВ ^ AD, ÐAD С — тупой), BD — ее диагональ, MN — средняя линия, M Î AB, N Î CD, K — точка пересечения BD и MN. Сравните отрезки MK и NK.
А. Сравнить нельзя. Б. MK = NK. В. MK > NK. Г. MK < NK.
24. 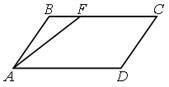 В параллелограмме ABCD BF:FC = 1:3. Площади треугольника ABF и четырехугольника AFCD относятся как ...
В параллелограмме ABCD BF:FC = 1:3. Площади треугольника ABF и четырехугольника AFCD относятся как ...
А. 1:3. Б. 1:9. В. 1:5. Г. 1:7.
25. В равнобедренной трапеции основания равны 4 см и 20 см, а боковая сторона равна 10 см. Площадь трапеции равна ...
А. 144 см2. Б. 36 см2. В. 72 см2. Г. 96 см2.
Подсказки к заданиям основного уровня
1. Воспользуйтесь формулой произведения разности двух выражений и их суммы, правилом возведения произведения в степень и следствием из определения арифметического квадратного корня.
Произведение разности двух выражений и их суммы равно разности квадратов этих выражений: ( a – b )( a + b ) = a 2 – b 2 .
Для любых чисел а и b и произвольного натурального числа n имеет место равенство ( ab ) n = anbn .
При любом а, при котором выражение 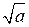 имеет смысл, справедливо равенство
имеет смысл, справедливо равенство 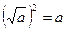 .
.
2. Вначале преобразуйте данное выражение, выполнив вынесение общего множителя в числителе за скобки, затем подставьте заданное значение переменной. Воспользуйтесь следствием из определения арифметического квадратного корня.
Для разложения многочлена на множители способом вынесения общего множителя за скобки нужно:
1) в членах многочлена выделить общий множитель;
Продвинутый уровень. Вариант 2.
1. О натуральных числах m и n известно, что m > n . Расположите в порядке возрастания числа a = 1, 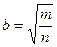 ,
, 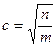 .
.
А . с < b < a. Б . a < b < c. В . с < a < b. Г . а < c < b.
2. Упростите выражение 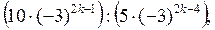 где k — натуральное число.
где k — натуральное число.
А. 54. Б. –54. В. –18. Г. 18.
3. Сравните числа 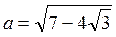 и
и 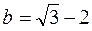 .
.
А. а > b. Б. а = b. В. a < b. Г. Сравнить нельзя.
4. Чему равно выражение 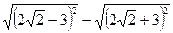 ?
?
А. –6. Б. 6. В. 4 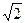 . Г. – 4
. Г. – 4 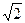 .
.
5. Укажите наименьшее целое число x, при котором справедливо равенство
|–x – 1| = 1 + x.
А. 1. Б. –1. В. 0. Г. Такого числа не существует.
6. Уравнение x2 + px + q = 0 не имеет корней. Сколько корней будет иметь уравнение, полученное из данного увеличением его свободного члена?
А. Одно. Б. Два. В. Ни одного. Г. Однозначного ответа нет.
7. Квадратное уравнение x2 – bx – с = 0 имеет корень, равный –1, если …
А. b – c = –1. Б. b – c = 1. В. b = – c. Г. b – c = 0.
8. Укажите все значения a, при которых квадратный трехчлен ax2 + 2x + 3 имеет корни разных знаков.
А. a £ 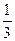 . Б. а >
. Б. а > 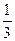 . В. a > 0. Г. a < 0.
. В. a > 0. Г. a < 0.
9. Сколько существует точек на графике функции y = 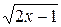 , у которых абсцисса и ордината совпадают?
, у которых абсцисса и ордината совпадают?
А. Ни одной. Б. Одна. В. Две. Г. Три.
10. Какую прямую из приведенных в ответах пересекает график функции 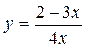 ?
?
А. x = 0. Б. y = – 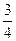 . В. x =
. В. x = 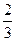 . Г. Среди приведенных такой прямой нет
. Г. Среди приведенных такой прямой нет
11. 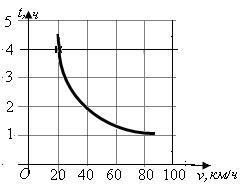 На рисунке дан график зависимости времени t, затрачиваемого на путь из пункта А в пункт В, от скорости движения v, представляющей собой обратную пропорциональную зависимость. Каково расстояние между пунктами А и В?
На рисунке дан график зависимости времени t, затрачиваемого на путь из пункта А в пункт В, от скорости движения v, представляющей собой обратную пропорциональную зависимость. Каково расстояние между пунктами А и В?
А. 40 км. Б. 60 км. В. 100 км. Г. 80 км.
12. В бассейн проведена труба. Вследствие засорения её приток воды уменьшился на 60%. На сколько процентов вследствие этого увеличится время, необходимое для заполнения бассейна?
А. На 150%. Б. На 50%. В. На 250%. Г. На 60%.
13. Какой вид имеет треугольник, отсекаемый биссектрисой острого угла равнобедренной трапеции, если боковая сторона меньше меньшего основания трапеции?
А. Прямоугольный. Б. Остроугольный. В. Равнобедренный. Г. Разносторонний.
14. Биссектрисы углов параллелограмма пересекают его стороны в точках M , N , P и Q. Четырехугольник MNPQ является …
А. трапецией. Б. прямоугольником. В. параллелограммом. Г. ромбом.
15. 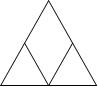 В равнобедренный треугольник вписан параллелограмм так, что угол параллелограмма совпадает с углом при вершине треугольника, а вершина противоположного угла лежит на основании. Боковая сторона треугольника равна 8 см. Периметр параллелограмма равен …
В равнобедренный треугольник вписан параллелограмм так, что угол параллелограмма совпадает с углом при вершине треугольника, а вершина противоположного угла лежит на основании. Боковая сторона треугольника равна 8 см. Периметр параллелограмма равен …
А.16 см. Б.24 см. В.12 см. Г.8 см.
16.  Гипотенуза равнобедренного прямоугольного треугольника равна с. Его катет равен …
Гипотенуза равнобедренного прямоугольного треугольника равна с. Его катет равен …
А. 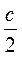 . Б.
. Б. 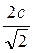 . В.
. В. 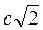 . Г.
. Г. 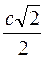 .
.
17. Биссектриса угла А в параллелограмме АВС D делит сторону ВС на отрезки 7 см и 14 см (считая от вершины С). Периметр параллелограмма равен …
А. 56 см. Б. 70 см. В. 42 см. Г. 35 см.
18. 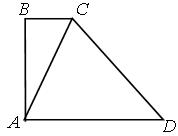 Дан треугольник АВС, площадь которого S, О — точка пересечения медиан А K и ВD (KÎBС, DÎАС). Площадь треугольника АОD равна…
Дан треугольник АВС, площадь которого S, О — точка пересечения медиан А K и ВD (KÎBС, DÎАС). Площадь треугольника АОD равна…
А. 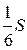 . Б.
. Б. 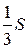 . В.
. В. 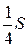 . Г.
. Г. 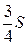 .
.
19. Если АВСD — трапеция (АD||ВС), ÐBАС = ÐCDА, BC = 2, АD = 8, то диагональ АС равна …
А. 5. Б. 4. В. 3. Г. 6.
20. Совокупность точек плоскости, удаленных от двух параллельных прямых на одно и то же расстояние, образует …
А. прямую. Б. две прямые. В. полосу. Г. окружность.
Продвинутый уровень. Вариант 3.
1. О натуральных числах a и b известно, что a < b. Расположите в порядке убывания числа x = 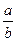 , y =
, y = 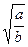 , z =
, z = 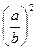 .
.
А . z > y > x. Б . y > z > x. В . z > x > y. Г . y > x > z.
2. Упростите выражение 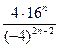 .
.
А. 64. Б. –64. В. 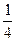 . Г. –
. Г. – 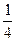 .
.
3. Сравните числа 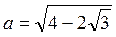 и
и 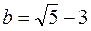 .
.
А. a = b. Б. a < b. В. a > b. Г. Сравнить нельзя.
4. Чему равно выражение 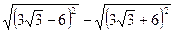 ?
?
А. –12. Б. 12. В. 6 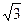 . Г. –6
. Г. –6 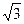 .
.
5. Укажите наибольшее целое число х, при котором справедливо равенство
|x + 1| = –1 – x.
А. Не существует. Б. –1. В. 1. Г. 0.
6. Уравнение x2 + px + q = 0 имеет 2 корня. Сколько корней будет иметь уравнение, полученное из данного увеличением его свободного члена?
А. 0. Б. 1. В. 2. Г. Однозначного ответа нет.
7. Квадратное уравнение а x2 – x – с = 0 имеет корень, равный –2, если …
А. 4а – c = –2. Б. 4а – c = 2. В. 4а = – c + 2. Г. 4а – c = 0.
8. Укажите все значения b и с, при которых квадратный трехчлен 2x2 + bx + c имеет противоположные корни.
А. b = 0, c > 0. Б. b = 0, c < 0. В. c < 0, b — любое. Г. b ¹ 0, c — любое.
9. Сколько общих точек имеют графики функций 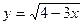 и y = - x?
и y = - x?
А. 3. Б. 2. В. 1. Г. 0.
10. График функции y= 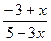 не имеет общих точек с прямой …
не имеет общих точек с прямой …
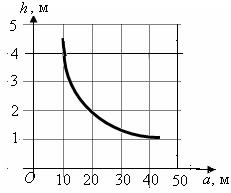 А. x = 3. Б. y =
А. x = 3. Б. y = 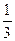 . В. x =
. В. x = 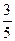 . Г. у = –
. Г. у = – 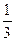 .
.
11. На рисунке дан график зависимости между стороной а и высотой h параллелограмма постоянной площади (S = ah). Площадь параллелограмма равна …
А. 10 м2. Б. 20 м2. В. 30 м2. Г. 40 м2.
12. Благодаря внедрению рационализаторского предложения время, необходимое для изготовления некоторой детали, уменьшилось на 20%. На сколько процентов увеличилась производительность труда?
А. На 25%. Б. На 20%. В. На 125%. Г. На 75%.
13. Какой вид имеет треугольник, отсекаемый биссектрисой угла параллелограмма, равного 120°?
А. Прямоугольный. Б. Тупоугольный.
В. Равносторонний. Г. Разносторонний.
14. 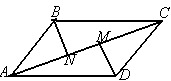 В параллелограмме АВС D перпендикуляры, проведенные через вершины тупых углов к диагонали АС, пересекают ее в точках М и N. Четырехугольник BND М является …
В параллелограмме АВС D перпендикуляры, проведенные через вершины тупых углов к диагонали АС, пересекают ее в точках М и N. Четырехугольник BND М является …
А. параллелограммом. Б. прямоугольником.
 В. ромбом. Г. трапецией.
В. ромбом. Г. трапецией.
15. В равнобедренный прямоугольный треугольник вписан прямоугольник так, что один угол у них общий. Катет треугольника равен 8 см. Периметр прямоугольника равен …
А. 8 см. Б. 12 см. В. 24 см. Г. 16 см.
16. Сторона равностороннего треугольника равна а. Его высота равна …
А. 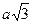 . Б.
. Б. 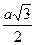 . В.
. В. 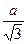 . Г.
. Г. 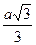 .
.
17. Биссектриса угла прямоугольника делит сторону пополам, а периметр его равен 60 см. Вычислите стороны прямоугольника.
А. По 15 см. Б. 10 и 20 см. В. 12 и 18 см. Г. 6 и 24 см.
18. Дан треугольник АВС, площадь которого равна S, О — точка пересечения медиан АD и ВЕ (DÎВС, ЕÎАС). Найдите площадь четырехугольника ODCE.
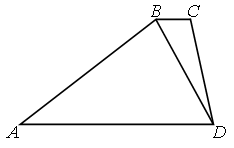 А.
А. 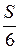 . Б.
. Б. 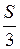 . В.
. В. 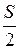 . Г.
. Г. 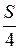 .
.
19. Если АВСD — трапеция с основаниями AD и ВС, ÐBАD = ÐBDС, AD = 16, BC = 4, то диагональ BD равна …
А. 5. Б. 6. В. 7. Г. 8.
20. Совокупность точек плоскости, удаленных от двух точек на одно и то же расстояние, образует…
А. окружность. Б. прямую. В. две прямые. Г. полосу.
Подсказки к заданиям продвинутого уровня
1. Воспользуйтесь следующими свойствами функций у = 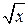 и у = х2.
и у = х2.
Если 0 < x < 1, то 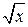 > x ; если х > 1, то
> x ; если х > 1, то 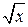 < x .
< x .
Если 0 < x < 1, то x 2 < x ; если х > 1, то x 2 > x .
Сравните данные дроби с 1, а затем примените приведенные свойства.
2. Примените правила действий над одночленами и степенями с одинаковыми основаниями.
3. Установите знаки а и b. Помните, что знаком 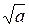 обозначают арифметическое значение корня.
обозначают арифметическое значение корня.
4. Воспользуйтесь следующим утверждением.
При любом значении а верно равенство 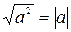 .
.
Установите знаки выражений, стоящих в скобках.
5. Воспользуйтесь следующими утверждениями.
Модуль положительного числа равен этому числу;
Модуль нуля равен нулю.
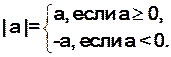
Установите знак выражения, стоящего под знаком модуля, запишите соответствующее неравенство, из которого можно найти искомое значение х.
6. Воспользуйтесь определением дискриминанта квадратного уравнения и условиями, при которых это уравнение имеет 2, 1, 0 корней.
Дискриминантом квадратного уравнения ах 2 + bx + c = 0 называют выражениеD = b 2 – 4ас.
При D > 0 квадратное уравнение имеет два корня; при D = 0 — один корень;
при D < 0 квадратное уравнение корней не имеет.
Вначале запишите выражение для дискриминанта и установите его знак. Подумайте, что произойдет с дискриминантом, если изменить, согласно условию, свободный член уравнения.
7. Примените определение корня уравнения.
Число х 0 называют корнем уравнения f ( x ) = 0, если f ( x 0 ) = 0.
8. Используйте теорему Виета.
Сумма корней приведенного квадратного уравнения х2 + рх + q = 0 равна второму коэффициенту, взятому с обратным знаком, а произведение корней равно свободному члену: х1 + х2 = –р; х1 × х 2 = q .
Не забывайте о знаке дискриминанта.
9. Решение задания сводится к составлению и решению уравнения.
Уравнение вида 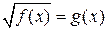 решается возведением обеих частей в квадрат с последующей проверкой найденных корней.
решается возведением обеих частей в квадрат с последующей проверкой найденных корней.
10. Результат можно получить подстановкой предлагаемых ответов в условие.
11. В задании рассматривается обратная пропорциональная зависимость вида 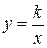 , где k — постоянная. Требуется найти эту постоянную: k = xy. Значения абсциссы и ординаты находятся из графика.
, где k — постоянная. Требуется найти эту постоянную: k = xy. Значения абсциссы и ординаты находятся из графика.
12. Воспользуйтесь правилами нахождения процента от значения величины, процентного отношения двух значений.
Если значение а величины увеличить на р%, то полученное значение будет равно
а + 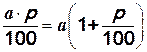
| В библиотеке к началу года было 8000 книг. За год количество книг в библиотеке увеличилось на 10 %. В библиотеке стало 8000× 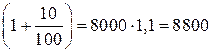 книг. книг.
|
Если значение а величины уменьшить на р%, то полученное значение будет равно
а – 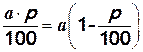
| Зарплата работника составляет 4 600 зедов в месяц. Его заработок облагается подоходным налогом, который составляет 13 % зарплаты. За месяц работы работник получит 4 600× 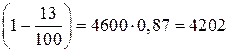 зеда. зеда.
|
Если значение величины увеличилось от а до b , то оно увеличилось на 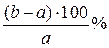 . .
| Цена товара увеличилась с 1400 руб. до 1750 руб. Она увеличилась на 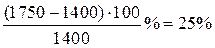
|
Если значение величины уменьшилось от а до b , то оно уменьшилось на 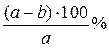 . .
| Цена товара снизилась с 1750 руб. до 1400 руб. Она снизилась на 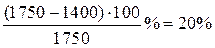 . .
|
Воспользуйтесь связью между величинами, приведенными в условии.
13. Воспользуйтесь определением биссектрисы угла и свойством параллельных прямых.
Если две параллельные прямые пересекает третья, то внутренние разносторонние (накрест лежащие) углы равны.
Используйте утверждение: если каждая из двух величин равна третьей, то они равны между собой.
14. Воспользуйтесь определением или одним из признаков параллелограмма.
Параллелограммом называется четырёхугольник, противоположные стороны которого попарно параллельны.
Если две противоположные стороны четырёхугольника параллельны и равны, то этот четырёхугольник — параллелограмм.
Если противоположные стороны четырёхугольника попарно равны, то этот четырёхугольник — параллелограмм.
Для доказательства равенства сторон параллелограмма примените признаки равенства треугольников.
15. Воспользуйтесь свойством параллельных прямых.
Если две параллельные прямые пересекает третья, то соответственные углы равны.
Докажите, что сумма длин двух смежных сторон параллелограмма равна боковой стороне треугольника.
16. Воспользуйтесь теоремой Пифагора.
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
17. Воспользуйтесь определением биссектрисы угла и свойством параллельных прямых.
Если две параллельные прямые пересекает третья, то внутренние разносторонние (накрест лежащие) углы равны.
Докажите, что образовавшийся треугольник является равнобедренным.
18. Воспользуйтесь определением медианы и следующими утверждениями.
Если два треугольника имеют общую вершину, а основания лежат на одной прямой, то их площади относятся, как длины оснований.
Медианы треугольника точкой пересечения делятся в отношении 2:1, считая от вершины.
Установите, что каждая медиана делит данный треугольник на два треугольника равной площади, а все три медианы делят его на 6 треугольников, имеющих равные площади.
19. Воспользуйтесь признаками подобия треугольников.
Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
Для установления равенства углов примените свойство параллельных прямых.
20. Выберите из следующих утверждений то, которое поможет ответить на вопрос задания.
Геометрическим местом точек, равноудалённых от сторон угла, является биссектриса этого угла.
Геометрическим местом точек, равноудалённых от концов отрезка, является серединный перпендикуляр к этому отрезку.
Геометрическим местом точек, равноудалённых от данной точки, является окружность с центром в этой точке.
Повышенный уровень. Вариант 1
1. Расположите в порядке убывания дроби 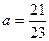 ,
, 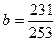 ,
, 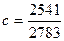 .
.
А . a = b = c. Б . a > b > c. В . c > b > a. Г . b > c > a.
2. Сравните 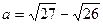 и b = 0,1.
и b = 0,1.
А. a = b. Б. a > b. В. a < b. Г. Без вычислительных средств сравнить нельзя.
3. Вычислите 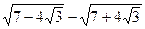 .
.
А. 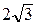 . Б. 4. В. –4. Г. –
. Б. 4. В. –4. Г. – 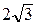 .
.
4. Укажите все значения x, при которых 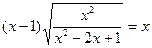 .
.
А. xÎ (1; +¥). Б. xÎ(–¥; 0] È(1; +¥). В. xÎ (0; 1). Г. xÎ (–¥; 0].
5. Сколько корней имеет уравнение 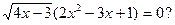
А. Ни одного. Б. Один. В. Два. Г. Три.
6. Уравнение ax2 + bx + c = 0 не имеет корней и a + b + c < 0. Какие знаки имеют числа а и с?
А. + +. Б. – +. В. + –. Г. – –.
7. Длина промежутка, состоящего из решений неравенства |3x – a| < 2 равна …
 А.
А. 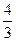 . Б.
. Б. 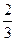 . В.
. В. 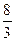 . Г.
. Г. 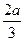 .
.
8. Укажите все значения а, при которых график функции y = ax + 1 – a имеет вид, изображенный на рисунке.
А. a > 0. Б. 0 < a < 1. В. a > 1. Г. Таких значений а не существует.
9. Множество решений уравнения y = x | y | изображено на рисунке …

10. Только что добытый каменный уголь содержит 2% воды, а после двухнедельного пребывания на воздухе он содержит 12% воды. Добыли 1 т угля. Через 2 недели его масса примерно составит … (выберите наиболее точное значение)
А. 1109 кг. Б. 1114 кг. В. 1120 кг. Г. 1086 кг.
11. Боковая сторона равнобедренного треугольника равна 6 см. Через один из концов основания и середину высоты, проведенной к основанию, проведена прямая до пересечения с боковой стороной. Расстояние от точки пересечения до вершины треугольника равно …
А.1,5 см. Б. 1 см. В. 2 см. Г. 3 см.
12. Высоты треугольника АВС пересекаются в точке О. Известно, что ОА = ВС. Угол ВАС равен …
А. 30°. Б. 45°. В. 60°. Г. 75°.
13. Отрезки, соединяющие середины смежных сторон равнобедренной трапеции, образуют квадрат. Основания трапеции равны 1 см и 7 см. Ее боковая сторона равна ...
А. 5 см. Б. 4 см. В. 3 см. Г. 3 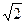 см.
см.
14. Дан четырёхугольник, A, B, C, D — последовательные середины его сторон, P, Q — середины диагоналей. Сравните углы BPC и AQD.
А. Ð BPC < Ð AQD. Б. Ð BPC = Ð AQD.
В. Ð BPC > Ð AQD. Г. Сравнить нельзя.
15. Сторона AD параллелограмма ABCD разделена на 5 равных частей. Первая точка деления Р соединена с вершиной В. Прямая ВР пересекает диагональ АС в точке Q. Отношение AC : AQ равно …
А. 4. Б. 5. В. 6. Г. числу, отличному от приведенных.
Повышенный уровень. Вариант 2.
1. Расположите дроби в порядке возрастания 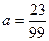 ,
, 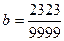 ,
, 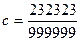 .
.
А . a = b = c. Б . a < b < c. В . c < b < a. Г . b < c < a.
2. Сравните 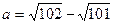 и b = 0,05.
и b = 0,05.
А. а > b. Б. а < b . В. a = b. Г. Без вычислительных средств сравнить нельзя.
3. Вычислите 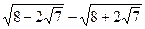 .
.
А. 2. Б. – 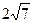 . В.
. В. 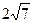 . Г. –2.
. Г. –2.
4. Укажите все значения x, при которых справедливо равенство 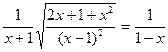 .
.
А.(–¥; 1). Б.(–1; +¥). В.(–¥; –1)È(1; + ¥). Г.(–1; 1).
5. Сколько корней имеет уравнение 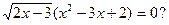
А. Ни одного. Б. Один. В. Два. Г. Три.
6. Уравнение ax2 + bx + c = 0 не имеет корней и a + b + c > 0. Какие знаки имеют числа а и с?
А. + +. Б. – +. В. + –. Г. – –.
7.  Длина промежутка, который состоит из решений неравенства |2x – 1| < a
Длина промежутка, который состоит из решений неравенства |2x – 1| < a
(a > 0) равна …
А. 1. Б. a. В. 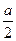 . Г. 2a.
. Г. 2a.
8. Укажите все значения а, при которых график функции y = ax+ 1 – a имеет вид, изображенный на рисунке.
А. Таких значений не существует. Б. a < 0. B . a > 1. Г. a < 1.
9.  Множество решений уравнения x = y | x | изображено на рисунке …
Множество решений уравнения x = y | x | изображено на рисунке …
10. Ягоды содержат 99% воды и 1% сухого вещества. При сушке часть воды испарилась, в результате чего воды стало 98%. Сколько сейчас весят ягоды, если до сушки они весили 100 кг?
А. 99 кг. Б. 98,99 кг. В. 98 кг. Г. 50 кг.
11. В треугольнике АВС сторона ВС равна 12 см. Через вершину А и середину медианы к стороне АС проведена прямая до пересечения с ВС в точке D. Отрезок CD равен …
А. 6 см. Б. 4 см. В. 9 см. Г. 8 см.
12. Высоты треугольника АВС пересекаются в точке О. Известно, что ОВ = АС. Угол АВС равен …
А. 30°. Б. 45°. В. 60°. Г. 75°.
13. Отрезки, соединяющие середины смежных сторон равнобедренной трапеции, образуют квадрат. Боковая сторона и меньшее основание соответственно равны 10 см и 2 см. Средняя линия трапеции равна …
А. 8 см. Б. 12 см. В. 6 см. Г. 14 см.
14. Дан четырёхугольник, A, B, C, D — последовательные середины его сторон, P, Q — середины диагоналей. Сравните углы BQC и APD.
А. Ð BQC < Ð APD. Б. Ð BQC = Ð APD.
В. Ð BQC > Ð APD. Г. Сравнить нельзя.
15. Сторона D С параллелограмма ABCD разделена на 5 равных частей. Первая точка деления Р соединена с вершиной А. Прямая АР пересекает диагональ BD в точке Q. Отношение BD : DQ равно …
А. 4. Б. 5. В. 6. Г. числу, отличному от приведенных.
Повышенный уровень. Вариант 3.
1. Расположите в порядке убывания дроби 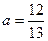 ,
, 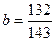 ,
, 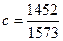 .
.
А . a = b = c. Б . a > b > c. В . c > b > a. Г . b > c > a.
2. Сравните 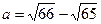 и b = 0,0625.
и b = 0,0625.
А. а > b. Б. а < b . В. a = b. Г. Без вычислительных средств сравнить нельзя.
3. Вычислите 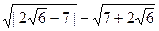 .
.
А. 2 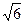 . Б. –2
. Б. –2 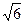 . В. 2. Г. –2.
. В. 2. Г. –2.
4. Укажите все значения x, при которых 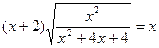 .
.
А. xÎ (–2; +¥). Б. xÎ(–¥; –2) È[0; +¥). В. xÎ (–2; 0]. Г. xÎ (–¥; 0].
5. Сколько корней имеет уравнение 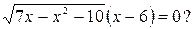
А. Ни одного. Б. Один. В. Два. Г. Три.
6. Уравнение ax2 + bx + c = 0 не имеет корней и a – b + c < 0. Какие знаки имеют числа а и с?
А. + +. Б. – +. В. + –. Г. – –.
7. Длина промежутка, состоящего из решений неравенства |а – 4x| < 3 равна …
А. 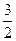 . Б.
. Б. 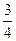 . В.
. В. 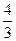 . Г.
. Г. 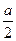 .
.
8.  Укажите все значения а, при которых график функции у = ах + 1 – а имеет вид, изображенный на рисунке.
Укажите все значения а, при которых график функции у = ах + 1 – а имеет вид, изображенный на рисунке.
А. Таких значений не существует. Б. a < 0. B . a > 1. Г. 0 < a < 1.
9. Множество решений уравнения x = x | y | изображено на рисунке …

10. Из 22 кг свежих грибов получается 2,5 кг сухих грибов, содержащих 12% воды. Процент воды в свежих грибах равен ...
А. 10%. Б. 20%. В. 80%. Г. 90%.
11. В треугольнике АВС сторона ВС равна 15 см. Через вершину А и точку, расположенную на медиане к стороне АС и делящую её в отношении 1:2, считая от вершины, проведена прямая до пересечения со стороной ВС в точке D. Отрезок CD равен ...
А. 9 см. Б. 6 см. В. 12 см. Г. 10 см.
12. Высоты треугольника АВС пересекаются в точке О. Известно, что ОС = АВ. Угол АСВ равен …
А. 30°. Б. 45°. В. 60°. Г. 75°.
13. Отрезки, соединяющие середины смежных сторон равнобедренной трапеции, образуют квадрат. Сравните среднюю линию трапеции d и её высоту h.
А. d < h. Б. d = h. В. d > h. Г. Сравнить нельзя.
14. Дан четырёхугольник, A, B, C, D — последовательные середины его сторон, P, Q — середины диагоналей. Сравните углы APB и CQD.
А. Ð APB < Ð CQD. Б. Ð APB = Ð CQD.
В. Ð APB > Ð CQD. Г. Сравнить нельзя.
15. Сторона СВ параллелограмма ABCD разделена на 4 равные части. Первая точка деления Р соединена с вершиной D. Прямая АР пересекает диагональ АС в точке Q. Отношение АС:С Q равно …
А. 5. Б. 4. В. 3. Г. числу, отличному от приведенных.
Подсказки к заданиям повышенного уровня
1. Постарайтесь найти закономерность образования числителей и знаменателей дробей b и с из числителя и знаменателя дроби а. Можно каждый числитель и каждый знаменатель дробей b и с представить в виде произведения двух множителей, один из которых общий для числителя и знаменателя.
2. Преобразуйте числовое выражение а к виду, удобному для его оценивания. Например, умножьте его и разделите на число, «сопряженное» данному выражению.
3. Представьте подкоренные выражения в виде квадратов двучленов и воспользуйтесь равенством: 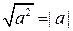 .
.
4. Воспользуйтесь дважды соотношением 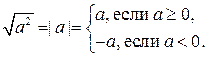
5. Воспользуйтесь тем, что множество решений уравнения вида f(x)g(x) = 0 является объединением множества решений систем 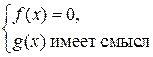 и
и 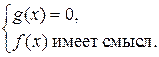 .
.
6. Установите, как расположен график квадратного трехчлена у = ах2 + bx + c и что представляет собой левая часть приведенного неравенства.
7. Решите заданное неравенство относительно х и воспользуйтесь тем, что длина искомого промежутка равна разности выражений, между которыми находится значение х.
8. Воспользуйтесь геометрическим смыслом параметров а и b линейной функции
у = ах + b.
9. Воспользуйтесь равенствами 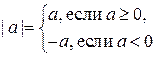 и геометрическим смыслом решений уравнения.
и геометрическим смыслом решений уравнения.
10. Воспользуйтесь правилами решения трёх основных задач на проценты: нахождение процента от числа, числа по его проценту и процентного отношения двух чисел. Определите массу вещества, рассматриваемого в задании, не содержащего воды.
11. Воспользуйтесь теоремой Фалеса или её обобщением.
Параллельные прямые, пересекающие стороны угла и отсекающие на одной из них равные отрезки, отсекают равные отрезки и на другой стороне.
Параллельные прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные отрезки.
Проведите прямую, параллельную проведенной в условии задания прямой.
12. Воспользуйтесь признаком равенства прямоугольных треугольников, свойством острых углов в прямоугольном треугольнике.
13. Установите перпендикулярность диагоналей трапеции.
14. Воспользуйтесь свойством средней линии треугольника и свойством углов с соответственно перпендикулярными сторонами.
Если стороны одного угла параллельны сторонам другого угла и если они оба острые или оба тупые, то они равны.
15. Воспользуйтесь теоремой Фалеса.
Параллельные прямые, пересекающие стороны угла и отсекающие на одной из них равные отрезки, отсекают равные отрезки и на другой стороне.
Углублённый уровень. Вариант 1
1. Укажите все значения, которые может принимать число x, если 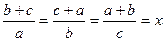 .
.
А. –1. Б. 0,5. В. –1; 0,5. Г. 2; –1.
2. Упростите выражение 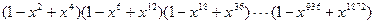 при х ¹ –1.
при х ¹ –1.
А. 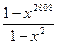 . Б.
. Б. 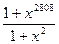 . В.
. В. 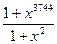 . Г.
. Г. 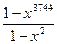 .
.
3. Сколько решений в целых числах имеет уравнение 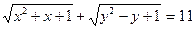 ?
?
А. 0. Б. 1. В. 2. Г. 3.
4. Тетрадь стоит 100 руб., ручка — 30 руб., а стержень к шариковой ручке — 5 руб. Ученик купил по крайней мере 1 тетрадь, 1 ручку и 1 стержень, всего 100 принадлежностей, израсходовав на покупку всего 1000 руб. Сколько стержней он купил?
А. 88. Б. 90. В. 92. Г. 94.
5. Сколько четырехзначных четных чисел с различными цифрами можно составить из цифр 0, 1, 2, 3, 4, 5?
А. 156. Б. 144. В. 300. Г. 200.
6. На кольцевой дороге проводилась эстафета мотоциклистов, которая состояла из 52 равных по длине этапов. Старт и финиш находились в одном месте. Длина кольцевой дороги 390 км. Какова минимально возможная длина одного этапа, если она составляет целое число километров?
А. 15 км. Б. 30 км. В. 45 км. Г. 60 км.
7. Девять одинаковых книг стоят 5600 рублей плюс небольшая сумма, меньшая 100 рублей, а 13 таких же книг стоят 8000 рублей плюс небольшая сумма, меньшая 100 рублей. Сколько стоит одна книга?
А. 616 руб. Б. 633 руб. В. 623 руб. Г. 629 руб.
8. Трава на всем лугу растет одинаково густо и быстро. Известно, что 35 коров съели бы ее за 40 дней, а 50 коров — за 25 дней. Сколько коров съели бы ее за 20 дней?
А. 60. Б. 64. В. 70. Г. 72.
9. Диагонали трапеции являются биссектрисами углов при меньшем основании, одна из боковых сторон равна 2 см. Периметр трапеции может равняться …
А. 9 см. Б. 7 см. В. 6 см. Г. 5 см.
10. В треугольнике АВС медиана АМ делит высоту ВН в отношении 3:1, считая от вершины В. В каком отношении данная высота делит данную медиану, считая от вершины А?
А. 1:2. Б. 1:3. В. 2:3. Г. 3:2.
Углубленный уровень. Вариант 2.
1. Укажите все значения, которые может принимать число x, если 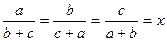 .
.
А. –1. Б. 0,5. В. –1; 0,5. Г. 2; –1.
2. Упростите выражение 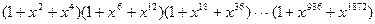 при х ¹ 1.
при х ¹ 1.
А. 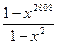 . Б.
. Б. 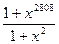 . В.
. В. 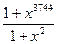 . Г.
. Г. 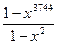 .
.
3. Сколько решений в целых числах имеет уравнение 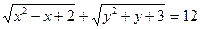 ?
?
А. 3. Б. 2. В. 1. Г. 0.
4.На 20 000 рублей закупили 100 птиц трёх видов. Индюшка стоит 2 000 руб., гусь — 600 руб., цыплёнок — 100 руб. Сколько было закуплено индюшек?
А. 3. Б. 4. В. 5. Г. 6.
5. Сколько четырехзначных чисел, делящихся на 4, с различными цифрами можно составить из цифр 0, 1, 2, 3, 4, 5?
А. 84. Б. 72. В. 36. Г. 63.
6. На кольцевой дороге проводилась эстафета мотоциклистов. Старт и финиш находились в одном и том же месте. Длина кольцевой дороги 390 км, а длина каждого этапа 45 км (движение одностороннее). Какое наименьшее число этапов могло быть в эстафете?
А. 26. Б. 13. В. 39. Г. 11.
7. Восемь одинаковых книг стоят 2600 рублей плюс небольшая сумма, меньшая 100 рублей, а 15 таких же книг стоят 4800 рублей плюс небольшая сумма, меньшая 100 рублей. Сколько стоит одна книга?
А. 321 руб. Б. 326 руб. В. 329 руб. Г. 332 руб.
8. Трава на всем лугу растет одинаково густо и быстро. Известно, что 70 коров съели бы ее за 40 дней, а 50 коров — за 64 дня. Сколько коров съели бы ее за 16 дней?
А. 100. Б. 150. В. 175. Г. 200.
9. Диагонали трапеции являются биссектрисами углов при большем основании, одна из боковых сторон равна 2 см. Периметр трапеции может равняться …
А. 6 см. Б. 7 см. В. 9 см. Г. 8 см.
10. В треугольнике АВС высота ВН делит медиану АМ в отношении 3:4, считая от вершины А. В каком отношении данная медиана делит данную высоту, считая от вершины В?
А. 4:3. Б. 8:3. В. 11:3. Г. 5:4.
Углубленный уровень. Вариант 3.
1. Укажите все значения, которые может принимать число x, если 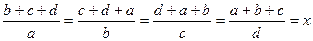
А. –1; 3. Б. 3. В. –1; –3. Г. 1; –3.
2. Упростите выражение 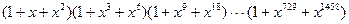 при х ¹ 1.
при х ¹ 1.
А. 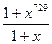 . Б.
. Б. 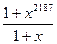 . В.
. В. 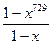 . Г.
. Г. 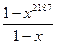 .
.
3. Сколько решений в целых числах имеет уравнение 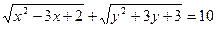 ?
?
А. 3. Б. 2. В. 1. Г. 0.
4. В комнате находятся люди, собаки и мухи — всего 10 особей. У человека 2 ноги, у собаки — 4, а у мухи 6 ног. У всех вместе 46 ног. Сколько имеется возможностей для такой ситуации?
А. Ни одной. Б. Одна. В. Две. Г. Три.
5. Сколько четырехзначных чисел, делящихся на 4, можно составить из цифр 0, 1, 2, 3, 4, 5 (цифры могут повторяться)?
А. 210. Б. 270. В. 324. Г. 252.
6. На кольцевой дороге проводилась эстафета мотоциклистов. Старт и финиш находились в одном и том же месте. Длина кольцевой дороги 330 км, а длина каждого этапа 75 км (движение одностороннее). Какое наименьшее число этапов могло быть в эстафете?
А. 22. Б. 11. В. 33. Г. 15.
7. Шесть одинаковых сувениров стоят 1700 рублей плюс небольшая сумма, меньшая 100 рублей, а 13 таких же сувениров стоят 3600 рублей плюс небольшая сумма, меньшая 100 рублей. Сколько стоит один сувенир?
А. 277 руб. Б. 278 руб. В. 282 руб. Г. 284 руб.
8. Трава на всем лугу растет одинаково густо и быстро. Известно, что 70 коров съели бы ее за 40 дней, а 50 коров — за 64 дня. За сколько дней съели бы ее 230 коров?
А. За 12. Б. За 10. В. За 9. Г. За 8.
9. Диагональ равнобедренной трапеции является биссектрисой её острого угла, меньшее основание равно 15 см. Периметр трапеции может равняться …
А. 50 см. Б. 55 см. В. 60 см. Г. 65 см.
10. Высота параллелограмма ABCD, проведенная из вершины тупого угла В к стороне AD, делит эту сторону в отношении 1:7, считая от вершины А. В каком отношении, считая от вершины А, эта высота делит диагональ АС?
А. 1:6. Б. 1:7. В. 1:8. Г. 2:7.
Подсказки к заданиям углубленного уровня
1. Выразите числители всех дробей через х и сложите левые и правые части полученных равенств.
2. Воспользуйтесь формулой суммы или разности кубов двух выражений.
3. Определив, четным или нечетным является произведение двух последовательностей целых чисел, установите четность или нечетность значений подкоренных выражений.
4. Составьте по условию систему уравнений и решите её в целых числах.
5. Установите, сколько вариантов есть для выбора каждой цифры указанного четырёхзначного числа с учётом возможного или невозможного повторения цифр.
6.Рассмотрите кратные длины кольцевой дороги.
7. Воспользуйтесь тем, что одна из указанных сумм должна превышать целое количество сотен рублей на сумму, численно не большую количества приобретенных на эту сумму предметов, а от второй до целого количество сотен рублей — не должно доставать суммы, тоже численно не превышающую количества соответствующих предметов.
8. Введите обозначения для массы травы, находящейся на лугу в начале рассматриваемого периода и для массы травы, вырастающей ежедневно, и выразите через них, исходя из условия, массу травы, поедаемой одной коровой за 1 день.
9. Воспользуйтесь определением биссектрисы и свойством параллельных прямых.
10. Воспользуйтесь теоремой Фалеса и её обобщением.
Параллельные прямые, пересекающие стороны угла и отсекающие на одной из них равные отрезки, отсекают равные отрезки и на другой стороне.
Параллельные прямые, пересекающие стороны угла, отсекают от сторон пропорциональные отрезки.
Ответы к тестам тренажёра
| Но-мер зада-ния | |||||
Вариант 1
Вариант 2
Вариант 3
| Уровень | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| Базовый | В | Б | В | А | В | Г | А | Г | В | Г | Б | А | В |
| Основной | А | В | Б | Г | Б | В | В | Г | В | А | В | Г | А |
| Продвинутый | Г | А | В | Г | Б | Г | А | Б | В | Г | Г | А | В |
| Повышенный | А | Б | Г | Б | В | Г | А | Г | В | Г | В | Б | А |
| Углублённый | А | В | Г | Б | Б | Б | Г | В | Г | В | |||
| 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | ||
| Базовый | Б | Г | В | Б | А | А | В | Г | Б | В | Б | А | |
| Основной | В | Б | В | Г | Г | Г | В | В | Б | Г | Г | Г | |
| Продвинутый | А | Г | Б | Б | Б | Г | Б | ||||||
| Повышенный | Б | А | |||||||||||
Контрольное задание
Контрольное задание состоит из основного и дополнительного заданий, которые оцениваются отдельно. Основное задание предполагает выполнение тестов базового, основного и продвинутого уровней. Дополнительное – тестов повышенного и углублённого уровней. Вы выбираете правильные ответы ко всем заданиям и пересылаете их тьютору.
Каждый правильный ответ на задание базового уровня оценивается одним баллом, основного – двумя баллами, продвинутого – четырьмя баллами, повышенного – шестью баллами и углубленного – десятью баллами.
Критерии оценок
Основное задание :
«отлично» - получено от 121 до 155 баллов
«хорошо» - получено от 91 до 120 баллов
«зачтено» - получено от 52 до 90 баллов
Дополнительное задание:
«отлично» - получено от 81 до 190 баллов
«хорошо» - получено от 54 до 80 баллов
Срок выполнения задания – 4 недели.
Надеемся, что работа над тестами будет для Вас и интересной, и полезной.
Желаем Вам успехов!
Основное задание
Базовый уровень
1. Вычислите: 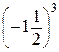 .
.
А. 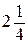 . Б.
. Б. 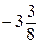 . В.
. В. 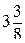 . Г. –
. Г. – 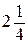 .
.
2. Вычислите значение выражения 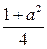 при а = –
при а = – 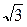 .
.
А. 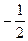 . Б.
. Б. 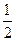 . В. 1. Г.
. В. 1. Г. 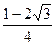 .
.
3. Вычислите значение выражения 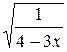 при х = –15.
при х = –15.
А. 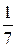 . Б.
. Б. 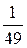 . В. ±
. В. ± 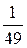 . Г.
. Г. 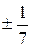 .
.
4. Между какими последовательными целыми числами находится число 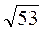 ?
?
А. 6 и 7. Б. 7 и 8. В. 8 и 9. Г. 5 и 6.
5. Сравните числа а = –5,137 и b = –5,317.
А. a < b. Б. а = b. В. а > b. Г. Нельзя сравнить.
6. Упростите выражение 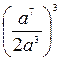 .
.
А. 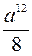 . Б.
. Б. 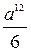 . В.
. В. 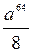 . Г.
. Г. 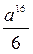 .
.
7. Упростите выражение 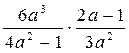 .
.
А. 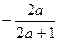 . Б.
. Б. 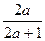 . В.
. В. 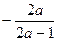 . Г.
. Г. 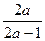 .
.
8. Укажите все значения х, при которых имеет смысл выражение 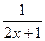 .
.
А. х < – 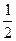 . Б. x > –
. Б. x > – 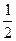 . В. х ¹ –
. В. х ¹ – 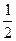 . Г. х ¹
. Г. х ¹ 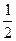 .
.
9. Из формулы 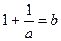 выразите a через b.
выразите a через b.
А. а = 1 – b. Б. a = b – 1. В. 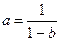 . Г.
. Г. 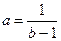 .
.
10. Корнями уравнения (х + 1)(х – 3) = 0 являются числа …
А. 1 и –3. Б. –1 и 3. В. 1 и 3. Г. –1 и –3.
11. Сравните числа х и у, если х – у = (–1)5.
А. х > у. Б. х = у. В. х < у. Г. х ³ у.
12. График функции 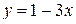 проходит через точку …
проходит через точку …
 А. (2; –5). Б.
А. (2; –5). Б. 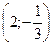 . В. (2; 5) Г.
. В. (2; 5) Г. 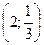 .
.
13. На рисунке изображен график функции …
А . y = x + 2. Б . y = –x + 2. В . y = –x – 2. Г . y = x – 2.
14. На рисунке представлен график движения пешехода из пункта А в пункт В, где s – расстояние от пешехода до пункта В, t — время движения. Сколько километров пройдено пешеходом после привала?
 А. 20 км. Б. 10 км. В. 1 км. Г. 2 км.
А. 20 км. Б. 10 км. В. 1 км. Г. 2 км.
15. При выполнении работы по математике 12% учащихся класса совсем не решили задачи, 32% решили с ошибками, остальные 14 человек решили верно. Сколько учеников было в классе?
А. 32. Б. 24. В. 25. Г. 20.
16. Какая из точек А(5; –2), В(–2; 3), С(–1; 4), D(2; 1) расположена ближе всего к оси у?
А. С. Б. В. В. А. Г. D.
17. Через точку А(3; –2) проведена прямая, параллельная оси х. Точка ее пересечения с осью у имеет координаты …
А.(0; 3). Б.(3; 0). В. (–2; 0). Г. (0; –2).
18. В равнобедренном треугольнике основание и боковая сторона соответственно равны 12 см и 10 см. Высота, опущенная на его основание, равна …
А. 6 см. Б. 13 см. В. 3 см. Г. 8 см.
19. Из точки А, взятой вне прямой, проведены к этой прямой перпендикуляр АВ и наклонная АС. Наклонная образует с этой прямой угол 37°. Сравните длины перпендикуляра АВ и проекции наклонной ВС.
А. A В = BC. Б. АВ < BC. В. A В > B C. Г. Сравнить нельзя.
20. Углы равнобедренной трапеции не могут быть равными ...
А. 35° и 145°. Б. 40° и 140°. В. 120° и 150°. Г. 75° и 105°.
21. . В прямоугольнике угол между диагональю и большей стороной равен 30о. Диагональ равна 14 см. Меньшая сторона прямоугольника равна …
А. 7 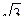 см. Б. 7 см. В. 14
см. Б. 7 см. В. 14 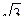 см. Г. 28 см.
см. Г. 28 см.
22. Середина одной из сторон четырехугольника соединена с серединами других сторон. Сколько при этом получилось отрезков?
А. 4. Б. 2. В. 3. Г. Ответ отличен от приведенных.
23. Радиус окружности равен 6 см. Диагональ квадрата, вписанного в окружность, равна …
А. 6 см. Б. 6 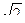 см. В. 12
см. В. 12 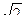 см. Г. 12 см.
см. Г. 12 см.
24. Как изменится площадь треугольника, если его стороны увеличить вдвое?
А. Увеличится в 4 раза. Б. Увеличится в 3 раза.
В. Увеличится в 2 раза. Г. Не изменится.
25. В круге диаметром 10 см проведена хорда, удаленная от центра на 3 см. Длина хорды равна ...
А. 4 см. Б. 8 см. В. 12 см. Г. Величине, отличной от приведенных.
Основной уровень.
1. Вычислите 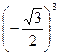 .
.
А. 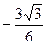 . Б.
. Б. 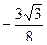 . В.
. В. 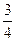 . Г.
. Г. 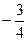 .
.
2. Вычислите значение выражения 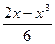 при x =
при x = 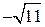 .
.  .
.
А. 3 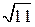 . Б.
. Б. 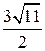 . В. –3
. В. –3 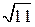 . Г. –
. Г. – 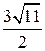 .
.
3. Найдите значение выражения 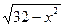 при
при 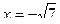 .
.
А. –5. Б. ± 5. В. 5. Г. Выражение не имеет смысла.
4. Расположите в порядке возрастания числа 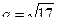 ,
, 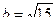 , с = 4.
, с = 4.
А . b < c < a. Б . b < a < c. В . c < b < a. Г. c < a < b.
5. Сравните числа 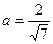 и
и 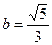 .
.
А. a = b. Б. a < b. В. a > b. Г. Сравнить нельзя.
6. Упростите выражение 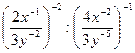 .
.
А. 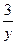 . Б.
. Б. 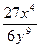 . В.
. В. 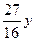 . Г.
. Г. 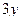 .
.
7. Упростите выражение 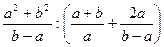 .
.
А. –a. Б. a. В. 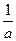 . Г. –
. Г. – 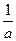 .
.
8. Укажите все значения x, при которых выражение 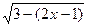 не имеет смысла?
не имеет смысла?
А. 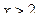 . Б.
. Б. 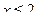 . В.
. В. 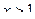 . Г.
. Г. 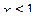 .
.
9. Из формулы 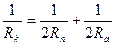 , дающей соотношение между радиусом кривизны орбиты и расстояниями перигея и апогея от центра Земли, выразите R к через R а и Rn.
, дающей соотношение между радиусом кривизны орбиты и расстояниями перигея и апогея от центра Земли, выразите R к через R а и Rn.
А. 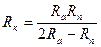 . Б.
. Б. 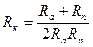 . В.
. В. 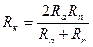 . Г.
. Г. 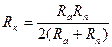 .
.
10. Один из корней уравнения 3x2 + 7x + 2 = 0 равен –2. Второй его корень равен …
 А. –
А. – 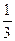 . Б.
. Б. 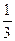 . В. –
. В. – 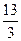 . Г.
. Г. 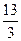 .
.
11. Сравните числа а и b, если разность a – b представляет собой куб отрицательного числа.
А. a = b. Б. a < b. В. a > b. Г. Сравнить нельзя.
12. На рисунке изображен график функции y = 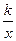 . Коэффициент k равен …
. Коэффициент k равен …
А. –2. Б. 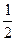 . В. –
. В. – 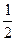 . Г. 2.
. Г. 2.
13. Какой из следующих графиков может быть графиком функции  ?
?


14. На рисунке дан график зависимости ускорения а движущегося тела от его массы m при постоянной силе F, действующей на это тело (F = ma). Для какой массы ускорение превосходит 1,5 м/с2?
А. m = 20 кг. Б. m < 20 кг.
В. m > 20 кг. Г. Определить нельзя.
15. В каком отношении нужно смешать два вида фруктового сока с концентрацией сахара 15% и 20%, чтобы концентрация сахара в их смеси равнялась 18%?
А. 1:4. Б. 2:3. В. 3:5. Г. 3:2.
16.  Какая из приведенных точек находится на том же расстоянии от прямой x = –1, что и точка (2; –3)?
Какая из приведенных точек находится на том же расстоянии от прямой x = –1, что и точка (2; –3)?
А.( –4; –3). Б.(2; 1). В.( –4; 1). Г.( –1; –3).
17. На рисунке АВCD — параллелограмм, AD = 15 см, CE = 2 см, CF = 3 см. Длина стороны AB равна ...
А. 6 см. Б. 9 см. В. 10 см. Г. 8 см.
18. Диагональ прямоугольника равна 15 см, расстояние от точки пересечения диагоналей до большей его стороны равно 4,5 см.Чему равна большая сторона прямоугольника?
А. 9 см. Б. 10 см. В. 12 см. Г. 18 см.
19. Из вершины С тупого угла прямоугольной трапеции АВС D проведён перпендикуляр С F на основание AD, ÐBCD = 135°. Сравните отрезки CF и DF.
А . CF = DF. Б . CF < DF. В. CF > DF. Г. Сравнить нельзя.
20. Какую фигуру образуют прямые, последовательно соединяющие середины сторон ромба?
А. Прямоугольник. Б. Квадрат. В. Ромб. Г. Трапецию.
21. В равнобедренной трапеции тупой угол равен 120°, боковая сторона равна 12 см, а большее основание 18 см. Средняя линия и высота трапеции соответственно равны …
А. 12 см и 3 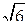 см. Б. 14 и 4
см. Б. 14 и 4 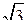 см. В. 14 см и 6
см. В. 14 см и 6 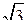 см. Г. 9 см и 3
см. Г. 9 см и 3 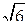 см.
см.
22. Три луча, выходящие из одной точки, пересечены двумя параллельными прямыми. Сколько при этом получилось трапеций?
А. 6. Б. 4. В. 3. Г. 2
23. Четырёхугольник ABCD — трапеция (ВС ½½ AD), ВС > AD, АС — ее диагональ, MN — средняя линия, M Î AB, N Î CD, K — точка пересечения AC и MN. Сравните отрезки M K и N K.
А. MK = NK. Б. MK < NK. В. MK > NK. Г. Сравнить нельзя.
24.  В параллелограмме ABCD B M:M C = 2:3. Площади треугольника AB M и четырехугольника AМCD относятся как...
В параллелограмме ABCD B M:M C = 2:3. Площади треугольника AB M и четырехугольника AМCD относятся как...
А. 1:3. Б. 1:4. В. 1:5. Г. 2:3.
25. В равнобедренной трапеции основания равны 7 см и 17 см, а диагональ равна 13 см. Площадь трапеции равна ...
А. 120 см2. Б. 90 см2. В. 75 см2. Г. 60 см2.
Продвинутый уровень
1. О натуральных числах c и d известно, что c > d. Расположите в порядке убывания числа x = 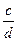 , y =
, y = 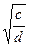 , z =
, z = 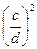 .
.
А. z > x > y. Б. z > y > x. В. y > x > z. Г. y > z > x.
2. Упростите выражение 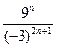 .
.
А. –3. Б. 3. В. – 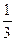 . Г.
. Г. 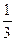 .
.
3. Сравните числа  и
и 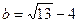 .
.
А. Сравнить нельзя. Б. a = b. В. a < b. Г. a > b.
4. Чему равно выражение 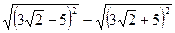 ?
?
А. –10. Б. 10. В. 6 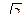 . Г. –6
. Г. –6 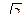 .
.
5. Укажите наименьшее целое число x, при котором справедливо равенство
|–x – 2| = 2 + x.
А. 2. Б. –2. В. 0. Г. Такого числа не существует.
6. Уравнение x2 + px + q = 0 не имеет корней. Сколько корней будет иметь уравнение, полученное из данного уменьшением его свободного члена?
А. 0. Б. 1. В. 2. Г. Однозначного ответа нет.
7. Квадратное уравнение а x2 – x – с = 0 имеет корень, равный 2, если …
А. 4а – c = –2. Б. 4а – c = 2. В. 4а = – c + 2. Г. 4а – c = 0.
8. Укажите все значения b и с, при которых квадратный трехчлен а x2 + bx + 3 имеет противоположные корни.
А. b = 0, а > 0. Б. b = 0, а < 0. В. а < 0, b — любое. Г. b ¹ 0, а — любое.
9. Сколько общих точек имеют графики функций 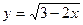 и y = x?
и y = x?
А. Ни одной. Б. Одну. В. Две. Г. Три.
10. График функции y = 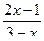 не имеет общих точек с прямой …
не имеет общих точек с прямой …
А. y = –2. Б. y = 2. В. x = 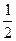 . Г. x = –3.
. Г. x = –3.
11.  На рисунке дан график зависимости между сторонами прямоугольника постоянной площади. Площадь прямоугольника равна …
На рисунке дан график зависимости между сторонами прямоугольника постоянной площади. Площадь прямоугольника равна …
А. 4 м2. Б. 6 м2. В. 8 м2. Г. 10 м2.
12. Цена на некоторый продукт уменьшилась на 20%. Было решено сохранить затраты на покупку этого продукта. На сколько процентов увеличится потребление данного продукта?
А. На 20%. Б. На 25%. В. На 16 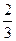 %. Г. На 26
%. Г. На 26 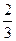 % .
% .
13. Какой вид имеет треугольник, отсекаемый биссектрисой острого угла параллелограмма?
А. Прямоугольный. Б. Остроугольный.
 В. Равнобедренный. Г. Разносторонний.
В. Равнобедренный. Г. Разносторонний.
14. Через точку пересечения диагоналей параллелограмма проведены две прямые. Точки пересечения этих прямых со сторонами параллелограмма последовательно соединены. Полученный четырехугольник является …
 А. трапецией. Б. ромбом.
А. трапецией. Б. ромбом.
В. прямоугольником. Г. параллелограммом.
15. В прямоугольном треугольнике через произвольную точку гипотенузы проведены две прямые, параллельные катетам. Сумма периметров полученных двух треугольников равна 12 см. Периметр данного треугольника равен…
А. 6 см. Б. 12 см. В. 18 см. Г. 24 см.
16. Высота равностороннего треугольника равна h. Его сторона равна …
А. 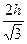 . Б.
. Б. 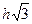 . В.
. В. 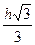 . Г.
. Г. 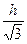 .
.
17. Биссектриса угла А прямоугольника ABCD делит сторону BC в отношении 1:2, считая от вершины, а периметр его равен 40 см. Стороны прямоугольника равны …
А. По 10 см. Б. 5 и 15 см. В. 8 и 12 см. Г. 4 и 16 см.
18. Две медианы треугольника взаимно перпендикулярны, равны m1 и m2. Площадь треугольника равна …
 А. m1m2. Б.
А. m1m2. Б. 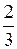 m1m2. В.
m1m2. В. 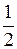 m1m2. Г.
m1m2. Г. 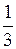 m1m2.
m1m2.
19. Если АВСD — трапеция (АD||ВС), ÐBАС = ÐCDА, BC = 2, АD = 8, то диагональ АС равна …
А. 5. Б. 4. В. 3. Г. 6.
20. Совокупность точек плоскости, удаленных от данной точки на одно и то же расстояние, образует …
А. прямую. Б. две прямые. В. окружность. Г. полосу.
Дополнительное задание
Повышенный уровень
1. Расположите дроби в порядке возрастания 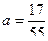 ,
, 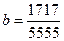 ,
, 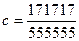 .
.
А . a = b = c. Б . a < b < c. В . c < b < a. Г . b < c < a.
2. Сравните 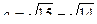 и b = 0,125.
и b = 0,125.
А. а > b. Б. а < b . В. a = b. Г. Без вычислительных средств сравнить нельзя.
3. Вычислите 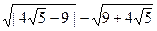 .
.
А. 2 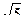 . Б. –2
. Б. –2 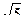 . В. 4. Г. –4.
. В. 4. Г. –4.
4. Укажите все значения x, при которых справедливо равенство 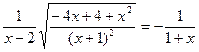 .
.
А.(–¥; –1). Б.(2; +¥). В.(–¥; –1)È(2; + ¥). Г.(–1; 2).
5. Сколько корней имеет уравнение 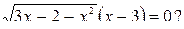
А. Четыре. Б. Три. В. Два. Г. Один.
6. Уравнение ax2 + bx + c = 0 не имеет корней и a – b + c > 0. Какие знаки имеют числа а и с?
А. + +. Б. – +. В. + –. Г. – –.
7. Длина промежутка, состоящего из решений неравенства | 4x – 3| < а равна …
 А.
А. 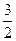 . Б.
. Б. 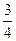 . В.
. В. 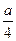 . Г.
. Г. 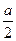 .
.
8. Укажите все значения а, при которых график функции у = ах + 1 – а имеет вид, изображенный на рисунке.
А. Таких значений не существует. Б. a < 0. B . a > 1. Г. 0 < a < 1.
9. Множество решений уравнения y = y | x | изображено на рисунке …

10. На овощной базе хранились огурцы, содержащие 99% воды по весу. За время хранения часть воды испарилась, в результате чего в огурцах стало 98% воды. Сколько процентов своего веса потеряли огурцы?
А. 1% . Б. 50%. В. 2%. Г. 20%.
11. В треугольнике АВС сторона ВС равна 15 см. Через вершину А и точку, расположенную на медиане к стороне АС и делящую её в отношении 1:2, считая от вершины, проведена прямая до пересечения со стороной ВС в точке D. Отрезок В D равен ...
А. 3 см. Б. 6 см. В. 9 см. Г. 4,5 см.
12. Высоты треугольника АВС пересекаются в точке О, BD ^ AC, D Î AC. Известно, что ОА = ВС. Угол DO С равен …
А. 30°. Б. 45°. В. 60°. Г. 75°.
13. Средняя линия равнобедренной трапеции равна её высоте. Какую фигуру образуют отрезки, соединяющие середины её смежных сторон?
А. Трапецию. Б. Ромб, не являющийся квадратом.
В. Прямоугольник, не являющийся квадратом. Г. Квадрат.
14. Дан четырёхугольник, A, B, C, D — последовательные середины его сторон, P, Q — середины диагоналей. Сравните углы AQB и CPD.
А. Ð AQB < Ð CPD. Б. Ð AQB = Ð CPD.
В. Ð AQB > Ð CPD. Г. Сравнить нельзя.
15. Сторона АВ параллелограмма ABCD разделена на 4 равные части. Первая точка деления Р соединена с вершиной D. Прямая D Р пересекает диагональ АС в точке Q. Отношение АС:А Q равно …
А. 5. Б. 4. В. 3. Г. числу, отличному от приведенных.
Углублённый уровень
1. Укажите все значения, которые может принимать число x, если 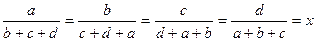
А. –1. Б. 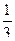 . В. –1;
. В. –1; 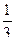 . Г. 1; –
. Г. 1; – 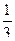 .
.
2. Упростите выражение 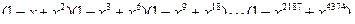 при х ¹ –1.
при х ¹ –1.
А. 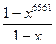 . Б.
. Б. 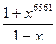 . В.
. В. 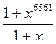 . Г.
. Г. 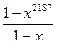 .
.
3. Сколько решений в целых числах имеет уравнение 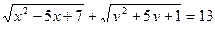 ?
?
А. 0. Б. 1. В. 2. Г. 3.
4. Летит стая сороконожек и трехглавых драконов. У всех у них 26 голов и 298 ног. У каждой сороконожки одна голова. Сколько ног у трехглавого дракона?
А. 7. Б. 5. В. 14. Г. 21.
5. Даны 6 цифр: 0, 1, 2, 3, 4, 5. Сколько четырехзначных нечетных чисел с разными цифрами можно записать этими цифрами?
А. 156. Б.300. В. 108. Г. 144.
6. На кольцевой дороге проводилась эстафета мотоциклистов, которая состояла из 44 равных по длине этапов. Старт и финиш находились в одном месте. Длина кольцевой дороги 330 км. Какова минимально возможная длина одного этапа, если она составляет целое число километров?
А. 15 км. Б. 30 км. В. 45 км. Г. 60 км.
7. Семь одинаковых сувениров стоят 4300 рублей плюс небольшая сумма, меньшая 100 рублей, а 18 таких же сувениров стоят 11300 рублей плюс небольшая сумма, меньшая 100 рублей. Сколько стоит один сувенир?
А. 626 руб. Б. 628 руб. В. 631 руб. Г. 634 руб.
8. Трава на всем лугу растет одинаково густо и быстро. Известно, что 35 коров съели бы ее за 40 дней, а 50 коров – за 25 дней. За сколько дней съели бы ее 60 коров?
А. За 16. Б. За 18. В. За 20. Г. За 21.
9. Диагональ равнобедренной трапеции является биссектрисой её тупого угла, большее основание равно 15 см. Периметр трапеции может равняться …
А. 70 см. Б. 65 см. В. 60 см. Г. 55 см.
10. Высота параллелограмма ABCD, проведенная из вершины тупого угла В к стороне AD, делит диагональ АС в отношении 1:6, считая от вершины А. В каком отношении, считая от вершины А, эта высота делит сторону AD?
А. 1:5. Б. 1:6. В. 1:7. Г. 2:5.
Содержание
Повторим математику. 4
Зачем нужно повторять математику?. 4
Как можно повторить математику?. 4
Как организовать повторение. 5
Организация тренировок. 5
Тренажёр.. 6
Базовый уровень Вариант 1. 6
Базовый уровень Вариант 2. 8
Базовый уровень. Вариант 3. 10
Подсказки к заданиям базового уровня. 12
Основной уровень Вариант 1. 16
Основной уровень Вариант 2. 18
Основной уровень. Вариант 3. 20
Подсказки к заданиям основного уровня. 22
Продвинутый уровень Вариант 1. 27
Продвинутый уровень. Вариант 2. 28
Продвинутый уровень. Вариант 3. 30
Подсказки к заданиям продвинутого уровня. 32
Повышенный уровень. Вариант 1. 35
Повышенный уровень. Вариант 2. 36
Повышенный уровень. Вариант 3. 37
Подсказки к заданиям повышенного уровня. 38
Углублённый уровень. Вариант 1. 40
Углубленный уровень. Вариант 2. 40
Углубленный уровень. Вариант 3. 41
Подсказки к заданиям углубленного уровня. 42
Ответы к тестам тренажёра. 43
Контрольное задание. 44
Основное задание. 45
Базовый уровень. 45
Основной уровень. 47
Продвинутый уровень. 49
Дополнительное задание. 51
Повышенный уровень. 51
Углублённый уровень. 52
Центр математического просвещения
Я.С. Бродский, А.Л. Павлов
ПОВТОРИМ МАТЕМАТИКУ
8 – 9 классы

Донецк 2018
ББК 22.1я 72
Б88
Дата: 2018-11-18, просмотров: 1161.