Самый простой способ повторения состоит в листании учебника или справочника по математике. Простой, но бесполезный.
Настоящее повторение состоит в осознании того, что из знаний и умений осталось, а что потерялось. А это можно проверить, только что-то делая. Поэтому настоящее повторение предполагает выполнение разнообразных заданий, подобных тем, которые выполнялись ранее, но таких, что выявляют пробелы. Кроме того, необходимы анализ допущенных ошибок и их устранение.
Именно такое повторение предполагает настоящее пособие. Оно предусматривает:
- выполнение заданий разного уровня сложности, охватывающих главное содержание изученной математики;
- анализ результатов выполнения заданий и корректировку математической подготовки;
- установление уровня готовности к дальнейшему обучению математике.
В данном пособии выполнение заданий сводится к выбору правильного ответа из приведенных. Для повторения большого массива материала такие задания вполне пригодны. Среди заданий есть и очень сложные.
Пособие состоит из двух частей. Первая часть предназначена для тренировки. Поэтому она называется «Тренажёром». Вторая часть предназначена для проверки того, эффективны ли были тренировки. Поэтому она называется «контрольным заданием».
Как организовать повторение
Организация повторения состоит из организации тренировок и организации работы над контрольным заданием.
Организация тренировок
1. Надо сначала попробовать выполнить самостоятельно задания первого варианта теста базового уровня, содержащегося в тренажёре. Выбранные ответы записывайте на отдельном листочке.
Пользоваться учебником и калькулятором не рекомендуется. Желательно это сделать за 40 – 50 минут.
2. После завершения работы над первым вариантом теста необходимо сверить свои ответы с приведенными в пособии.
Нельзя обращаться к приведенным ответам, пока не получены самостоятельно ответы ко всем заданиям.
3.
Каждое задание, по которому ответ не совпал с приведенным, нужно тщательно проанализировать, пользуясь при необходимости приведенными в пособии указаниями.
Такую работу полезно проделать со всеми заданиями теста. Наверное, некоторые ответы угаданы или «почувствованы».
4. Когда появится уверенность в том, что неясных вопросов не осталось, можно проверить надёжность своей уверенности с помощью второго варианта теста базового уровня.
Если до конца выполнены данные выше рекомендации, то результаты при повторном тестировании будут значительно выше первоначальных.
5. Если уверенность подтвердилась при выполнении второго варианта теста, то можно подняться на ступеньку выше — перейти к работе над первым вариантом теста основного уровня. Методика работы над ним остаётся такой же.
6. Если же при выполнении второго варианта теста базового уровня осталось ощущение, что не всё усвоено, то нужно продолжать работу по исправлению ошибок, ещё раз выполнить задания второго варианта, записывая при этом все проделанные шаги. Дальнейшее движение по тренажёру проводится по той же схеме. Оно зависит от возможностей и от желаний.
Ни в коем случае не бросайте работу!
Постарайтесь пройти все этапы тренировок!
Тренажёр
Базовый уровень Вариант 1
1. Вычислите: 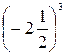 .
.
А. 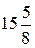 . Б. –
. Б. – 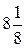 . В.
. В. 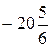 . Г.
. Г. 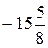 .
.
2. Вычислите значение выражения 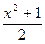 при
при 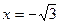 .
.
А. –1. Б. 2. В. 1. Г. –2.
3. Вычислите значение выражения 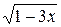 при х = –5.
при х = –5.
А. ±4. Б. 16. В. 4. Г. ±16.
4. Между какими последовательными натуральными числами заключено число 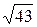 ?
?
А. 6 и 7. Б. 5 и 6. В. 7 и 8. Г. 4 и 5.
5. Сравните числа 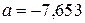 и b = – 7,563.
и b = – 7,563.
А . a = b. Б . a < b. В . a > b. Г . Сравнить нельзя.
6. Упростите выражение 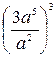 .
.
А. 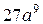 . Б.
. Б. 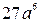 . В.
. В. 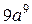 . Г.
. Г. 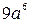 .
.
7. Упростите выражение 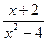 .
.
А. х – 2. Б. 2 – х. В. 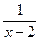 . Г.
. Г. 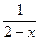 .
.
8. Укажите все значения х, при которых имеет смысл выражение 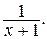
А. 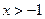 . Б.
. Б. 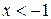 . В.
. В. 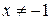 . Г.
. Г. 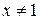 .
.
9. Из формулы 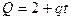 выразите переменную t.
выразите переменную t.
А. 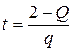 . Б.
. Б. 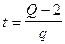 . В.
. В. 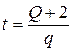 . Г.
. Г. 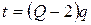 .
.
10. Корнями уравнения (х + 5)x = 0 являются числа …
А. 0 и –5. Б. 0 и 5. В. 1 и –5. Г. 1 и 5.
11. Сравните числа а и b, если а – b = 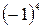 .
.
А . а < b. Б . a = b. В . a > b. Г . 
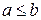 .
.
12. График функции y = 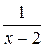 проходит через точку ¼
проходит через точку ¼
А. (1; 1). Б. 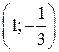 . В.
. В. 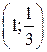 . Г. (1; –1).
. Г. (1; –1).
13. 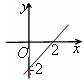 На рисунке изображен график функции …
На рисунке изображен график функции …
А . y = x + 2. Б . y = –x + 2. В . y = x – 2. Г . y = –x – 2.
14. 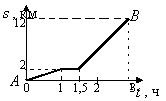 На рисунке представлен график прямолинейного движения туриста из пункта А в пункт В, где s — расстояние туриста до пункта А, t — время движения. Сколько времени двигался турист до привала?
На рисунке представлен график прямолинейного движения туриста из пункта А в пункт В, где s — расстояние туриста до пункта А, t — время движения. Сколько времени двигался турист до привала?
А. 2 ч. Б. 3 ч. В. 1,5 ч. Г. 1 ч.
15. В классе 10 % учащихся занимаются только легкой атлетикой, 50 % — только гимнастикой, а остальные 12 учеников —только игровыми видами спорта. Сколько учащихся в классе?
А. 35. Б. 30. В. 25. Г. 28.
16. Какая из точек E(–1; 2), F(2; –1), G(2; –3), H(4; 6) расположена ближе всего к оси х?
А. F. Б. E. В. G. Г. H.
17. Через точку А(–1; 4) проведена прямая, параллельная оси у. Точка ее пересечения с осью х имеет координаты …
А. (0; 4). Б. (4; 0). В. (0; –1). Г. (–1; 0).
18. Из одной точки, лежащей вне прямой, проведены к этой прямой перпендикуляр длиной 6 см и наклонная длиной 10 см. Длина ее проекции на прямую равняется …
А. 4 см. Б. 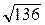 см. В. 8 см. Г. величине, отличной от приведенных.
см. В. 8 см. Г. величине, отличной от приведенных.
19. В прямоугольном треугольнике АВС длины катетов АС и ВС равны соответственно 5 см и 7 см. Сравните острые углы А и В.
А. ÐA < ÐB. Б. ÐA = ÐB. В. ÐA > ÐB. Г. Сравнить нельзя.
20. Углы параллелограмма могут равняться ...
А. 35° и 145°. Б. 50° и 40°. В. 120° и 150°. Г. 75° и 115°.
21. В прямоугольном треугольнике один из углов равняется 60°, а катет, прилежащий к нему, равен 12 см. Гипотенуза равна ....
А. 12 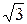 см . Б. 18 см. В. 18
см . Б. 18 см. В. 18 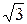 см. Г. 24 см.
см. Г. 24 см.
22. Сколько диагоналей можно провести из одной вершины шестиугольника?
А. 6. Б. 5. В. 4. Г. 3.
23. Из точки, лежащей вне круга, проведены к окружности, ограничивающей этот круг, две взаимно перпендикулярные касательные. Радиус круга равен 10 см. Длина каждой касательной равна …
А. 10 см. Б. 5 см. В. 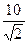 см. Г. величине, отличной от приведенных.
см. Г. величине, отличной от приведенных.
24. Как изменится площадь прямоугольника, если одну сторону увеличить вдвое, а другую — уменьшить вдвое?
А. Увеличится в 2 раза. Б. Уменьшится в 2 раза.
В. Увеличится в 1,5 раза. Г. Не изменится.
25. В круге проведена хорда длиной 8 см, удаленная от центра на 3 см. Диаметр круга равен ...
А. 5 см. Б. 12 см. В. 10 см. Г. величине, отличной от приведенных.
Базовый уровень Вариант 2
1. Вычислите: 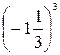 .
.
А. 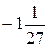 . Б.
. Б. 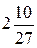 . В.
. В. 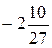 . Г.
. Г. 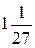 .
.
2. Вычислите значение выражения 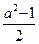 при
при 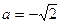 .
.
А. 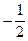 . Б.
. Б. 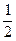 . В.
. В. 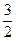 . Г.
. Г. 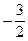 .
.
3. Вычислите значение выражения 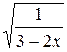 при х = –11.
при х = –11.
А. ± 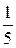 . Б.
. Б. 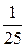 . В. ±
. В. ± 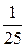 . Г.
. Г. 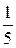 .
.
4. Между какими последовательными натуральными числами расположено число 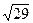 ?
?
А. 5 и 6. Б. 6 и 7. В. 4 и 5. Г. 7 и 8.
5. Сравните числа 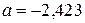 и
и 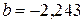 .
.
А . a = b. Б . a < b. В . a > b. Г . Сравнить нельзя.
6. Упростите выражение 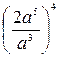 .
.
А. 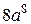 . Б.
. Б. 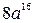 . В.
. В. 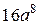 . Г.
. Г. 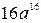 .
.
7. Упростите выражение 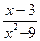 .
.
А. 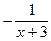 . Б.
. Б. 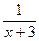 . В.
. В. 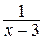 . Г.
. Г. 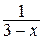 .
.
8. Укажите все значения х, при которых имеет смысл выражение 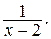
А. 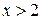 . Б.
. Б. 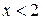 . В.
. В. 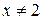 . Г.
. Г. 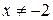 .
.
9. Из формулы 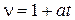 выразите переменную
выразите переменную 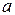 .
.
А. 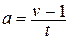 . Б.
. Б. 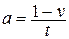 . В.
. В. 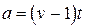 . Г.
. Г. 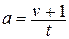 .
.
10. Найдите корни уравнения 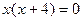 .
.
А. 0 и 4. Б. 1 и 4. В. 0 и – 4. Г. 1 и – 4.
11. Сравните числа а и b, если а – b = (–1)5 .
А . а > b. Б . a = b. В . a ³ b. Г . b > a.
12. График функции y = 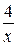 проходит через точку…
проходит через точку…
 А. (–2; 2). Б. (–2; –2). В.
А. (–2; 2). Б. (–2; –2). В. 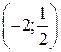 . Г.
. Г. 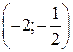 .
.
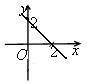
13. На рисунке изображен график функции …
А. 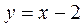 . Б.
. Б. 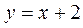 . В. .
. В. . 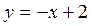 . Г.
. Г. 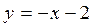 .
.
14. 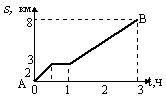 На рисунке представлен график движения туриста из пункта А в пункт В, где s — расстояние от туриста до пункта А, t — время движения. Сколько километров прошел турист после привала?
На рисунке представлен график движения туриста из пункта А в пункт В, где s — расстояние от туриста до пункта А, t — время движения. Сколько километров прошел турист после привала?
А. 5 км. Б. 4 км. В. 3 км. Г. 8 км.
15. В классе 20 % учащихся изучают только английский язык, 30 % — только французский, а остальные 15 учащихся — только немецкий. Сколько учащихся в классе?
А. 25. Б. 24. В. 35. Г. 30.
16. Какая из точек М(2; –1), N(–1; 2), P(0; 3), Q(1; –4) расположена дальше всех от оси у?
А. Q. Б. M. В. P. Г. N.
17. Через точку А(2; –3) проведена прямая, параллельная оси х. Точка ее пересечения с осью у имеет координаты …
А. (0; –3). Б. (2; 0). В. (0; 2). Г. (–3; 0).
18. Из одной точки, расположенной вне прямой, проведены к этой прямой перпендикуляр длиной 8 см и наклонная, проекция которой на прямую равна 6 см. Длина наклонной равна …
А. 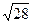 см. Б. 9 см. В. 10 см. Г. величине, отличной от приведенных.
см. Б. 9 см. В. 10 см. Г. величине, отличной от приведенных.
19. В прямоугольном треугольнике АВС угол А равен 40°. Сравните катеты АС и ВС.
А. A С < B C. Б. A C = B C. В. A C > B C. Г. Сравнить нельзя.
20. Углы равнобедренной трапеции могут быть равны ...
А. 35° и 155°. Б. 50° и 40°. В. 120° и 150°. Г. 75° и 105°.
21. В прямоугольном треугольнике один из углов равен 60°, а гипотенуза — 20 см. Чему равен меньший катет?
А. 10 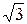 см . Б. 8
см . Б. 8 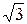 см. В. 10 см. Г. 8 см.
см. В. 10 см. Г. 8 см.
22. Сколько диагоналей можно провести из одной вершины пятиугольника?
А. 3. Б. 2. В. 4. Г. 1.
23. Из точки, лежащей вне круга, проведены к окружности, ограничивающей этот круг, две взаимно перпендикулярные касательные, длиной 8 см каждая. Радиус круга равен …
А. 4 см. Б. 8 см. В. 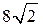 см. Г. величине, отличной от приведенных.
см. Г. величине, отличной от приведенных.
24. Как изменится площадь равнобедренного треугольника, если ее основание уменьшить в 3 раза, а высоту увеличить вдвое?
А. Уменьшится в 6 раз. Б. Увеличится в 2 раза.
В. Увеличится в 3 раза. Г. Уменьшится в 1,5 раза.
25. В круге диаметром 26 см проведена хорда, удаленная от центра на 5 см. Длина хорды равна ...
А. 12 см. Б. 18 см. В. 24 см. Г. величине, отличной от приведенных.
Базовый уровень. Вариант 3.
1. Вычислите: 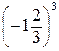 .
.
А. 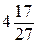 . Б.
. Б. 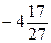 . В. -
. В. - 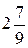 . Г.
. Г. 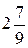 .
.
2. Вычислите значение выражения 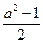 при
при 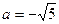 .
.
А. –1. Б. 2. В. 1. Г. –2.
3. Вычислите значение выражения 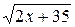 при х = –5.
при х = –5.
А. ±5. Б. 25. В. 5. Г. ±25.
4. Между какими двумя последовательными натуральными числами находится число 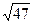 ?
?
А. 6 и 7. Б. 5 и 6. В. 7 и 8. Г. 4 и 5.
5. Сравните числа a = –3,472 и b = –3,742.
А . a = b. Б . a < b. В . a > b. Г . Сравнить нельзя.
6. Упростите выражение 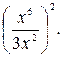
А. 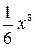 . Б.
. Б. 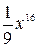 . В.
. В. 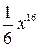 . Г.
. Г. 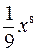 .
.
7. Упростите выражение 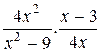 .
.
А. 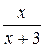 . Б.
. Б. 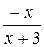 . В.
. В. 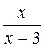 . Г.
. Г. 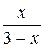 .
.
8. Укажите все значения x, при которых имеет смысл выражение 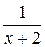 .
.
А. х > –2. Б. x < –2. В. x ¹ 2. Г. x ¹ –2.
9. Из формулы s = 2 + v × t выразите переменную t .
А. t = 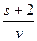 . Б. t = vЧ(s – 2). В.
. Б. t = vЧ(s – 2). В. 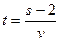 . Г.
. Г. 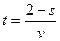 .
.
10. Корнями уравнения (x – 2)(х + 3) = 0 являются числа …
А. 2 и 3. Б. –2 и 3. В. –2 и –3. Г. 2 и –3.
11. Сравните числа а и b, если b – a = 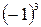 .
.
А . а < b. Б . a > b. В . a = b. Г . a 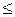 b.
b.
12. График функции у = 3х – 2 проходит через точку…
 А.(–1; –5). Б.(–1; 5). В.
А.(–1; –5). Б.(–1; 5). В. 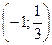 . Г.(–1;1)
. Г.(–1;1)
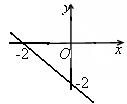
13. На рисунке изображен график функции …
А . y = x + 2. Б . y = –x + 2. В . y = –x – 2. Г . y = x – 2.
14. На рисунке представлен график движения пешехода из пункта А в пункт В, где s – расстояние от пешехода до пункта В, t — время движения. Сколько километров пройдено пешеходом до привала?
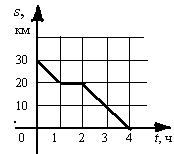 А. 20 км. Б. 10 км. В. 1 км. Г. 2 км.
А. 20 км. Б. 10 км. В. 1 км. Г. 2 км.
15. В классе 20% учащихся изучают только английский язык, 32% — только французский, а остальные 12 человек — только немецкий. Сколько учеников в классе?
А. 24. Б. 20. В. 32. Г. 25.
16. Какая из точек А(2;–5), В(3;2), С(–4;1), D(–1;–2) расположена ближе всех к оси х?
А. A. Б. B. В. C. Г. D.
17. Через точку А(2; –3) проведена прямая, параллельная оси у. Точка ее пересечения с осью х имеет координаты…
А. (0; 2). Б. (2; 0). В. (0; –3). Г. (–3; 0).
18. Из одной точки, лежащей вне прямой, проведены к этой прямой перпендикуляр и наклонная длиной 13 см, проекция которой равна 9 см. Найдите длину перпендикуляра.
А. 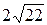 см. Б.
см. Б. 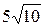 см. В. 44 см. Г. 125 см.
см. В. 44 см. Г. 125 см.
19. В прямоугольном треугольнике АВС угол А равен 69°. Сравните катеты АС и ВС.
A. AC < BC. Б . AC = BC. B. AC > BC. Г. Сравнить нельзя.
20. Углы параллелограмма не могут быть равными ...
А. 35° и 145°. Б. 50° и 130°. В. 20° и 70°. Г. 75° и 105°.
21. Если в прямоугольнике угол между диагональю и меньшей стороной равен 60º, а меньшая сторона равна 12 см, то диагональ прямоугольника равна ...
А. 18 см. Б. 12 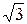 см. В. 24
см. В. 24 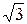 см. Г. 24 см.
см. Г. 24 см.
22. Сколько диагоналей можно провести из одной вершины семиугольника?
А. 5. Б. 4. В. 3. Г. Ответ отличен от приведенных.
23. Из точки, лежащей вне круга, проведены к окружности, ограничивающей этот круг, две взаимно перпендикулярные касательные, длиной 9 см каждая. Диаметр круга равен …
А. 4,5 см. Б. 9 см. В. 18 см. Г. величине, отличной от приведенных.
24. Как изменится площадь прямоугольного треугольника, если один катет увеличить в 2 раза, а другой уменьшить в 4 раза?
А. Увеличится в 2 раза. Б. Уменьшится в 2 раза.
В. Уменьшится в 3 раза. Г. Не изменится.
25. В круге диаметром 20 см проведена хорда длиной 12 см. Ее расстояние от центра равно ...
А. 8 см Б. 16 см. В. 4 см. Г. величине, отличной от приведенных.
Подсказки к заданиям базового уровня
1. Преобразуйте смешанное число в неправильную дробь. Воспользуйтесь правилом возведения дроби в степень:
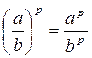 .
.
2. Воспользуйтесь определением квадратного корня, определением арифметического квадратного корня и следствием из него.
Дата: 2018-11-18, просмотров: 893.