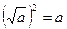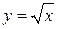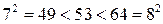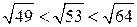4. Возведите предложенные в ответах числа и заданный арифметический квадратный корень в квадрат и сравните полученные числа. Примените равенство . Воспользуйтесь тем, что большему значению аргумента х функции  соответствует большее значение функции. Например, так как , то  или 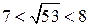, то есть число  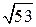заключено между двумя последовательными натуральными числами 7 и 8.

5. Вначале сравните модули чисел а и b. Затем воспользуйтесь следующим свойством числовых неравенств.

  Если а < b и с — отрицательное число, то ac > bc

  Если обе части верного неравенства умножить или разделить на одно и то же отрицательное число и изменить знак неравенства на противоположный, то получится верное неравенство.

Используйте тот факт, что если a > b, то –a < –b. 

6. Вначале выполните действия в скобках, применив правило деления степеней с равными основаниями, а затем возведите полученное выражение в заданную степень, используя правило возведения произведения в степень и правило возведения степени в степень.

Для любого числа а и произвольных натуральных чисел m и n £ m имеет место равенство .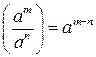

При делении степеней с одинаковыми основаниями основание оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя.

Для любого числа а и произвольных натуральных чисел m и n имеет место равенство ( a^m ) ⁿ = a^mn .

При возведении степени в степень основание оставляют тем же, а показатели степеней перемножают.

Для любых чисел а и b и произвольного натурального числа n имеет место равенство ( ab ) ⁿ = aⁿbⁿ .

При возведении в степень произведения достаточно возвести в эту степень каждый множитель и результаты перемножить.

Не ошибитесь при возведении числа в натуральную степень:  .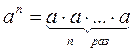

7. Разложите знаменатель на множители, воспользовавшись формулой разности квадратов двух выражений, и сократите полученную дробь, применив основное свойство дроби.

Разность квадратов двух выражений равна произведению разности этих выражений и их суммы: a ² – b ² = ( a – b )( a + b )

Для любых значений а, b и с, где b ¹ 0 и с ¹ 0, верно равенство

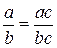 или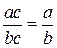

8. Воспользуйтесь тем, что дробь имеет смысл, если ее знаменатель отличен от нуля.

Чтобы найти, при каких значениях х рациональная дробь 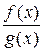 имеет смысл, нужно найти, при каких значениях х знаменатель дроби обращается в нуль, то есть решить уравнение g ( x ) = 0, а затем исключить корни этого уравнения из множества действительных чисел.

9. Воспользуйтесь правилами решения линейного уравнения.

Если к обеим частям уравнения прибавить или от обеих частей уравнения отнять одно и то же число, то получим уравнение, имеющее те же корни, что и данное.