Вначале перенесите члены, не содержащие переменной, выражение для которой нужно получить, в одну сторону, а члены с этой переменной — в другую. Получите уравнение вида ax = b, где а ¹ 0. Отсюда найдите выражение для указанной переменной.
10. Используйте тот факт, что произведение ху равно нулю тогда и только тогда, когда хотя бы один из множителей х или у равен нулю. Осталось приравнять каждый множитель нулю.
11. Воспользуйтесь определением неравенства.
Число а больше числа b , если разность а – b — положительное число; число а меньше числа b , если разность а – b — отрицательное число.
Установите знак правой части равенства.
12. Обратите внимание на то, что во всех приведенных ответах абсцисса искомой точки одна и та же. Формула, которой задана данная функция, позволяет для любого значения аргумента найти соответствующее значение функции путём вычислений.
13. Воспользуйтесь тем, что прямая является графиком линейной функции у = k х + b , где угловой коэффициент к характеризует угол наклона прямой к оси х , а параметр b равен ординате точки пересечения прямой с осью у.
14. График движения представляет собой ломаную, первый отрезок которой характеризует движение до привала. Следующий горизонтальный отрезок характеризует привал, последнее звено ломаной — движение после привала. На оси абсцисс представлено время движения, на оси ординат — пройденное расстояние. По условию установите, какой участок графика необходимо рассмотреть для получения ответа и какую координату — абсциссу или ординату — нужно для этого использовать.
15. Воспользуйтесь правилом нахождения числа по его проценту.
Если число b составляет р процентов от искомого числа а, то, чтобы найти число а, нужно число b разделить на р и умножить на 100: 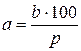 . .
| Капустой заняли 15 га, что составляет 5% площади поля. Площадь поля равна 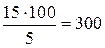 га. га.
|
Определите вначале, сколько процентов от численности учащихся в классе составляет известное количество учащихся, приняв количество учащихся в классе за 100 %, а потом найдите число по его проценту.
16. Воспользуйтесь следующими утверждениями.
Расстояние от точки А(х; у) до оси х равно | у | .
Расстояние от точки А(х; у) до оси у равно | х | .
Установите по условию, расстояния точек до какой оси нужно сравнить, выберите из приведенных то утверждение, которое нужно использовать и сравните модули соответствующих координат всех приведенных точек.
17. Воспользуйтесь следующими утверждениями.
Уравнение прямой, параллельной оси х, имеет вид: у = b , где b ¹ 0.
Прямая у = b пересекает ось у в точке с координатами (0; b ).
Уравнение прямой, параллельной оси у, имеет вид: х = а, где а ¹ 0.
Прямая х = а пересекает ось х в точке с координатами (а; 0).
Сравните абсциссу (ординату) точки пересечения с абсциссой (ординатой) точки А.
18. Примените теорему Пифагора.
В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
19. Воспользуйтесь соотношениями между сторонами и углами в треугольнике и свойствами углов прямоугольного треугольника.
В треугольнике против большей стороны лежит больший угол.
В треугольнике против большего угла лежит большая сторона.
Сумма острых углов прямоугольного треугольника равна 90 ° .
20. Примените определение параллелограмма (трапеции) и свойство параллельных прямых.
Параллелограммом называют четырёхугольник, противоположные стороны которого попарно параллельны.
Трапецией называют четырёхугольник, у которого две стороны параллельны, а две другие не параллельны.
Если две параллельные прямые пересекает третья, то сумма внутренних односторонних углов равна 180 ° .
21. Воспользуйтесь соотношениями между сторонами и углами в треугольнике, свойствами прямоугольного треугольника.
В треугольнике против большей стороны лежит больший угол.
В треугольнике против большего угла лежит большая сторона.
Сумма острых углов прямоугольного треугольника равна 90 ° .
В прямоугольном треугольнике с углом 30 ° катет, лежащий против этого угла, равен половине гипотенузы.
22. Каждую вершину п-угольника можно соединить отрезком со всеми остальными (п – 1) вершинами. Два из этих отрезков — это стороны п-угольника, остальные — диагонали.
23. Воспользуйтесь следующими утверждениями.
Отрезки касательных, проведенных к окружности из одной точки, ограниченные этой точкой и точками касания, равны между собой.
Радиус, проведенный в точку касания, перпендикулярен касательной.
24. Воспользуйтесь формулой площади указанного многоугольника.
Площадь прямоугольника равна произведению его смежных сторон.
Площадь прямоугольного треугольника равна половине произведения его катетов.
Площадь треугольника равна половине произведения её стороны и высоты, проведенной на эту сторону.
Введите обозначения для указанных элементов многоугольника, выразите через них исходную его площадь, изменённые элементы и изменённую площадь.
25. Воспользуйтесь теоремой Пифагора.
В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
Соедините центр круга с концами и с серединой хорды.
Основной уровень Вариант 1
1. Вычислите: 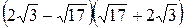 .
.
А. –11. Б. 11. В. 5. Г. –5
2. Вычислите значение выражения 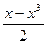 при x = –
при x = – 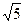 .
.
А. 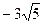 . Б.
. Б. 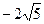 . В.
. В. 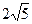 . Г.
. Г. 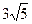 .
.
3. Найдите значение выражения 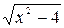 при
при 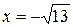 .
.
А. 3. Б. –3. В. ± 3. Г. Не имеет смысла.
4. Расположите в порядке возрастания числа 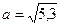 ,
, 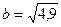 ,
, 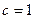 .
.
А . c < a < b. Б . c < b < a. В . b < c < a. Г. b < a < c.
5. Сравните числа 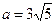 и
и 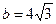 .
.
А. a < b. Б. a = b. В. a > b. Г. Сравнить нельзя.
6. Упростите выражение 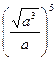 .
.
А. 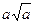 . Б.
. Б. 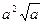 . В.
. В. 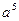 . Г.
. Г. 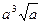 .
.
7. Упростите выражение 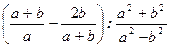 .
.
А. 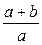 . Б.
. Б. 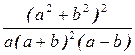 . В.
. В. 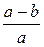 . Г.
. Г. 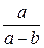 .
.
8. Укажите все значения x, при которых имеет смысл выражение 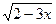 .
.
А. 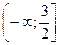 . Б.
. Б. 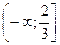 . В.
. В. 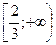 . Г.
. Г. 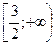 .
.
9. В цепи электрического тока два сопротивления R1 и R2 соединены параллельно. Общее сопротивление R связано с R1 и R2 формулой 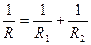 . Выразите R через R1 и R2.
. Выразите R через R1 и R2.
А. 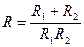 . Б.
. Б. 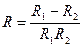 . В.
. В. 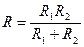 . Г.
. Г. 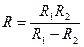 .
.
10. Один из корней уравнения 18x2 + 23x + 5 = 0 равен –1. Второй его корень равен … А. 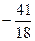 . Б.
. Б. 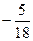 . В.
. В. 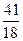 . Г.
. Г. 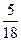 .
.
11. Сравните числа а и b, если разность b – a представляет собой квадрат некоторого числа.
А. a = b. Б. a £ b. В. a > b. Г. Сравнить нельзя.
12. Задайте формулой обратную пропорциональность, зная, что ее график проходит через точку с координатами (–3; 4).
А. 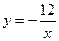 . Б.
. Б. 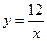 . В.
. В. 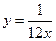 . Г.
. Г. 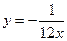 .
.
13. Какой из приведенных графиков может быть графиком функции 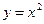 ?
?

14. 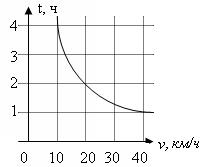
 На рисунке дан график зависимости времени t, затрачиваемого на путь из пункта А в пункт В, от скорости v движения, представляющей собой обратную пропорциональность. Какое время понадобится на путь из А в В, если двигаться со скоростью, меньшей 10 км/ч?
На рисунке дан график зависимости времени t, затрачиваемого на путь из пункта А в пункт В, от скорости v движения, представляющей собой обратную пропорциональность. Какое время понадобится на путь из А в В, если двигаться со скоростью, меньшей 10 км/ч?
А. 4 часа. Б. Меньше 4 ч. В. Больше 4 ч.
Г. Определить нельзя.
15. Смешали 2 литра 25% раствора кислоты и 4 литра 10% раствора той же кислоты. Концентрация полученного раствора равна …
А. 35%. Б. 15%. В. 17,5%. Г. 20%.
16. Какая из приведенных точек находится на том же расстоянии от оси x, что и точка с координатами (–3;4)?
 А. (–3; 2). Б. (3; 1). В. (–4; –3). Г. (–1; 4).
А. (–3; 2). Б. (3; 1). В. (–4; –3). Г. (–1; 4).
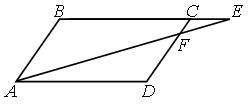
17. На рисунке ABCD — параллелограмм, AD = 12 см, CE = 4 см. Отношение площадей треугольников ABE и CFE равно...
А. 4:1. Б. 8:1. В. 64:1. Г. 16:1.
18. В прямоугольной трапеции основания равны 5 см и 17 см, а большая боковая сторона 13 см. Высота трапеции равна …
А. 12 см. Б. 11 см. В. 5 см. Г. 8 см.
19. В равнобедренном треугольнике угол при основании равен 70°. Сравните высоту h и половину основания 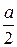 .
.
А. Сравнить нельзя. Б. 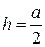 . В.
. В. 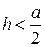 . Г.
. Г. 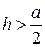 .
.
20. Два неравных отрезка в точке пересечения делятся пополам, их концы последовательно соединены. Полученный четырехугольник является …
А. параллелограммом. Б. ромбом. В. прямоугольником. Г. квадратом.
21. Сторона ромба равна 6 см, острый угол 60°. Диагонали ромба равны …
А. 6 и 12 см. Б. 6 и 6 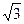 см. В. 3 и 3
см. В. 3 и 3 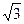 см. Г. 3 и 6
см. Г. 3 и 6 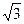 см.
см.
22. Две параллельные прямые пересечены тремя параллельными прямыми. Сколько образовалось параллелограммов?
А. 6. Б. 4. В. 2. Г. 3.
23. Четырехугольник ABCD — прямоугольная трапеция (АВ ^ AD, ÐAD С — тупой), АС — ее диагональ, MN — средняя линия, M Î AB, N Î CD, K — точка пересечения АС и MN. Сравните отрезки MK и NK.
А . MK > NK. Б . MK = NK. В. MK < NK. Г. Сравнить нельзя.
24. 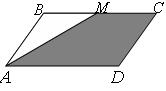 Площадь параллелограмма ABCD равна S, MB = MC. Чему равна площадь закрашенной фигуры?
Площадь параллелограмма ABCD равна S, MB = MC. Чему равна площадь закрашенной фигуры?
А. 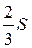 . Б.
. Б. 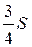 . В.
. В. 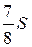 . Г.
. Г. 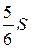 .
.
25. В прямоугольной трапеции основания равны 10 и 6 см, а большая боковая сторона равна 5 см. Площадь трапеции равна ...
А. 48 см2. Б. 24 см2. В. 12 см2. Г. 36 см2.
Основной уровень Вариант 2
1. Вычислите: 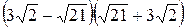 .
.
А. 3. Б. 15. В. –3. Г. –15.
2. Вычислите значение выражения 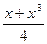 при
при 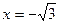 .
.
А. 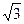 . Б.
. Б. 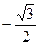 . В.
. В. 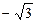 . Г.
. Г. 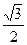 .
.
3. Найдите значение выражения 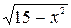 при
при 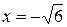 .
.
А. 3. Б. –3. В. ± 3. Г. Не имеет смысла.
4. Расположите в порядке возрастания числа 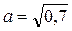 ,
, 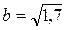 ,
, 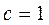 .
.
А . а < b < c. Б . c < a < b. В . c < b < a. Г . a < c < b.
5. Сравните числа 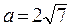 и
и 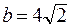 .
.
А. Сравнить нельзя. Б. a = b . В. a > b. Г. a < b.
6. Упростите выражение 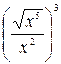 .
.
А. 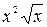 . Б.
. Б. 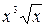 . В.
. В. 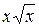 . Г.
. Г. 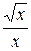 .
.
7. Упростите выражение 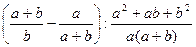 .
.
А. 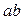 . Б.
. Б. 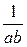 . В.
. В. 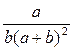 . Г.
. Г. 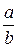 .
.
8. Укажите все значения x, при которых имеет смысл выражение 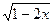 .
.
А. 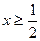 . Б.
. Б. 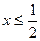 . В.
. В. 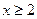 . Г.
. Г. 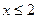 .
.
9. В цепи электрического тока два сопротивления R1 и R2 соединены параллельно. Общее сопротивление R связано с R1 и R2 формулой 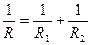 . Выразите R1 через R и R2.
. Выразите R1 через R и R2.
А. 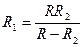 . Б.
. Б. 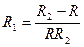 . В.
. В. 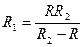 . Г.
. Г. 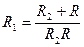 .
.
10. Один из корней уравнения 28x2 + 23x – 5 = 0 равен –1. Второй его корень равен …
А. 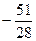 . Б.
. Б. 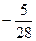 . В.
. В. 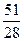 . Г.
. Г. 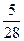 .
.
11. Сравните числа а и b, если разность a – b является квадратом некоторого числа.
А. a < b. Б. a = b. В. a ³ b. Г. Сравнить нельзя.
12. Задайте формулой обратную пропорциональность, зная, что ее график проходит через точку с координатами (–25; –0,2).
А. 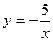 . Б.
. Б. 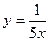 . В.
. В. 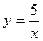 . Г.
. Г. 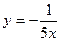 .
.
13. Какой из приведенных графиков может быть графиком функции 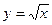 ?
?

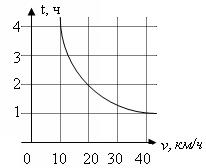
14.  На рисунке дан график зависимости времени t, затрачиваемого на путь из пункта А в пункт В, от скорости v движения, представляющей собой обратную пропорциональность. С какой скоростью v надо двигаться, чтобы добраться из А в В менее, чем за 2 часа ?
На рисунке дан график зависимости времени t, затрачиваемого на путь из пункта А в пункт В, от скорости v движения, представляющей собой обратную пропорциональность. С какой скоростью v надо двигаться, чтобы добраться из А в В менее, чем за 2 часа ?
А. v = 20 км/ч. Б. v < 20 км/ч. В. v > 20 км/ч.
Г. Определить нельзя.
15. Смешали 5 литров 20% раствора кислоты и 3 литра 40% раствора той же кислоты. Концентрация полученного раствора равна …
А. 30%. Б. 25%. В. 35%. Г. 27,5%.
16.  Какая из приведенных точек находится на том же расстоянии от оси y, что и точка с координатами (–2; 3)?
Какая из приведенных точек находится на том же расстоянии от оси y, что и точка с координатами (–2; 3)?
А. (1; 3). Б. (1; –3). В. (–2; –2). Г. (–3; 2).
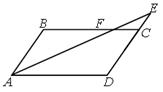
17. На рисунке ABCD — параллелограмм, AB = 8 см, CE = 2 см. Отношение площадей треугольников ADE и FCE равно ...
А. 20:1. Б. 40:1. В. 25:1. Г. 45:2.
18. В равнобедренном треугольнике основание и боковая сторона равны соответственно 12 см и 10 см. Высота, опущенная на его основание, равна …
А. 6 см. Б. 13 см. В. 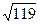 см. Г. 8 см.
см. Г. 8 см.
19. Из вершины В тупого угла равнобедренной трапеции АВС D проведён перпендикуляр В F на основание AD. ÐВ AD = 41°. Сравните длины отрезков А F и BF.
А. Сравнить нельзя. Б. BF = AF. В . BF > AF. Г . BF < AF.
20. Два равных отрезка в точке пересечения делятся пополам, их концы последовательно соединены отрезками. Полученный четырехугольник является …
А. трапецией. Б. квадратом. В. ромбом. Г. прямоугольником.
21. Меньшая сторона прямоугольника равна 3 дм, а угол между диагоналями равен 120°. Большая сторона прямоугольника и его диагональ соответственно равны …
А. 6 дм, 3 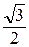 дм. Б. 3
дм. Б. 3 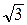 дм, 6 дм. В. 3
дм, 6 дм. В. 3 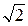 дм, 3 дм. Г. 5 дм, 3
дм, 3 дм. Г. 5 дм, 3 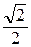 дм.
дм.
22. Три параллельные прямые пересечены тремя параллельными прямыми. Сколько получилось параллелограммов?
А. 4. Б. 6. В. 8. Г. 9.
23. 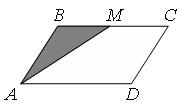 Четырёхугольник ABCD — трапеция (ВС ½½ AD), ВС < AD, АС — ее диагональ, MN — средняя линия, M Î AB, N Î CD, K — точка пересечения AC и MN. Сравните отрезки M K и N K.
Четырёхугольник ABCD — трапеция (ВС ½½ AD), ВС < AD, АС — ее диагональ, MN — средняя линия, M Î AB, N Î CD, K — точка пересечения AC и MN. Сравните отрезки M K и N K.
А. MK = NK. Б. MK < NK. В. MK > NK. Г. Сравнить нельзя.
24. Площадь параллелограмма ABCD равна S, M — середина стороны BC. Чему равна площадь закрашенной фигуры?
А. 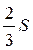 . Б.
. Б. 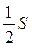 . В.
. В. 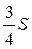 . Г.
. Г. 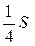 .
.
25. В прямоугольной трапеции основания равны 20 и 12 см, а меньшая диагональ равна 13 см. Площадь трапеции равна ...
А. 160 см2. Б. 40 см2. В. 96 см2. Г. 80 см2.
Основной уровень. Вариант 3.
1. Вычислите: 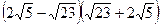 .
.
А. –3. Б. 13. В. 3. Г. –13.
2. Вычислите значение выражения 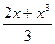 при x =
при x = 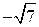 .
.  .
.
А. 3 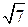 . Б.
. Б. 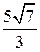 . В. –3
. В. –3 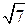 . Г. –
. Г. – 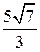 .
.
3. Найдите значение выражения 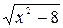 при
при 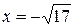 .
.
А. –3. Б. 3. В. ± 3. Г. Не имеет смысла.
4. Расположите числа 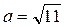 ,
, 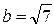 , с = 3 в порядке убывания.
, с = 3 в порядке убывания.
А . a > b > c. Б . с > a > b. В . с > b > a. Г. a > c > b.
5. Сравните числа 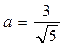 и
и 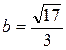 .
.
А. a = b. Б. a < b. В. a > b. Г. Сравнить нельзя.
6. Упростите выражение 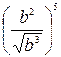 .
.
А. 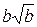 . Б.
. Б. 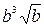 . В.
. В. 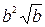 . Г.
. Г. 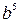 .
.
7. Упростите выражение 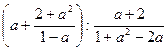 .
.
А. a – 1. Б. a + 1. В. 1 – a. Г. 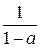 .
.
8. Укажите все значения x, при которых выражение 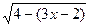 не имеет смысла.
не имеет смысла.
А. 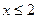 . Б.
. Б. 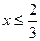 . В.
. В. 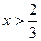 . Г.
. Г. 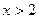 .
.
9. Из формулы 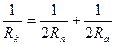 дающей соотношение между радиусом кривизны Rk орбиты и расстояниями перигея R п и апогея R а от центра Земли, выразите Rn через остальные переменные.
дающей соотношение между радиусом кривизны Rk орбиты и расстояниями перигея R п и апогея R а от центра Земли, выразите Rn через остальные переменные.
А. 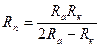 . Б.
. Б. 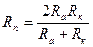 . В.
. В. 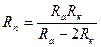 . Г.
. Г. 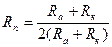 .
.
10. Один из корней уравнения 3x2 – 7x + 2 = 0 равен 2. Второй его корень равен …
А. 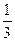 . Б.
. Б. 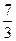 . В.
. В. 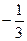 . Г.
. Г. 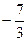 .
.
11. Сравните числа а и b, если разность b – a представляет собой куб положительного числа.
А. a = b. Б. a > b. В. a < b. Г. Сравнить нельзя.
12. 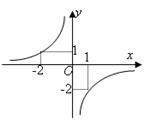 На рисунке изображен график функции y =
На рисунке изображен график функции y = 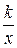 . Коэффициент k равен ...
. Коэффициент k равен ...
A . – 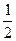 . Б. 2. В.
. Б. 2. В. 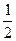 . Г. –2.
. Г. –2.
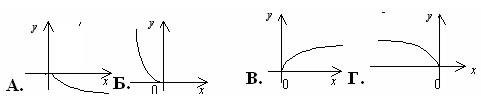
13. На каком рисунке изображен график функции y = 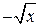 ?
?
14. 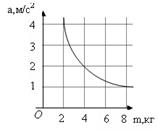
 На рисунке дан график зависимости ускорения а движущегося тела от его массы m при постоянной силе F, действующей на это тело (F = ma). Каким ускорением обладает тело, масса которого меньше 4 кг?
На рисунке дан график зависимости ускорения а движущегося тела от его массы m при постоянной силе F, действующей на это тело (F = ma). Каким ускорением обладает тело, масса которого меньше 4 кг?
А. a = 2 м/с2. Б. a < 2 м/с2. В. a > 2 м/с2. Г. Определить нельзя.
15. Два литра некоторого фруктового сока имеют концентрацию сахара 10%, а три литра другого — 15%. Какова концентрация сахара в их смеси?
А. 25 %. Б. 13 %. В. 12,5 %. Г. 5 %.
16.  Какая из приведенных точек находится на том же расстоянии от начала координат, что и точка (8; –6)?
Какая из приведенных точек находится на том же расстоянии от начала координат, что и точка (8; –6)?
А. (4; 3). Б. (–6;10). В. (–8; –6). Г. (10; 6).
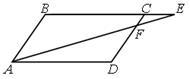
17. На рисунке ABCD – параллелограмм. AD = 12 см, CE = 4 см, CF = 2 см. Длина стороны AB равна ...
А. 6 см. Б. 9 см. В. 10 см. Г. 8 см.
18. Основания прямоугольной трапеции равны 10 см и 15 см, большая боковая сторона равна 13 см. Меньшая боковая сторона трапеции равна …
А.6 см Б.7,5 см. В.10 см. Г.12 см.
19. Из вершины С тупого угла прямоугольной трапеции АВС D проведён перпендикуляр С F на основание AD. ÐADC = 47°. Сравните длины отрезков А B и DF.
А. Сравнить нельзя. Б. DF = AB. В . DF > AB. Г . DF < AB.
20. Какую фигуру образуют прямые, последовательно соединяющие середины сторон прямоугольника?
А. Прямоугольник. Б. Квадрат. В. Ромб. Г. Трапецию.
21. В равнобедренной трапеции острый угол равен 60°, боковая сторона равна 8 см, а большее основание 14 см. Средняя линия и высота трапеции соответственно равны …
А. 6 см и 2 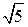 см. Б. 11 см и 4
см. Б. 11 см и 4 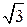 см. В. 10 см и 4
см. В. 10 см и 4 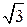 см. Г. 9 см и 2
см. Г. 9 см и 2 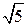 см.
см.
22. Два луча, выходящие из одной точки, пересечены тремя параллельными прямыми. Сколько при этом получилось трапеций?
А. 2. Б. 3. В. 4. Г. 6.
23. Четырехугольник ABCD — прямоугольная трапеция (АВ ^ AD, ÐAD С — тупой), BD — ее диагональ, MN — средняя линия, M Î AB, N Î CD, K — точка пересечения BD и MN. Сравните отрезки MK и NK.
А. Сравнить нельзя. Б. MK = NK. В. MK > NK. Г. MK < NK.
24. 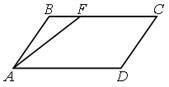 В параллелограмме ABCD BF:FC = 1:3. Площади треугольника ABF и четырехугольника AFCD относятся как ...
В параллелограмме ABCD BF:FC = 1:3. Площади треугольника ABF и четырехугольника AFCD относятся как ...
А. 1:3. Б. 1:9. В. 1:5. Г. 1:7.
25. В равнобедренной трапеции основания равны 4 см и 20 см, а боковая сторона равна 10 см. Площадь трапеции равна ...
А. 144 см2. Б. 36 см2. В. 72 см2. Г. 96 см2.
Подсказки к заданиям основного уровня
1. Воспользуйтесь формулой произведения разности двух выражений и их суммы, правилом возведения произведения в степень и следствием из определения арифметического квадратного корня.
Произведение разности двух выражений и их суммы равно разности квадратов этих выражений: ( a – b )( a + b ) = a 2 – b 2 .
Для любых чисел а и b и произвольного натурального числа n имеет место равенство ( ab ) n = anbn .
При любом а, при котором выражение 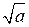 имеет смысл, справедливо равенство
имеет смысл, справедливо равенство 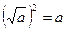 .
.
2. Вначале преобразуйте данное выражение, выполнив вынесение общего множителя в числителе за скобки, затем подставьте заданное значение переменной. Воспользуйтесь следствием из определения арифметического квадратного корня.
Для разложения многочлена на множители способом вынесения общего множителя за скобки нужно:
1) в членах многочлена выделить общий множитель;
Дата: 2018-11-18, просмотров: 3423.