В течение полугода увеличить долю рынка на 5% за счет снижения цены аппарата и создания разветвленной сети продажи предоплаченных телефонных карт.

Корпорация «Ford» (финансовая цель)

Достичь в течение года роста рентабельности собственного капитала — на 20—25%, привлеченного капитала — не ниже 27%.

В зависимости от времени достижения цели организации можно разделить на две категории:

1) краткосрочные цели организации направлены на достижение текущих улучшений и результатов, их успешная реализация способствует достижению долгосрочных целей;

2) долгосрочные цели организации — на укрепление положения фирмы и улучшение показателей ее работы в долгосрочной перспективе.

Цели формулируются как для организации в целом (общие цели), так и для отдельных ее подразделений. При этом очень важно, чтобы они были тщательно согласованы между собой.

Цели должны быть сформулированы таким образом, чтобы их достижение требовало напряжения сил всех работников организации. При этом возможно, чтобы на начальном этапе цели обеспечивали хотя бы незначительное увеличение производительности. Впоследствии они должны устанавливаться на уровне, позволяющем значительно улучшить положение организации относительно ее ближайших конкурентов и требующем максимально полной мобилизации внутреннего потенциала.

Алгоритм поиска компромиссов

Примером алгоритма поиска компромиссов является сортировка подсчётом

Сортировка подсчётом — алгоритм сортировки, в котором используется диапазон чисел сортируемого массива (списка) для подсчёта совпадающих элементов. Применение сортировки подсчётом целесообразно лишь тогда, когда сортируемые числа имеют (или их можно отобразить в) диапазон возможных значений, который достаточно мал по сравнению с сортируемым множеством, например, миллион натуральных чисел меньших 1000. Эффективность алгоритма падает, если при попадании нескольких различных элементов в одну ячейку, их надо дополнительно сортировать. Необходимость сортировки внутри ячеек лишает алгоритм смысла, так как каждый элемент придётся просматривать более одного раза.

Предположим, что входной массив состоит из n целых чисел в диапазоне от 0 до k − 1, где 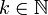. Далее алгоритм будет обобщён для произвольного целочисленного диапазона. Существует несколько модификаций сортировки подсчётом, ниже рассмотрены три линейных и одна квадратичная, которая использует другой подход, но имеет то же название.

Простой алгоритм

Это простейший вариант алгоритма. Создать вспомогательный массив Count[0..k - 1], состоящий из нулей, затем последовательно прочитать элементы входного массива A, для каждого A[i] увеличить Count[A[i]] на единицу. Теперь достаточно пройти по массиву Count[], для каждого 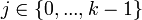в массив A последовательно записать число j Count[j] раз. Введение дополнительного массива Count2, обусловленно тем, что при расстановке значений позиций, ещё не использованные данные затираются новыми.

Proc SimpleCountingSort

 For i=0 to k-1 do

Count[i]=0;

 For i=0 to n-1 do

Count[A[i]]=Count[A[i]]+1;

 For i=0 to k-1 do

Count2[i]:=Count[i];

 Sum=0;

 For i=1 to k-1 do

 Begin

Sum=Sum+Count2[i-1];

Count[i]=Sum;

 End;

 For i=0 to n-1 do

 Begin

c=A[i];

B[Count[c]]=c;

Count[c]=Count[c]+1;

 End;

EndProc

Алгоритм со списком

Этот вариант (англ. pigeonhole sorting, count sort) используется, когда на вход подается массив структур данных, который следует отсортировать по ключам (key). Нужно создать вспомогательный массив C[0..k - 1], каждый C[i] в дальнейшем будет содержать список элементов из входного массива. Затем последовательно прочитать элементы входного массива A, каждый A[i] добавить в список C[A[i].key]. В заключении пройти по массиву C, для каждого 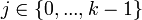в массив A последовательно записывать элементы списка C[j]. Алгоритм устойчив.

ListCountingSort

for i = 0 to k - 1

   C[i] = NULL;

for i = 0 to n - 1

   C[A[i].key].add(A[i]);

b = 0;

for j = 0 to k - 1

   p = C[j];

   while p != NULL

       A[b] = p.data;

       p = p.next();

       b = b + 1;

Устойчивый алгоритм

В этом варианте помимо входного массива A потребуется два вспомогательных массива — C[0..k - 1] для счётчика и B[0..n - 1] для отсортированного массива. Сначала следует заполнить массив C нулями, и для каждого A[i] увеличить C[A[i]] на 1. Далее подсчитывается число элементов меньше или равных текущему. Для этого каждый C[j], начиная с C[1], увеличивают на C[j - 1]. На последнем шаге алгоритма читается входной массив с конца, значение C[A[i]] уменьшается на 1 и в каждый B[C[A[i]]] записывается A[i]. Алгоритм устойчив.

StableCountingSort

for i = 0 to k - 1

   C[i] = 0;

for i = 0 to n - 1

   C[A[i]] = C[A[i]] + 1;

for j = 1 to k - 1

   C[j] = C[j] + C[j - 1];

for i = n - 1 to 0

   C[A[i]] = C[A[i]] - 1;

   B[C[A[i]]] = A[i];