1. Случай неоднородного ДУЧП

Рассмотрим ДУЧП Пуассона:

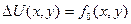
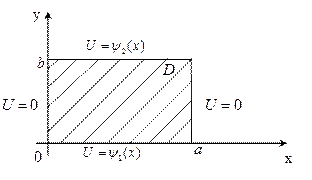
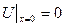
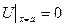
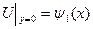
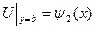
Должно быть согласование граничных условий Дирихле в угловых точках области.

Суть модификации метода Фурье:

Функция  ищется в виде суммы двух функций:

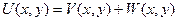, где

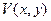 - решение краевой задачи для однородного ДУЧП, соответствующего данному неоднородному ДУЧП.

 - это какое-нибудь решение данного неоднородного ДУЧП. Находится, чаще всего, подбором.

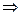Для функци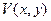й  и  будут следующие краевые задачи:

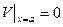
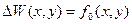
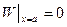
План решения:

1. Функцию 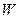 нужно найти подбором
2. Функцию 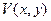 находить методом Фурье

Пример нахождения функций  подбором.

Пусть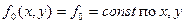

Будем искать (подбирать)  в классе многочленов второй степени относительно :

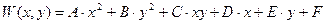
Постоянные  будем находить из сформулированных условий для функции :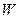

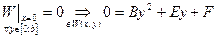 - т.к. равенство должно выполняться , то должно быть .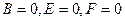

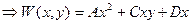
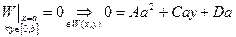 - т.к. это равенство должно выполняться , то должно быть:

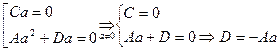
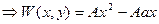
ДУЧП:

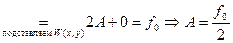
Таким образом, функция  подобралась в следующем виде:

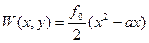
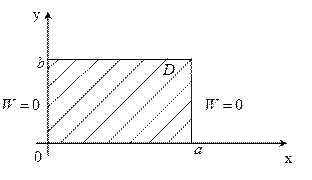
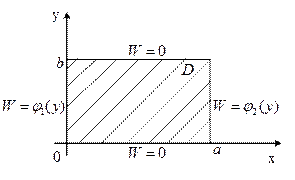
2. Случай: в прямоугольной конечной области отсутствуют нулевые граничные условия на двух противоположных сторонах.

1). Постановка матмодели:

ДУЧП: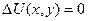

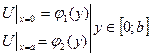
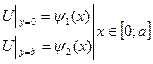
2). Согласование граничных условий:

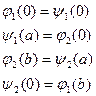
В угловых точках функции должны иметь одно и то же значение (не обязательно нулевое).

3). Суть модификации:

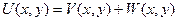, где для функци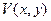й  и  будет получаться краевая задача для того де ДУЧП, но с нулевыми граничными условиями на двух противоположных сторонах прямоугольной области.

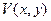
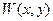
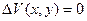
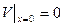
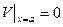
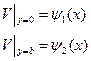
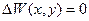
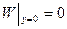
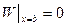
При этом потребуются дополнительные условия согласования: все четыре функции должны быть равны в 0 в угловых точках области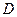

Каждая из функци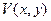й  и 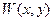 находится методом Фурье, а искомая функция получается их сложением.

3. Для случая полубесконечной прямоугольной области, на двух противоположных сторонах которой нет нулевых граничных условий (хотя бы на одной из них)

1). Постановка матмодели задачи:

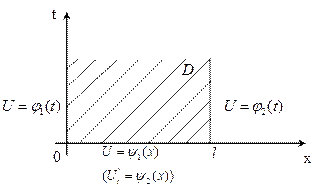
ДУЧП: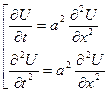

Граничные условия:

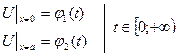
Начальные условия:

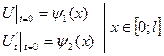 - для волнового уравнения

Хотя бы одна из функци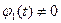й  или

2). Согласование граничных условий:

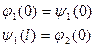
3). Суть модификации:

Искомая функция 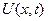 ищется в виде суммы двух функций  и :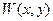

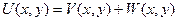, где для одной из этих функций нужно ставить краевую задачу, которую можно решить методом Фурье (с нулевыми граничными условиями), а другую рекомендуется найти методом подбора.

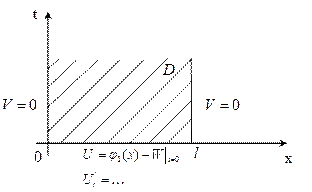ДУЧП: (---------) Граничные условия: Начальные условия (скорректированные):

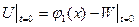
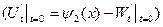
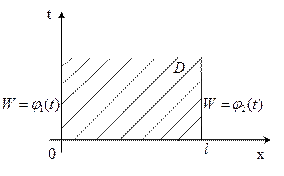ДУЧП: (---------) Граничные условия:

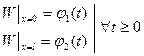
План решения:

1. Функцию 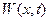, для которой неполная краевая задача, найти подбором.
2. Функцию 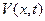, для которой получается скорректированная, но полная краевая задача, найти методом Фурье.