Математическая модель включает в себя:

1. ДУЧП относительно функции 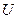 состояния физического процесса (ДУЧП состояния физического процесса)
2. область применения независимых переменных функции состояния .
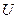3. начальные условия для функции 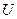 (если они нужны)
4. граничные условия для функции .

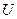Мат. модель в целом называется краевой задачей для ДУЧП

Пример постановки краевой задачи (составления мат. модели физической задачи)

Тонкая струна длины 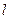 закреплена на концах. В начальный момент времени струна отклонена от равновесия в некоторой своей точке 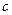, это отклонение равно 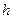. Отклоненная струна отпущена со скоростью  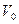одинаковой для всех точек струны.

Требуется найти функцию 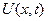, равную отклонению любой точки  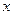на этой струне в любой момент времени .

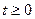Иллюстрация к условию задачи:

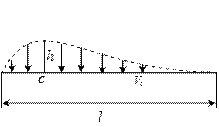
Считаем, что:

1. В оттянутом положении струна имеет вид ломаной, составленной из отрезков, т.е. не учитываем кривизну струны.

2. Т.к. вектор 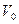 одинаков, то будем иметь поперечные колебания струны в одной плоскости.

3. Колебание струны будет происходить под действием сил упругости, подчиняясь закону Гука

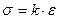
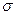 - напряжение на единичную площадку перпендикулярно направлению .

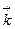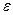 - деформация в направлении .

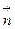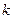 - коэффициент пропорциональности, связанный с модулем Юнга.

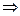из литературы известно, что упругие поперечные колебания струны описываются уравнением:

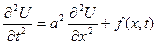, где

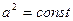 зависит от физических свойств материала струны.

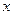 - координата точек струны.

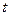 - время.

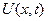 - отклонение точки  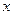от положения равновесия в момент времени .

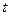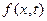 - функция, которая характеризует плотность массовых сил, влияющих на колебания струны (количество сил, приходящихся на единицу массы):

1) Силы сопротивления среды процессу колебания

2) Сила тяжести

3) Сила упругости

4. Если сопротивление среды процессу колебания не учитывать, то колебания струны называются свободными. Они проявятся как незатухающие. Тогда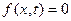

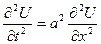 - простейшее волновое уравнение, которое описывает колебания струны.

Его и будем использовать.

Уточнение иллюстрации к условию задачи с учетом выбранного уравнения состояния:

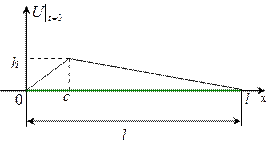
Составим уравнение начального положения струны:

(****************)

 (****************)

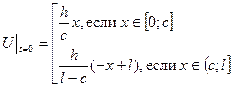
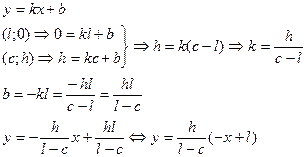
Геометрическая трактовка решения задачи:

Требуется найти функцию 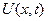, где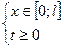

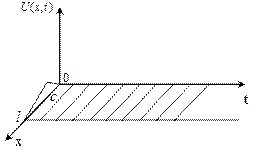
Формулировка математической модели задачи:

1. Требуется найти функцию 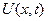 удовлетворяющую дифференциальному уравнению в частных производных;

,

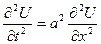где 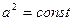 по x и t.

2. независимые переменные x и t изменяются в области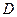

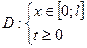
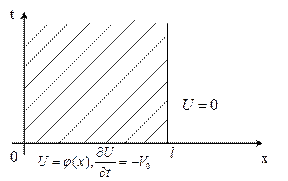
3. начальные условия для функции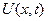

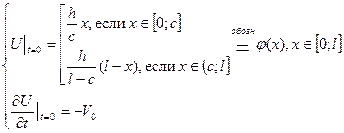
Здесь 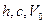 - управляемые параметры задачи, являются константами по x и t.

4. Граничные условия для функци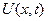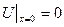и :

 и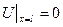

Таким образом, математической моделью поставленной задачи является краевая задача Дирихле для одномерного волнового уравнения (для ДУЧП гиперболического типа).