ДУЧП: 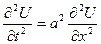
Начальные условия: 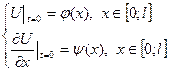
Граничные условия: 
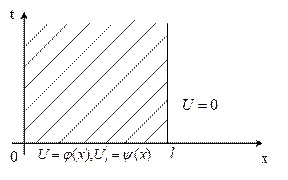
1. Искомую функцию 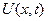 ищем в виде произведения двух функций, каждая из которых зависит только от одной переменной.
ищем в виде произведения двух функций, каждая из которых зависит только от одной переменной.
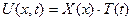 (1)
(1)
Это позволяет разделить переменные в ДУЧП, т.к.
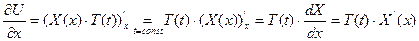
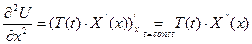
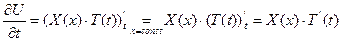
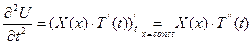
ДУЧП: 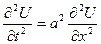
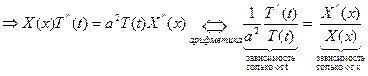
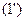
При этих действиях 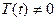 и
и 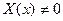 , т.к. в противном случае будет
, т.к. в противном случае будет  , что не удовлетворяет начальным условиям для функции
, что не удовлетворяет начальным условиям для функции 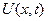 (случай
(случай  равен положению покоя струны).
равен положению покоя струны).
Уравнение с разделенными переменными 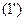 выполняется при любых x и любых t
выполняется при любых x и любых t 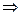 равенство между его левой и правой частями, зависящими только от одного из аргументов x или t, возможно только тогда, когда каждая из частей этого равенства равна
равенство между его левой и правой частями, зависящими только от одного из аргументов x или t, возможно только тогда, когда каждая из частей этого равенства равна 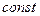 по x и t. Обозначим эту константу
по x и t. Обозначим эту константу 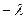 и перейдем от уравнения
и перейдем от уравнения 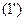 к системе двух уравнений:
к системе двух уравнений:
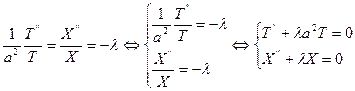 (2)
(2)
Таким образом, в результате разделения переменных ДУЧП заменилось системой двух обыкновенных ДУ, причем оба этих уравнения сохраняют вид ДУЧП: являются ДУ второго порядка по каждой переменной; являются линейными, однородными и с постоянными коэффициентами.
2. Т.к. ДУ в системе (2) получились независимыми друг от друга, то их можно решать последовательно в произвольном порядке. Выберем для начала такое уравнение системы (2), на которое можно перебросить нулевые граничные условия.
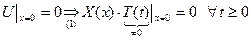
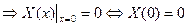
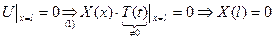
Нулевые граничные условия перебросились на функцию 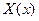 , поэтому сначала будем решать второе ДУ в системе (2).
, поэтому сначала будем решать второе ДУ в системе (2).
3. Будем находить функцию 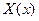 , удовлетворяющую условиям
, удовлетворяющую условиям
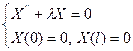 (3)
(3)
Задача Штурма-Лиувилля:
Требуется найти такие числа 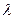 , при которых система (3) имеет нетривиальные решения. Эти числа
, при которых система (3) имеет нетривиальные решения. Эти числа  называются собственными значениями задачи Штурма-Лиувилля. Далее нужно найти функции
называются собственными значениями задачи Штурма-Лиувилля. Далее нужно найти функции 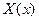 , удовлетворяющие системе (3) при найденных значениях
, удовлетворяющие системе (3) при найденных значениях 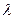 . Эти функции называются собственными функциями задачи Штурма-Лиувилля.
. Эти функции называются собственными функциями задачи Штурма-Лиувилля.
Решение задачи Штурма-Лиувилля.
ДУ: 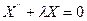 - обыкновенное линейное ДУ второго порядка с постоянными коэффициентами.
- обыкновенное линейное ДУ второго порядка с постоянными коэффициентами.
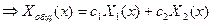 , где
, где
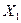 и
и 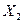 - ФСЧР, т.е. два линейно-независимых частных решения этого ДУ.
- ФСЧР, т.е. два линейно-независимых частных решения этого ДУ.
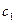 и
и 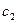 - произвольные константы.
- произвольные константы.
ФСЧР находится с помощью характеристического уравнения:
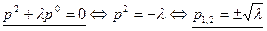
Для записи ФСЧР по корням 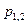 нужно знать, являются ли эти корни:
нужно знать, являются ли эти корни: 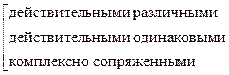 .
.
Это зависит от следующих случаев для 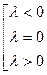
1) если 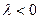 , то
, то 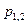 - различные действительные корни.
- различные действительные корни.
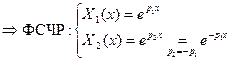
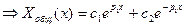
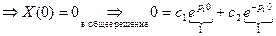
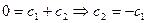
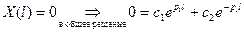
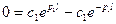
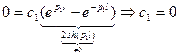
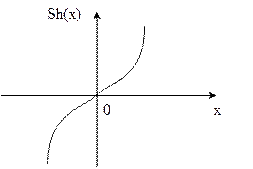
Таким образом, в случае 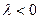 получается только тривиальное решение задачи Штурма-Лиувилля:
получается только тривиальное решение задачи Штурма-Лиувилля:
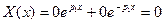
Т.е. при 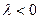 данная задача Штурма-Лиувилля не имеет решения.
данная задача Штурма-Лиувилля не имеет решения.
2) Если 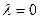 , то
, то 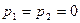 - случай равных действительных корней характеристического уравнения.
- случай равных действительных корней характеристического уравнения.
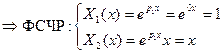
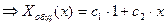
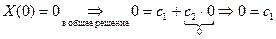
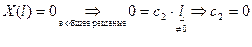
Таким образом, при 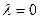 получаем только тривиальное решение задачи 3.
получаем только тривиальное решение задачи 3.
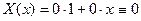
Т.е. при 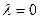 данная задача Штурма-Лиувилля также не имеет решения.
данная задача Штурма-Лиувилля также не имеет решения.
3) Если 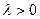 , то
, то
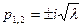 - случай комплексно-сопряженных корней характеристического уравнения, т.е. корней вида:
- случай комплексно-сопряженных корней характеристического уравнения, т.е. корней вида: 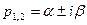
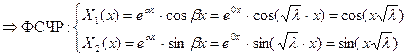
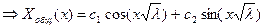
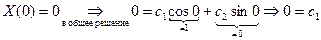
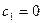
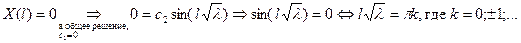
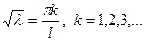
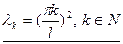 (4)
(4)
Получилось счетное множество собственных чисел задачи Штурма-Лиувилля. Этим собственным числам соответствует так же счетное множество функций задачи Штурма-Лиувилля.
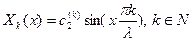
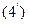
Таким образом, задача Штурма-Лиувилля для системы (3) имеет решение в виде собственных чисел (4) и в виде собственных функций 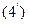 .
.
4. Теперь решаем другое уравнение в системе (2):
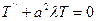 , где
, где
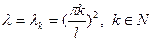
Тип уравнения сохраняется:
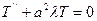 - обыкновенное ДУ II порядка относительно функции
- обыкновенное ДУ II порядка относительно функции 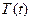 , линейное, однородное, с постоянными коэффициентами
, линейное, однородное, с постоянными коэффициентами
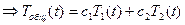 , где
, где 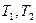 - ФСЧР.
- ФСЧР.
Характеристическое уравнение:
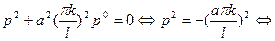
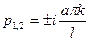 - комплексно-сопряженные корни.
- комплексно-сопряженные корни.
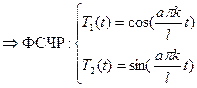
 Общее решение:
Общее решение:
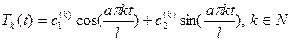
Получили счетное количество функций, констант. Получено также счетное число общих решении системы (2).
5. Перемножением функций 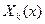 и
и 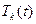 при
при 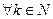 , получим счетное множество функций
, получим счетное множество функций 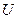 по формуле (1):
по формуле (1):
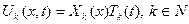
Каждая из этих функций 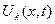 удовлетворяет ДУЧП в исходной задаче и нулевым граничным условиям при
удовлетворяет ДУЧП в исходной задаче и нулевым граничным условиям при 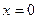 и
и 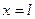 . Следовательно, в исходной остаются невыполненными только начальные условия для функции
. Следовательно, в исходной остаются невыполненными только начальные условия для функции 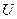 .
.
С другой стороны, найденные функции 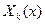 и
и 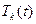 имеют несколько счетных наборов пока произвольных коэффициентов. Чтобы подобрать все эти коэффициенты так, чтобы удовлетворялись начальные условия, образуем ряд из функций
имеют несколько счетных наборов пока произвольных коэффициентов. Чтобы подобрать все эти коэффициенты так, чтобы удовлетворялись начальные условия, образуем ряд из функций 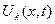 :
:
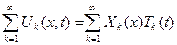
Далее будем предполагать, что этот ряд сходится при 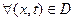 , причем сходится равномерно, так что его сумма является непрерывной функцией в области
, причем сходится равномерно, так что его сумма является непрерывной функцией в области 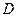 и дважды дифференцируемой через почленное дифференцирование слагаемых ряда.
и дважды дифференцируемой через почленное дифференцирование слагаемых ряда.
Обозначим сумму слагаемых ряда через 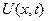
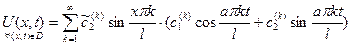
Получен функциональный ряд, членами которого являются функции от двух переменных 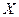 и
и 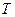 , и ряд имеет два набора произвольных коэффициентов:
, и ряд имеет два набора произвольных коэффициентов:
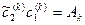
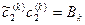
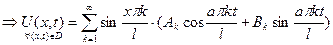 (5)
(5)
Эта функция 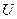 удовлетворяет исходному ДУЧП и нулевым граничным условиям, т.к. им удовлетворяет каждый член ряда. Далее будем (искать) находить
удовлетворяет исходному ДУЧП и нулевым граничным условиям, т.к. им удовлетворяет каждый член ряда. Далее будем (искать) находить 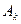 и
и 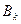 такими, чтобы удовлетворялись исходные условия поставленной задачи.
такими, чтобы удовлетворялись исходные условия поставленной задачи.
6. Определение коэффициентов 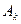 и
и 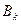
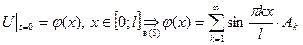
Получим представление функции 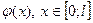 тригонометрическим рядом Фурье по синусам
тригонометрическим рядом Фурье по синусам
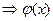 продолжена нечетным образом на промежуток
продолжена нечетным образом на промежуток 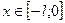 и продолжена периодически с периодом
и продолжена периодически с периодом 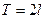 на всю числовую ось.
на всю числовую ось.
 Тогда коэффициенты
Тогда коэффициенты 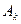 можно найти по соответствующим формулам Фурье:
можно найти по соответствующим формулам Фурье:
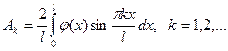 (6)
(6)
Возьмем второе начальное условие:
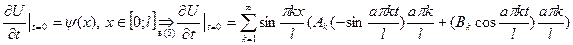
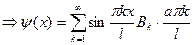
Это равенство является разложением в ряд Фурье по sin функции 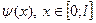 , продолженной нечетно на
, продолженной нечетно на 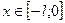 и продолженной периодически с периодом
и продолженной периодически с периодом 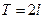 на всю числовую ось.
на всю числовую ось. 
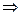 коэффициенты этого разложения также могут быть получены по формулам Фурье:
коэффициенты этого разложения также могут быть получены по формулам Фурье:
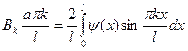
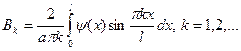 (7)
(7)
Таким образом, исходная краевая задача полностью решена, её решение получено в виде ряда (5), коэффициенты которого вычисляются по формулам (6) и (7).
Можно отметить необходимые условия на постановку задачи, чтобы ее можно было решить аналогичным образом методом Фурье.
Необходимые условия:
- ДУЧП должна быть относительно функции двух переменных и быть линейными однородными (иначе разделение переменных в нем не сделать).
- Исходная краевая задача должна быть поставлена для функции
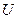 в прямоугольной области (конечной или полубесконечной), причем так, что были нулевые граничные условия на двух противоположных сторонах (иначе не сформулируется задача Штурма-Лиувилля для одной из функций)
в прямоугольной области (конечной или полубесконечной), причем так, что были нулевые граничные условия на двух противоположных сторонах (иначе не сформулируется задача Штурма-Лиувилля для одной из функций) - Функции
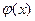 и
и 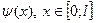 должны удовлетворять условию интегрируемости по промежутку
должны удовлетворять условию интегрируемости по промежутку 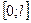 , чтобы было правомерно их разложение в ряды и чтобы вычислялись коэффициенты
, чтобы было правомерно их разложение в ряды и чтобы вычислялись коэффициенты 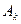 и
и 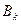 .
.
Численная реализация решения задачи.
1. Доказательство достоверности полученного решения задачи.
Полученная функция 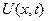 с вычисленными коэффициентами
с вычисленными коэффициентами 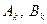 должна удовлетворять:
должна удовлетворять:
ДУЧП
Граничным условиям
Начальным условиям
1) ДУЧП – подтверждается подстановкой функции 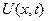 в ДУЧП
в ДУЧП
2) Граничные условия – проверяются подстановкой 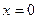 и
и 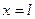 в функцию
в функцию 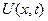
3) Начальные условия –
· проверить численно, как равенство между функциями 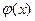 и
и 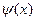 , и их разложениями в ряд Фурье, но уже с вычисленными коэффициентами;
, и их разложениями в ряд Фурье, но уже с вычисленными коэффициентами;
· для этого сначала получить визуальное совпадение графиков функций 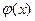 и
и 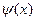 с некоторой частичной суммой
с некоторой частичной суммой 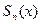 ее ряда Фурье,
ее ряда Фурье, 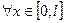 и для
и для 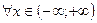 ;
;
· потом подобрать такое количество членов ряда 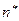 в формуле (5), чтобы равенство
в формуле (5), чтобы равенство 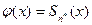 удовлетворялось с технической точностью
удовлетворялось с технической точностью 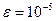 для
для 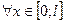 . Результаты подбора оформить в виде следующей таблицы:
. Результаты подбора оформить в виде следующей таблицы:
| 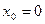
| 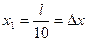
| 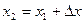
| 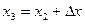
| 
| 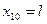
| |
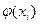
| 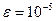
| ||||||

| 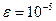
| ||||||
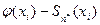
| 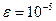
|
Подобранное здесь число 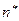 зафиксировать для табулирования функции
зафиксировать для табулирования функции 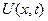 внутри области
внутри области 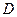 .
.
2. Протабулировать значение функции 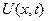 в узлах прямоугольной сетки
в узлах прямоугольной сетки 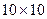 , покрывающей область
, покрывающей область  .
.
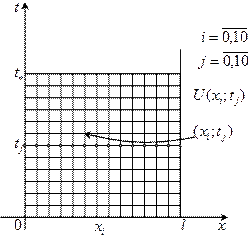
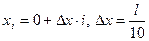
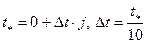 ,
,
где 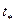 нужно подобрать так, чтобы на промежутке
нужно подобрать так, чтобы на промежутке 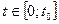 хорошо просматривалась динамика процесса (если область
хорошо просматривалась динамика процесса (если область 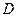 прямоугольная и конечная, то этого подбора делать не надо).
прямоугольная и конечная, то этого подбора делать не надо).
Результаты надо оформить в виде таблицы:
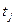 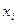
| 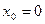
| 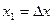
| 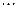
| 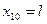
|
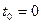
| Граничные условия для U( x, t) | Начальные условия для | Граничные условия для U( x, t) | |
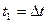
| ||||
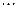
| ||||
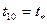
| ||||
В заголовок таблицы записать: «Табулирование функции 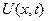 при следующих значениях управляемых параметров:
при следующих значениях управляемых параметров: 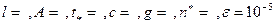 »
»
На этом этапе табулирования функции параметры можно указать произвольно.
3. Построение графика функции 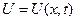 на области
на области 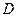 .
.
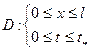
4. Провести исследование функции 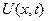 по одному или нескольким управляемым параметрам в соответствии с дополнительным заданием преподавателя.
по одному или нескольким управляемым параметрам в соответствии с дополнительным заданием преподавателя.
Дата: 2019-12-10, просмотров: 396.