Тема 3. Дифференциальные уравнения в частных производных. Решение основных задач математической физики
Тема 3. Дифференциальные уравнения в частных производных. Решение основных задач математической физики
Понятия о дифференциальных уравнениях в частных производных, об уравнениях математической физики. Постановка начальных и граничных условий.
Дифференциальное уравнение в частных производных (ДУЧП).
ДУЧП – это дифференциальное уравнение относительно функции нескольких переменных.
Если известна функция U(x,y), то ДУЧП:
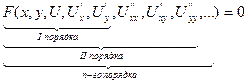
Порядок ДУЧП – это порядок старшей частной производной от неизвестной функции, входящей в данное ДУ.
Обычно рассматривают решения ДУЧП, которые описывают реальные физические (химические, биологические) процессы. В этом случае говорят о ДУЧП как об уравнениях математической физики. Основными из этих уравнений являются следующие три типа уравнений:
1. Волновое уравнение
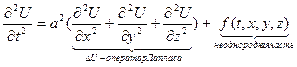
Описывает колебательные процессы функцией U(x,y,z,t), где t – время; x,y,z- координаты точек физического тела, в котором идет колебательный процесс.
Простейший вариант волнового уравнения:
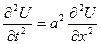
Описывает поперечные колебания струны или продольные колебания тонкого стержня без учета сопротивления среды (свободные колебания).
Неизвестная функция: U(x,t), где 
, вычисляемая по физическим характеристикам материала струны или стрежня
2. Уравнение теплопроводности:
Описывает процесс распространения тепла функцией температур U(x,y,z,t) в некотором трехмерном массиве.
, зависящая от тепло-физических характеристик материала.
Простейший вариант:
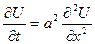
Описывает распространение тепла в тонком стержне, теплоизолированном по боковой поверхности и при отсутствии внутренних источников тепла.
3. Уравнение 
U(x,y,z)
Функция U(x,y,z) описывает различные стационарные процессы в трехмерных телах (стационарное температурное поле), положение равновесия при внешней нагрузке, процесс фильтрации вещества и т.д.).
Классификация линейных ДУЧП второго порядка
Общий вид линейного ДУЧП:
Неизвестная функция U(x,y)
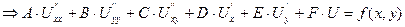(1)
1. Если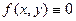 
, то ЛДУЧП (1) называется однородным.
Если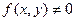 
, то ЛДУЧП (1) называется неоднородным
2. Если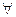 
коэффициенты 
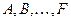являются 
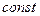по x, y, то ДЛДУЧП называется с постоянными коэффициентами
ЛДУЧП (1) делятся на ДУЧП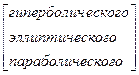 
типов
В основу этой классификации положено сходство с классификацией обычных алгебраических уравнений II степени относительно x,y и соответствующие им геометрические образы.
Алгебраическое уравнение II степени относительно x,y:
(*)
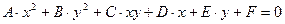Если этому уравнению соответствует реальный геометрический образ в виде кривой II порядка, то этой кривой является 
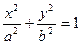- эллипс
- гипербола
или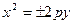 
- парабола
Характерные признаки канонических уравнений:
эллипса – обе переменные в квадратах с коэффициентами одного знака
гиперболы – обе переменные в квадратах с коэффициентами разных знаков
параболы – одна переменная в квадрате, а вторая только в первой степени
остаются устойчивыми (инвариантными) при любых линейных преобразованиях координатных осей (сдвигах, поворотах, растяжениях)
Благодаря их инвариантности (……………….) они проявляются в общем уравнении вида (*) и по аналогии переносятся на ДУЧП вида (1)
Примеры проявления классификации
1. Волновое уравнение
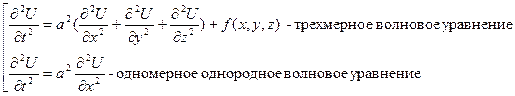
Это ДУЧП гиперболического вида
2. Уравнение теплопроводности (уравнение Фурье)
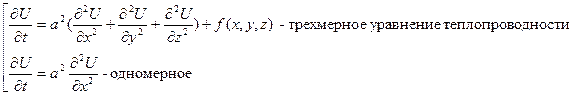
Это ДУЧП параболического вида
3. ДУЧП Пуассона или Лапласа
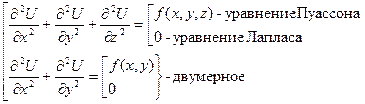
Это ДУЧП эллиптического вида
Эта классификация ДУЧП используется в построении методов их решения, в особенностях сходимости этих методов
Постановка начальных условий
Начальные условия к ДУЧП ставятся только тогда, когда неизвестная функция зависит от времени t, т.е. эта неизвестная функция описывает какой-то нестационарный физический процесс. Начальные условия характеризуют этот процесс в начальный момент времени.
Количество начальных условий определяется так же, как в задаче Коши для обыкновенных ДУ: количество начальных условий будет совпадать с порядком старшей производной по времени в ДУЧП.
Примеры:
1. Волновое уравнение:
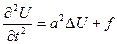
Начальные условия:
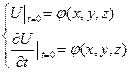
Смысл начальных условий.
Функция 
- это смещение точки (x,y,z) от положения равновесия в любой момент времени t.
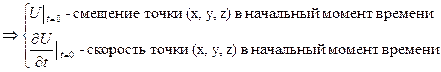
2. Уравнение теплопроводности
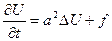
Начальное условие: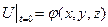 
Смысл начального условия.
Функция - температура в точке (x,y,z) неравномерно нагретого тела в любой момент времени t.
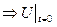- температура точек (x,y,z) в начальный момент времени.
3. Уравнение Лапласа (Пуассона)
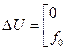
Начальных условий не нужно, т.к. неизвестная функция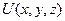 
не зависит от времени и описывает установившийся во времени процесс.
Граничные условия к ДУЧП
Граничные условия к ДУЧП – это условия на неизвестные, описывающие ее значения на границе физического тела, в котором идет процесс, описываемый неизвестной функцией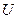 
.
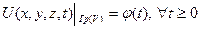
Граничные условия бывают трех видов.
1. Граничные условия Дирихле
2. Граничные условия Неймана
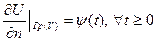
n – нормаль у границе области V в ее точке.
3. Смешанные граничные условия.
Это когда на одной части границы заданы условие Дирихле, а на другой – условие Неймана.
Постановка к ДУЧП начальных и граничных условий однозначно должна определять неизвестную функцию 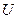в этом ДУЧП.
Дата: 2019-12-10, просмотров: 300.
