В работах Летова А.М. [4] терминальные задачи управления формулировались как задачи оптимизации функционала вида

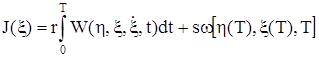,                                  (3.1)

где W, w – некоторые неотрицательные и достаточно гладкие функции своих аргументов, а r, s – неотрицательные числа. Функции h, x описывают движение возмущенное по Ляпунову. Второе слагаемое функционала (3.1) характеризует меру отклонения систем от заданного конечного состояния в момент времени t = T.

Первое слагаемое налагает на управление дополнительное требование: помимо перевода объекта в заданное конечное состояние оно должно обеспечить ему некоторые полезные свойства. Относительно выбора вида функций W и w обычно не делается никаких строгих рекомендаций.

Если в (3.1) положить r = 0, то система оптимизируется по функционалу

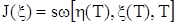.                                                               (3.2)

Отметим, что в случае использования функционала (3.2) задача вырождается в чисто краевую, так как единственной целью управления становится соблюдение конечных условий. В этом случае никаких дополнительных требований фазовой траектории не предъявляется.

В 1968 г. Н.Н. Красовский [5] отметили значительные трудности, возникающие при решении краевых задач в вариационной постановке. Для решения краевых задач применительно к задачам управления самолетом он предложил способ минимизации следующего функционала, который обеспечивает не только перевод объекта в заданное состояние, но и хорошее качество этого перевода

.      

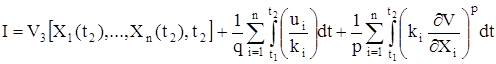Здесь p, q – положительные числа, удовлетворяющие соотношению 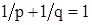, и такие, что zp, zq, – четные функции z; ki – заданные вещественные числа; V=V(X1, X2, …, Xn, t) – решение уравнения  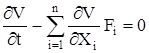при граничном условии 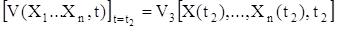. Полученные законы управления обеспечивали вывод самолета на взлетно-посадочную полосу (ВПП) без перерегулирования.

Работа [6] посвящена синтезу оптимального управления для линейного объекта 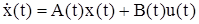. Критерием качества служит функционал

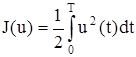,                                                                      (3.3)

минимизирующий энергетические затраты на управление.

В качестве примера решена задача вывода ракеты в течение времени T в заданную точку с координатой xf1 и конечной скоростью xf2. Управляющая функция имеет вид

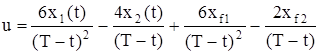. (3.4)

Здесь u – заданное ускорение объекта; T – требуемое время выполнения задачи; x1(t), x2(t) – текущие значения координаты и скорости объекта; xf1, xf2 – конечные значения координаты и скорости.

Полученный закон управления является замкнутым и переводит объект в течение времени T из произвольной начальной точки фазовой плоскости в произвольную конечную. Однако этот закон обладает особенностью в конечной точке: при t = T знаменатель в (3.4) обращается в нуль. Эта особенность закона затрудняет его практическое применение.

Описанное в приведенных работах направление базируется на теории оптимизации квадратичных функционалов. Ввиду этого все рассмотренные подходы отличает повышенная трудность решений. В тоже время в постановках задач отмечаются следующие особенности. У большинства авторов невязки по фазовым координатам в конечный момент времени T включены в функционал. Зачастую кроме этих невязок функционал ничего другого не содержит. Следовательно, в этих случаях достигается единственная цель – перевод объекта в конечное фазовое состояние. Никакие дополнительные требования к фазовой траектории не предъявляются. Таким образом, сложные вариационные методы применяются здесь лишь как средство решения краевой задачи.

В большинстве рассмотренных работ управляемый объект переводится в начало координат фазового пространства. Так как при этом заданные конечные значения фазовых координат равны нулю, то в окончательные выражения для управлений они не входят. Нужно особо подчеркнуть, что перевод фазовой точки в начало координат или в произвольную точку фазового пространства – не одно и то же. Конечные значения фазовых координат входят в формулы для управлений со своими весовыми коэффициентами (3.4) и определение этих коэффициентов является составной частью задачи синтеза.

В некоторых работах требуется в течение заданного времени Т < Tопт перевести фазовую точку на возможно близкое расстояние к началу координат. Так как в этом случае конечное фазовое состояние объекта неизвестно, то оно также не входит в окончательные формулы.

Найденные оптимальные управления, как правило, принадлежат классу кусочно-непрерывных функций времени, мгновенно переключающихся с одного ограничения на другое.

Таким, образом, построенные на этой основе САУ не имели, бы обратных связей и не могли бы противодействовать внешним возмущениям. Кроме того, переключательные управляющие функции недопустимы для значительного числа управляемых объектов из соображений безопасности, прочности и т.д. По этой причине они не нашли достаточного практического применения в технике.

Оценивая данное направление в целом, следует заключить, что оно не дало пока приемлемых для инженерной практики решений. И может быть применено лишь в некоторых ограниченных случаях.