Как указывалось выше, вариационная постановка задачи поиска терминального управления используется лишь с единственной целью – свести эту задачу к известному классу и применить достаточно разработанный, хотя и сложный метод решения.

Очевидно, что в этих случаях вариационный метод используется лишь как инструмент для решения краевой задачи. При наличии простых специальных методов решения краевых задач от вариационной постановки можно было бы отказаться ввиду математических сложностей, к которым она приводит. Вариационные методы должны использоваться там, где они действительно необходимы.

Иное направление в решении терминальной проблемы дает поиск управлений в заданном классе непрерывных функций или поиск управлений, реализующих заданное движение системы.

Невариационный, или чисто терминальный, подход был впервые предложен Грином в 1961 г. для управления мягкой посадкой космического аппарата [7]. Поиск управления, представляющего собой заданное ускорение объекта, производился в классе постоянных во времени функций u = Со, которые реализуют равномерно замедленное движение. При переходе к замкнутой форме этот закон принимает вид

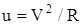,                                                                                 (3.5)

где u – заданное ускорение аппарата; V – текущая вертикальная скорость аппарата; R – оставшееся до посадочной площадки расстояние. Однако этот закон имеет существенный недостаток: в момент приземления знаменатель в (3.5) обращается в нуль. Если устранить эту особенность в конечной точке, то закон примет вид

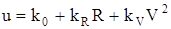.                                                                (3.6)

Требуемое время выполнения задачи в закон (3.6) не входит, поэтому он разомкнут по времени. Следовательно, время перевода объекта из начальной точки в конечную задавать нельзя. Однако его можно вычислить по формуле

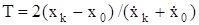,                                                          (3.7)

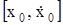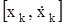где  и  – соответственно начальное и конечное фазовые состояния объекта.

Закон управления (3.4), реализующий движение с линейно-изменяющимся ускорением,

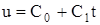                                                                               (3.8)

был получен в [8] и использовался для посадки вертикально взлетающего самолета.

Необходимо подчеркнуть, что этот закон получен не путем минимизации функционала (3.3), а совершенно иным методом. Управление искалось в классе линейных функций (3.8), а неизвестные коэффициенты Со и С1 определялись из конечных условий.

Закону (3.4) также присуща особенность в конечной точке: при t = Т его знаменатель обращается в нуль. В [9] предложен способ устранения особенности, реализующий погоню управляемого объекта за ведущей фазовой точкой на постоянном временном интервале. В результате (3.4) преобразуется к виду

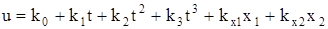,                                (3.9)

где коэффициенты k0, k1, k2, k3 зависят от начального и конечного фазовых состояний объекта, а также заданного времени перехода Т; коэффициенты kx1, kx2 зависят от временного интервала DТ; x1, x2, t – текущие значения фазовых координат объекта и времени, отсчитываемые с начала момента движения.

Закон (3.9) является замкнутым по времени, так как позволяет задавать требуемое время перевода объекта из начального состояния в конечное.

Оценивая в целом описанное в данном разделе направление, следует отметить присущую ему простоту алгоритмов и методов.