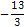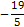Пример 1. Найти наибольшее из значений z, для которых существуют числа x , y, удовлетворяющие уравнению
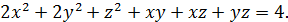
Решение.
Так как нужно найти наибольшее значение z , то в левой части равенства будем последовательно выделять полные квадраты, сначала относительно x , затем относительно y . (Конечно, можно сначала выделить полный квадрат относительно y, затем относительно x).
Итак,

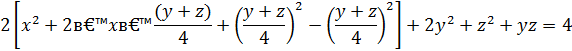
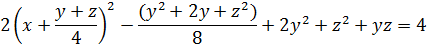
Обозначим 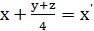 и соберем подобные члены
и соберем подобные члены
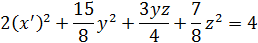
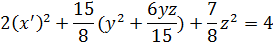
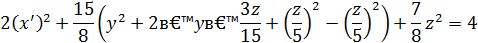
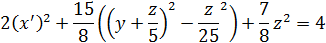
Обозначим 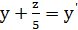
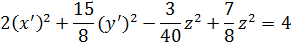
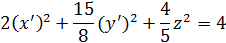
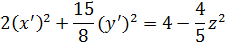
Так как левая часть последнего равенства неотрицательна, то правая часть должна быть неотрицательной:
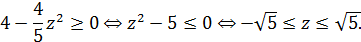
Итак, необходимо 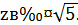 Покажем, что можно найти такие x , y , при которых
Покажем, что можно найти такие x , y , при которых 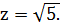 Если
Если 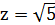 , то
, то
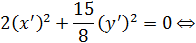
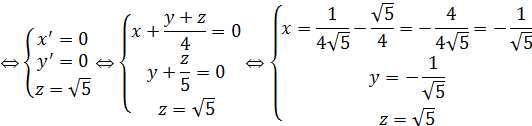
Ответ. 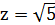
Пример 2. Числа x , y , z таковы, что 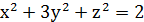 . Какое наибольшее значение может принимать выражение
. Какое наибольшее значение может принимать выражение 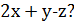
Пример 2 мы сведем к примеру 1.
Пусть значение
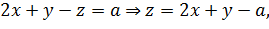
подставляя это выражение для z в уравнение, получим:
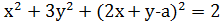 .
.
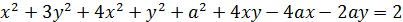
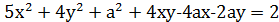 (1)
(1)
Теперь задача формулируется так: найти наибольшее значение а, для которого существуют числа x , y , удовлетворяющие уравнению (1).
Опять выделяя полные квадраты, сначала относительно х, затем относительно у, получаем:
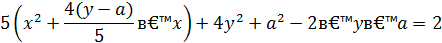
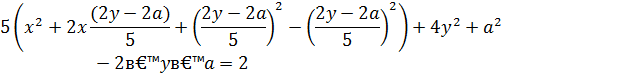
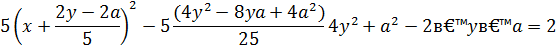
Обозначим 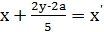 .
.
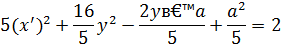
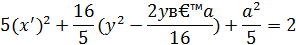
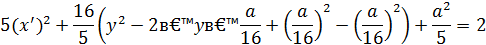
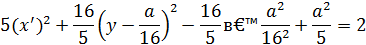
Положим 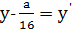
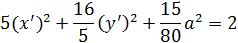
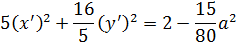
Так как левая часть последнего равенства больше или равна нулю, то и правая часть должна быть неотрицательна, то есть
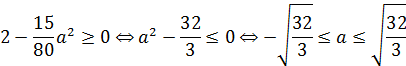
Решая систему
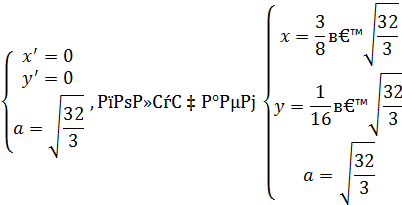
Ответ. Наибольшее значение а = 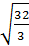 .
.
Пример 3. Найти все значения а, при каждом из которых существует единственная пара целых чисел x , y, удовлетворяющих уравнению 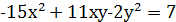 и двум неравенствам
и двум неравенствам 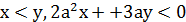
Решение.
1) Будем рассматривать левую часть равенства, как, например, квадратный трехчлен относительно 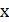 и попытаемся разложить его на множители.
и попытаемся разложить его на множители.
Для этого воспользуемся теоремой 4. Согласно этой теореме, нужно найти корни уравнения: 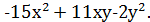
Его дискриминант 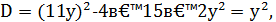 и тогда
и тогда
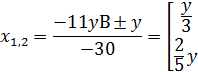
Теперь 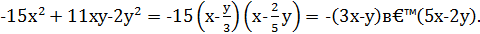
Тогда равенство 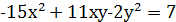 можно переписать в виде:
можно переписать в виде:
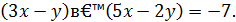
Так как мы ищем только пары целых чисел ( x , y ), то числа
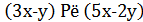 тоже целые.
тоже целые.
Целыми делителями числа 7 являются числа 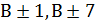 и только они. Поэтому данное уравнение равносильно совокупности четырех систем:
и только они. Поэтому данное уравнение равносильно совокупности четырех систем:
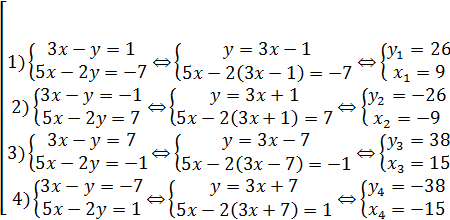
2) Установлено, что уравнение 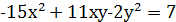 имеет ровно четыре пары целых решений. Неравенству x < y, удовлетворяют только две пары: (9; 26) и (15;38).
имеет ровно четыре пары целых решений. Неравенству x < y, удовлетворяют только две пары: (9; 26) и (15;38).
3) Выясним при каких а эти две пары из пункта 2) удовлетворяют условию:  .
.
(9; 26): 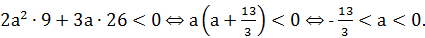
(15; 38): 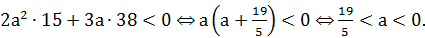
|
 | |||||||||||||
|
|
|
| ||||||||||
Из чертежа видно, что для 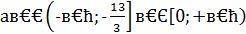 задача не имеет целых решений; для
задача не имеет целых решений; для 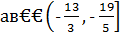 - лишь одна целая пара (9; 26) удовлетворяет всем условиям; при
- лишь одна целая пара (9; 26) удовлетворяет всем условиям; при 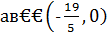 имеются две пары целых чисел, удовлетворяющих задаче (9; 26) и (15; 38).
имеются две пары целых чисел, удовлетворяющих задаче (9; 26) и (15; 38).
Ответ. 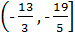 .
.
Дата: 2019-12-10, просмотров: 370.