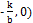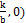Теоретическая значимость исследования состоит в систематизации и обобщении данной темы. Теоретически значимым также являются проведённый анализ методико-педагогической литературы по теме «Линейные и квадратичные зависимости».
Практическая значимость работы заключается в возможности использования в решении задач доказанных формул и утверждений. При этом может быть использована выполненная подборка задач, для которых метод выделения полного квадрата является рациональным. Материалы этой работы могут быть полезны учителям школ и студентам педагогических институтов.
Структура работы.
Работа состоит из введения, трёх глав, заключения и приложения, включает страниц машинописного текста и имеет список литературы из наименований.
Глава 1. Линейная зависимость и связанные с ней уравнения и неравенства
Линейная функция
Определение. Функция, задаваемая формулой у = k ·х + b , называется линейной.
В школьной программе доказывается, что графиком линейной функции на плоскости является прямая, и обратно, что любая прямая на плоскости есть график некоторого линейного уравнения a· x + b · y + c = 0.
Уравнение у = k ·х + b называется уравнением прямой с угловым коэффициентом k
 | |||
 | |||
|


|
|
 | |||
| |||
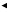
|
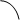

 |
|
|
|
|
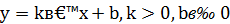
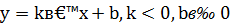
Приведенные выше два рисунка иллюстрируют связь параметров k и b с особенностями расположения прямой в декартовой системе координат. В частности, число k = tg α называется угловым коэффициентом прямой.
В данном случае 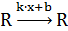 . Если k = 0, то
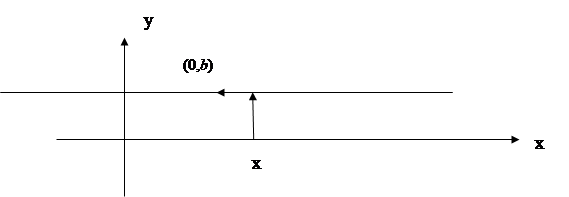
. Если k = 0, то 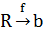 , линейная функция постоянна и задает прямую, параллельную оси ОХ и | проходящую через точку (0,b) на оси OY.
, линейная функция постоянна и задает прямую, параллельную оси ОХ и | проходящую через точку (0,b) на оси OY.
Перечислим основные свойства линейной функции.
1. Ее областью определения является множество R.
2. Если k 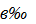 0 , то множеством значений линейной функции также является множество R, если k = 0, то множество значений — одноточечное множество b .
0 , то множеством значений линейной функции также является множество R, если k = 0, то множество значений — одноточечное множество b .
3. Если k > 0, то 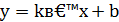 - монотонно возрастающая функция на R, если k < 0, то
- монотонно возрастающая функция на R, если k < 0, то 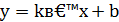 - монотонно убывает на R.
- монотонно убывает на R.
4. Если b = 0, то 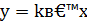 - нечетная функция, у = b - четная функция; если же
- нечетная функция, у = b - четная функция; если же 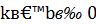 , то
, то 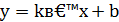 не является четной или нечетной функцией.
не является четной или нечетной функцией.
Рассмотренные выше случаи не позволяют задать прямую, параллельную оси OY. Поэтому условимся, что уравнение х=х0 задает
множество всех точек вида (х0, у), где у 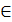 R, то есть задает прямую
R, то есть задает прямую
параллельную оси OY и проходящую че рез точку (хо, 0) на оси ОХ.
Чтобы построить прямую, задаваемую уравнением 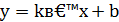 , достаточно найти две точки (х0, у0) и (х1, у1), удовлетворяющие этому уравнению: у0 = k
, достаточно найти две точки (х0, у0) и (х1, у1), удовлетворяющие этому уравнению: у0 = k 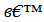 х0 + b ; у1 = k
х0 + b ; у1 = k 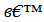 х1 + b и провести через них искомую прямую.
х1 + b и провести через них искомую прямую.
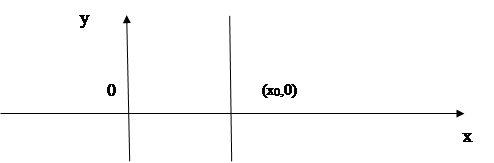
Дата: 2019-12-10, просмотров: 362.