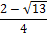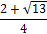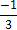Опираясь на иллюстрации, сформулируем следующее правило решения квадратных неравенств:
| Неравенство | Ответ |
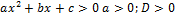
| 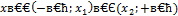
|

| 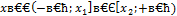
|
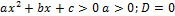
| 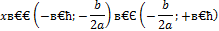
|
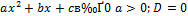
| 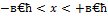
|
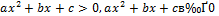
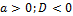
| 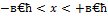
|
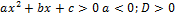
| 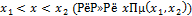
|
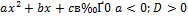
| 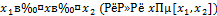
|
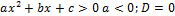
| Нет решений (или 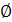 ) )
|
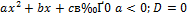
| x = 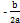
|
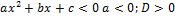
| 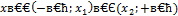
|
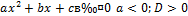
| 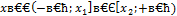
|
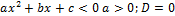
| 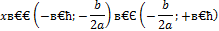
|
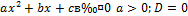
| x = 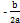
|
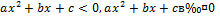
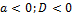
| 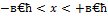
|
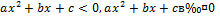
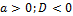
| Нет решений (или 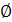 ) )
|
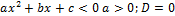
| Нет решений (или 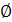 ) )
|
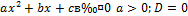
| x = 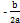
|
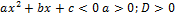
| 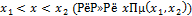
|
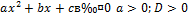
| 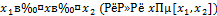
|
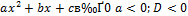
| Нет решений (или 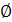 ) )
|
Разложение квадратного трехчлена на линейные множители
Теорема 4.
1) Если D > 0, то 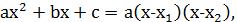

2) Если D = 0, то 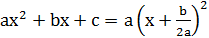 .
.
3) Если D < 0, то 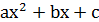 нельзя разложить на линейные множители, используя в качестве коэффициентов этих линейных множителей вещественные числа.
нельзя разложить на линейные множители, используя в качестве коэффициентов этих линейных множителей вещественные числа.
Пример 1. 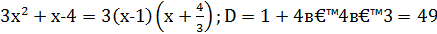
Пример 2. 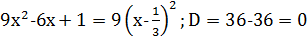
Пример 3. 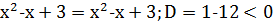 .
.
Укажем и другие связи между корнями и коэффициентами квадратного трехчлена.
Теорема 5. (Виета)
Если 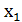 ,
, 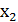 - вещественные корни уравнения
- вещественные корни уравнения 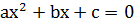 , то
, то
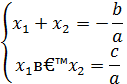
Теорема 6. (Обратная теорема Виета)
Если 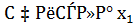 ,
, 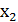 удовлетворяют условиям системы:
удовлетворяют условиям системы:

то 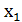 ,
, 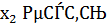 корни уравнения
корни уравнения 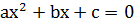 .
.
Часто встречаются задачи, в которых требуется выяснить взаимное расположение какого-либо числа и корней квадратного трехчлена на числовой оси.
Следующая теорема позволяет существенно упростить решение подобного рода задач. Отметим, что для уменьшения числа разбираемых различных случаев мы переходим к рассмотрению приведенного квадратного уравнения, которое получается после деления всех коэффициентов уравнения на старший коэффициент a.
Теорема 7.
Пусть 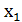 ,
, 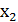 - вещественные корни уравнения
- вещественные корни уравнения 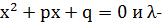 число.
число.
| Для того, чтобы | Необходимо и достаточно |
I. 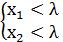
| 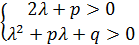
|
II. 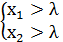
| 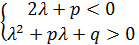
|
III. 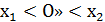
| 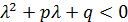
|
Место для формулы.
Докажем случай 1.
Необходимость.
Пусть 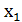 ,
, 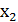 - вещественные корни уравнения
- вещественные корни уравнения 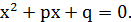
Если 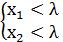 , то необходимо выполняются условия
, то необходимо выполняются условия
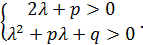
Доказательство.
Так как по условию
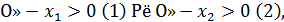
то сложив (1) и (2) получим 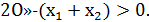 По теореме Виета
По теореме Виета 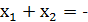 p, то есть
p, то есть 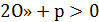 , что и требовалось доказать.
, что и требовалось доказать.
Перемножив (1) и (2), получим
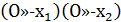 >0
>0 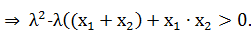
Воспользовавшись теоремой Виета:
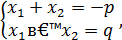
получим 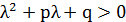 , что и требовалось доказать.
, что и требовалось доказать.
Достаточность.
Пусть 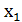 ,
, 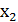 - вещественные корни уравнения
- вещественные корни уравнения 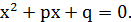
Для того, чтобы оба корня были меньше числа 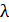 , достаточно, чтобы выполнялась следующая система неравенств:
, достаточно, чтобы выполнялась следующая система неравенств:
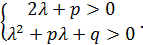
Доказательство.
По условию, справедлива система:
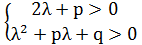 (1)
(1)
Вновь воспользуемся теоремой Виета
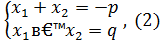
тогда система (1) примет вид:
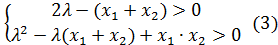
Переписав систему (3) в другом виде, получим систему (4):
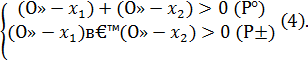
Неравенство (б) означает, что числа 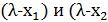 ) имеют одинаковые знаки, а неравенство (а), что оба эти числа положительны, то есть
) имеют одинаковые знаки, а неравенство (а), что оба эти числа положительны, то есть
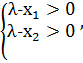 иначе говоря
иначе говоря 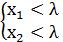 , что и требовалось доказать.
, что и требовалось доказать.
Задачи
Обозначим через 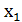 ,
, 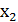 корни квадратного трехчлена (a-1)
корни квадратного трехчлена (a-1) 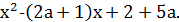 Найти все а, при которых оба корня больше 1.
Найти все а, при которых оба корня больше 1.
Решение.
а) Если а=1, то уравнение -3x + 7 = 0 имеет только один корень, поэтому 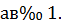
б) При 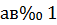 воспользуемся пунктом II теоремы 7, который позволяет сразу записать:
воспользуемся пунктом II теоремы 7, который позволяет сразу записать:
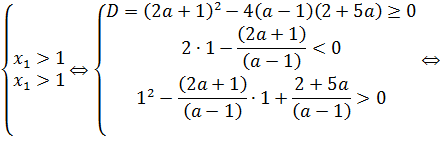
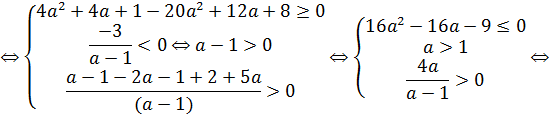
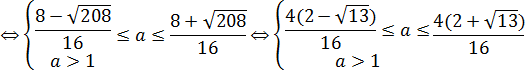
 | |||||||||
|
|
| |||||||
Ответ.  .
.
2. Найти все значения 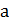 , при которых корни уравнения
, при которых корни уравнения 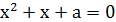 больше
больше 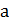 .
.
Решение.
Воспользовавшись пунктом II теоремы 7 получаем:
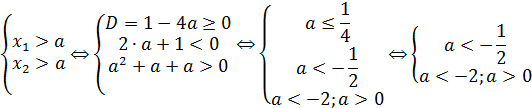

Ответ. a < -2.
3. Найти все значения 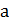 , при которых оба корня квадратного уравнения
, при которых оба корня квадратного уравнения
 будут меньше 1.
будут меньше 1.
Решение.
Уравнение будет квадратным только если 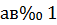 . В этом случае оно равносильно уравнению:
. В этом случае оно равносильно уравнению:
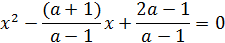
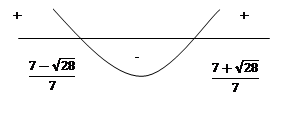
Согласно пункту 1 теоремы 7 получаем, что
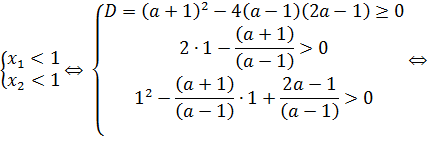
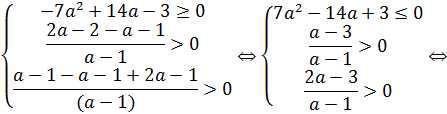
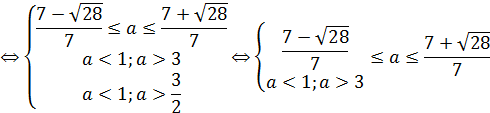
 | ||||||||||||||
 | ||||||||||||||
|
| |||||||||||||
| ||||||||||||||
 | ||||||||||||||
| ||||||||||||||
| ||||||||||||||
| ||||||||||||||
|










Ответ. 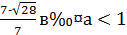 .
.
Иногда применение теоремы 7 вызывает трудности, так как возникают неравенства третьей или более высокой степени. Тогда, скорее всего, можно выражения для корней исходного квадратного трехчлена получить в виде рациональных функций параметра.
Иными словами:
Если применение теоремы 7, вызывает алгебраические трудности, стоит проверить, не является ли дискриминант рассматриваемого квадратного уравнения полным квадратом. Если дискриминант является полным квадратом, то нужно попытаться выписать выражения для корней и продолжить решение задачи.
4. При каких значениях а все корни уравнения
3a 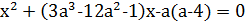 удовлетворяют условию
удовлетворяют условию 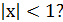
1) Заметим, что если 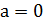 , то уравнение имеет единственный корень
, то уравнение имеет единственный корень 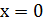 , и число 0 удовлетворяет условию задачи.
, и число 0 удовлетворяет условию задачи.
2) Если 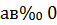 , то
, то 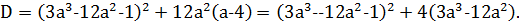
Заменим  , тогда
, тогда
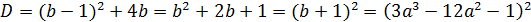
- данное выражение есть полный квадрат! Теперь легко вычислить:

Условие задачи будет выполнено, если справедлива система:
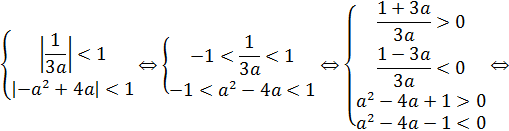
 | ||||||||||||
| ||||||||||||
 | ||||||||||||
|
| |||||||||||
 | ||||||||||||
|
|
|

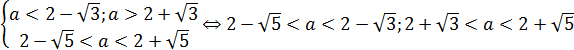
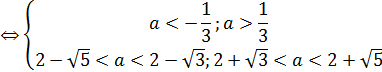
Сравним числа из промежуточных ответов:
пусть 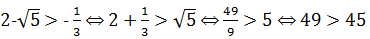 верно;
верно;
пусть 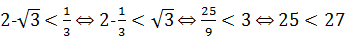 верно.
верно.
 |
Пересечение ответов является множество:
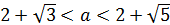
Ответ. 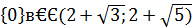
Дата: 2019-12-10, просмотров: 359.