1. Создание проблемной ситуации, мотивирование и постановка цели:
- Посмотрите, а кто же нас здесь дожидается? (Показ игрушек или иллюстрации – персонажи мультфильма «38 попугаев»). Мартышка, Слоненок и Попугай хотят помочь своему лучшему другу Удаву, ведь он не знает, какой он длины, не понимает, как ему измерить свою длину.
- Ребята, мы им поможем? (дети соглашаются)
- Посмотрите, как Удав обрадовался! Он наконец-то узнает свою длину!
2. Выдвижение детьми предположений о результатах , их обоснование:
- Вспомним мультфильм про Удава! Кем или чем герои мультфильма измеряли Удава? (Попугаем, Мартышкой, Слонёнком).
- Какой длины был Удав, когда его измерял Слонёнок? (2 Слонёнка!)
- Какой длины был Удав, когда его измеряла Мартышка? (5 мартышек!)
- А в Попугаях длина удава? (38 Попугаев!)
- Совсем запутался бедный Удав, ничего не понимает! Почему же так получилось, почему результат измерения его длины всегда разный?
Дети высказывают предположения!
3. Проведение эксперимента:
- Ребята, посмотрите, здесь полоски разной длины и цвета. Что мы можем сказать об их длине? ( Они все разные по длине!)
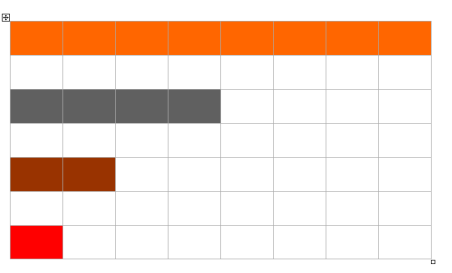
- Разложите эти полоски от самой длинной до самой короткой.
- Какая полоска самая длинная? (Оранжевая!) А какая самая короткая? (Красная!)
- Представьте, что оранжевая полоска - это Удав, серая – это Слоненок, коричневая - это Мартышка, а красная - это Попугай.
- Мы будем измерять Удава в Слонах, в Мартышках и в Попугаях. Как же мы будем это делать?
Дети рассказывают:
- Берем серую условную мерку (Слонёнка) и накладываем ее на край коричневой полоски (Удав), делаем метку карандашом, откладываем одну счётную палочку. Теперь от того места, где отметили, снова кладём край условной мерки и снова отмечаем карандашом, откладываем счётную палочку, и так до конца.
Далее дети самостоятельно измеряют длину удава в «Слонах», «Мартышках» и «Попугаях».
4. Фиксация результатов, их обсуждение с помощью педагога:
- Что делали?
- Что получили?
- Почему?
5. Общий вывод (формулирует педагог на основе высказывания детей):
Наводящими вопросами воспитатель подводит детей к выводу об обратной функциональной зависимости между результатом измерения и величиной мерки.
- Чем длиннее мерка, тем меньше результат измерения!
- Чем короче мерка, тем больше результат измерения!
- Ребята, посмотрите, какой стал удав довольный, веселый. Он очень рад, что вы ему помогли, объяснили, что его длина зависит от того, кто из друзей помогает её измерять.
6. Самостоятельная экспериментально - исследовательская деятельность:
В развивающую среду группы вносятся различные линейные величины (шарфики, коврики, дощечки и т.д.) и УМ для их измерения разной длины и осознания обратной функциональной зависимости между результатом измерения и величиной условной мерки
ПРИМЕЧАНИЕ
Если Вы заранее подготовите и вложите в Портфолио наглядный дидактический материал, например, вырезанные условные мерки или персонажей мультфильма соответствующего размера, Ваш ответ на экзамене будет выглядеть эффектно!
ВОЗМОЖНЫЙ ДОПОЛНИТЕЛЬНЫЙ ВОПРОС
- Предложите варианты экспериментально-исследовательской деятельности для осознания детьми прямой функциональной зависимости между объектом и результатом измерения на основе мультфильма «38 попугаев»
- Мы можем измерять в попугаях все остальные персонажи мультфильма. Чем длиннее персонаж, тем больше попугаев получилось! Чем длиннее объект, тем больше результат измерения!
______________________________________________________________________________
ВОПРОС 7
Предложить варианты игровых упражнений для осознания детьми старшего дошкольного возраста прямой и обратной функциональной зависимости между объектом, средством измерения и результатом измерения.
ОТВЕТ НА ЭКЗАМЕНЕ
ВЕЛИЧИНА - одно из основных математических понятий, отражающее идею измерения или исчисления объектов окружающего мира.
Познакомив детей с понятием величины, в старшем дошкольном возрасте мы начинаем знакомить их с понятием измерения величин.
Измерить - это значит дать численную характеристику величине. C этой целью мы используем условные мерки – предметы определённой величины, меньшей, чем измеряемый объект.
Объект – измеряемая величина.
Средство измерения – величина, принятая за единицу измерения, условная мерка.
Результат измерения – количество условных мерок.
Использование УМ позволяет детям сделать выводы:
1. Чем больше величина, тем больше результат измерения. Это - прямая функциональная зависимость между объектом и результатом измерения. (Для сравнения величин необходимо их измерять одинаковыми мерками).
Я предлагаю варианты экспериментально-исследовательской деятельности для осознания детьми прямой функциональной зависимости между объектом и результатом
– для линейных величин (показ красивых картинок с пояснениями)
- для сыпучих веществ (показ красивых картинок с пояснениями)
- для жидких веществ (показ красивых картинок с пояснениями)
2. Чем больше условная мерка, тем меньше результат измерения и наоборот. Это - обратная функциональная зависимость между средством и результатом измерения. (Измеряемый объект используется только один!)
Я предлагаю варианты экспериментально-исследовательской деятельности для осознания детьми обратной функциональной зависимости между условной меркой и результатом измерения
– для линейных величин (показ красивых картинок с пояснениями)
- для сыпучих веществ (показ красивых картинок с пояснениями)
- для жидких веществ (показ красивых картинок с пояснениями)
_____________________________________________________________________
ВОПРОС 8
Предложить варианты развивающих игр математической направленности для развития логического мышления и закрепления представлений о форме предметов и о геометрических фигурах у детей старшего дошкольного возраста.
ОТВЕТ НА ЭКЗАМЕНЕ

Я предлагаю следующие варианты развивающих игр математической направленности для развития логического мышления и закрепления представлений о форме предметов и о геометрических фигурах у детей старшего дошкольного возраста.
1. Что лишнее?
2. Найди отличие?
3. Найди одинаковое!
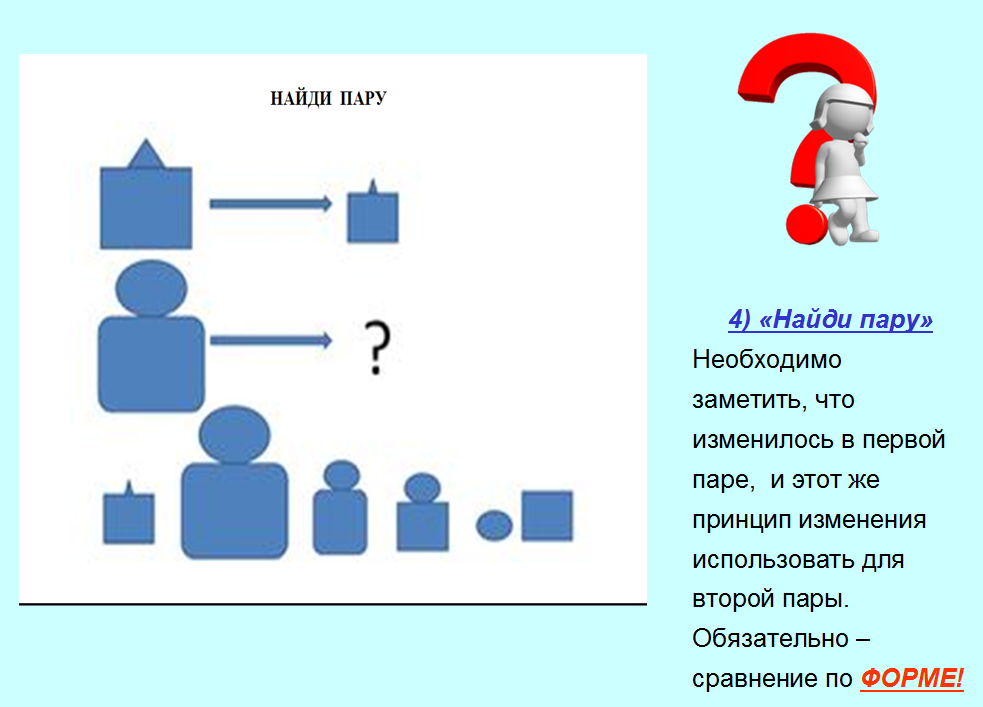
4. Найди пару!
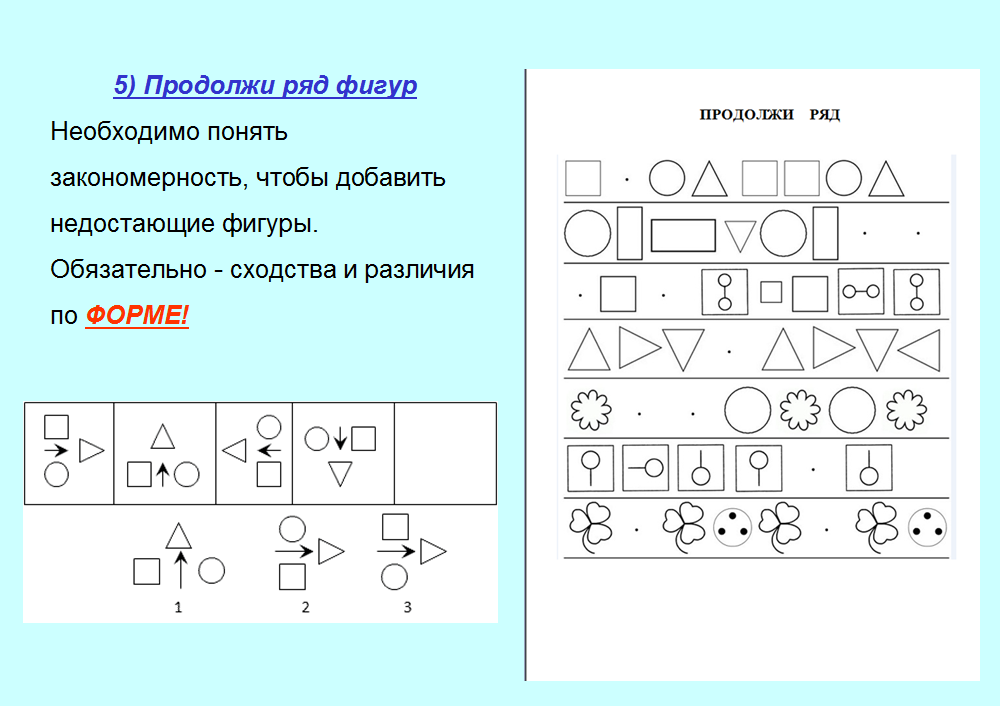
5. Продолжи ряд фигур!
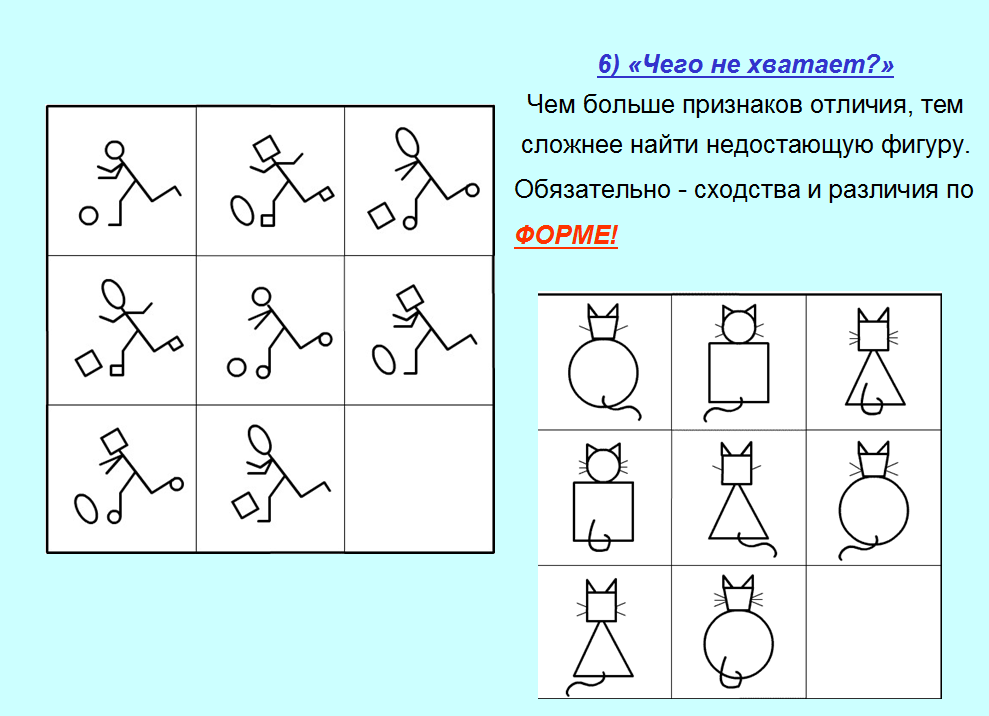
5. Чего не хватает?
Примеры развивающих игр математической направленности:
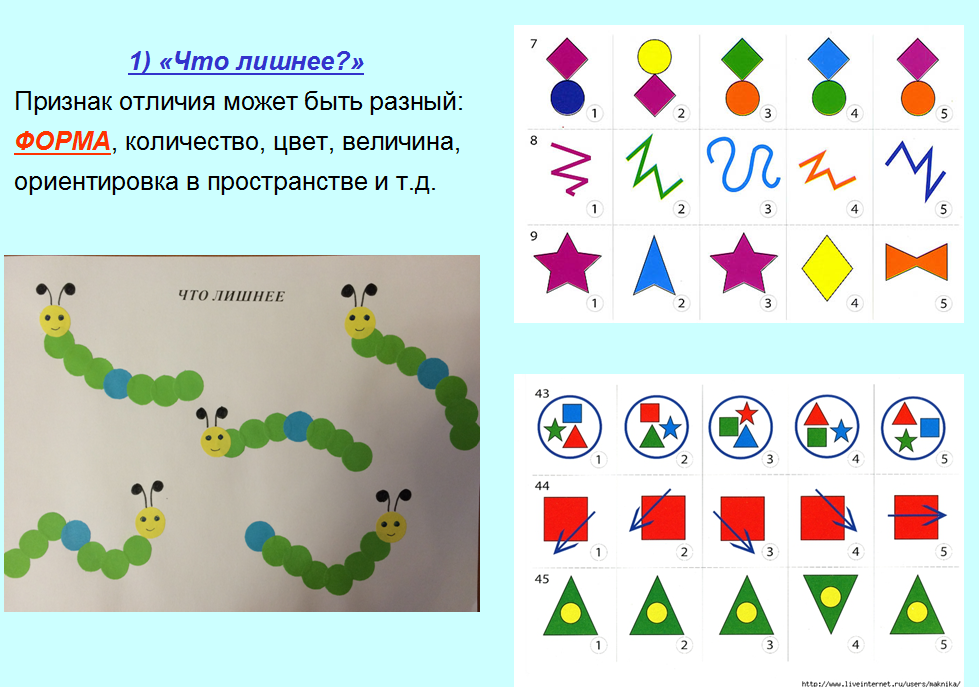
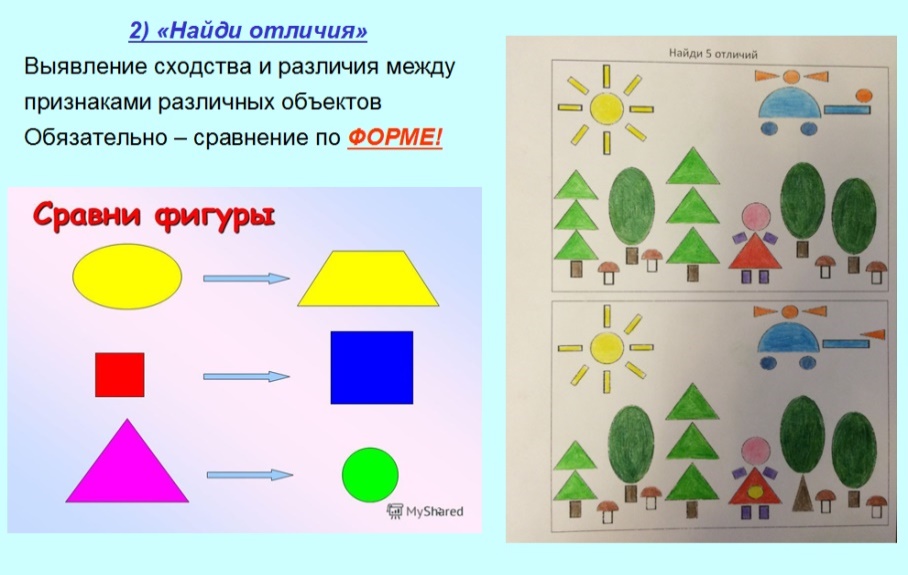
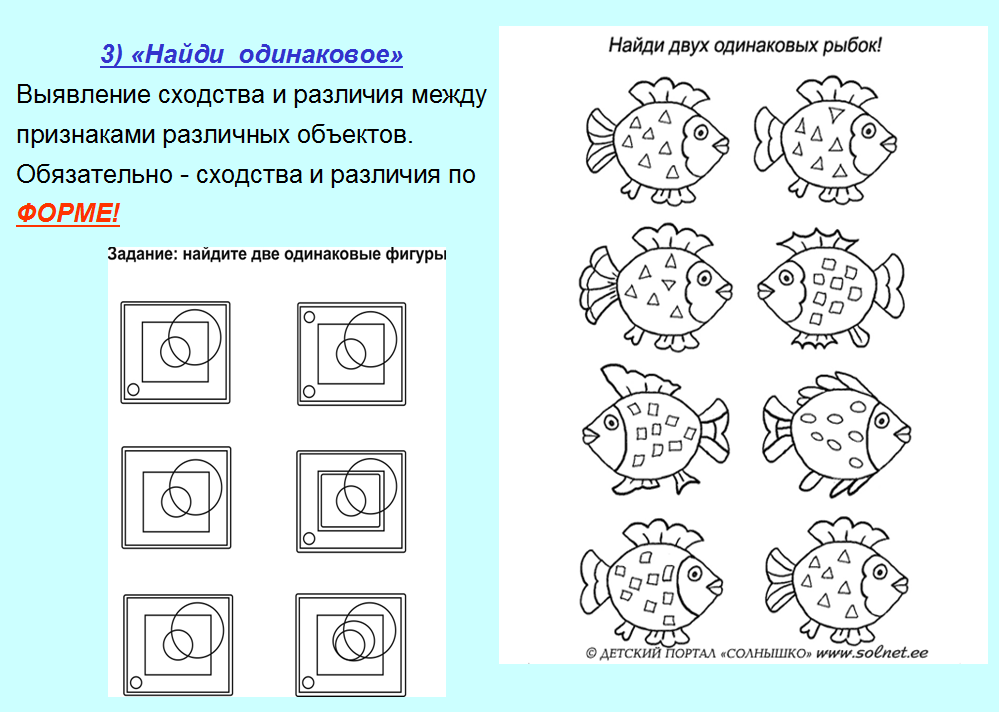
ПРИМЕЧАНИЕ
1. При ответе на вопрос Вы пользуетесь дидактическими материалами из своего Портфолио. Каждая игра – отдельный лист формата А 4.
2. Вы обязательно должны рассказать обо всех 6 вариантах развивающих игр математической направленности в нужной последовательности! Будет проще отвечать, если на обратной стороне Вы подпишете названия игр и пронумеруете их последовательность.
3. Вы не должны при ответе на данный вопрос предлагать игровые упражнения и дидактические игры, чтобы избежать вопросов экзаменационной комиссии по поводу отличия от них развивающих игр математической направленности!
_________________________________________________________________________________
ВОПРОС 9
Определить назначение представленных игровых упражнений для математического развития детей дошкольного возраста. Предложить свои варианты с целью решения подобных задач математического развития.
Приложение: описание игровых упражнений
ОТВЕТ НА ЭКЗАМЕНЕ
Представленные в билете игровые упражнения предназначены для различных этапов развития «чувства времени» у детей старшего дошкольного возраста:
«Чувство времени» — способность мысленно оценивать временные промежутки и ориентироваться во времени.
Формировать у детей «чувство времени» целесообразно в старшем дошкольном возрасте на основе их личного опыта. Детей надо знакомить с такими интервалами времени, которыми можно измерять длительность разнообразных видов их деятельности.
Лучше всего для этих целей использовать временные промежутки – 1 минута, 3 минуты, 5 минут. Можно также познакомить детей и с самым коротким для них промежутком времени – 1 секунда.
- Восприятие времени по песочным часам – учить определять промежутки времени по песочным часам. Я могу предложить свои варианты игровых упражнений (1-2 варианта!)
- Восприятие времени по часам – учить определять промежутки времени по часам. Я могу предложить свои варианты игровых упражнений (1-2 варианта!)
- Оценка промежутка времени без часов для выполнения работы – учить определять объём работы на определённый промежуток времени. Я могу предложить свои варианты игровых упражнений (1-2 варианта!)
- Выполнение работы за определённый промежуток времени без часов - учить оценивать временные интервалы без часов, на основе чувства времени. Я могу предложить свои варианты игровых упражнений (1-2 варианта!)
ПРИМЕЧАНИЕ
Если Вы заранее подготовите и вложите в Портфолио наглядный дидактический материал, Ваш ответ на экзамене будет выглядеть эффектно!
_______________________________________________________________________________
ВОПРОС 10
Предложить варианты игровых упражнений для решения образовательных задач по формированию пространственных представлений на различных возрастных этапах дошкольного детства.
ОТВЕТ НА ЭКЗАМЕНЕ
Пространство – философская категория; это протяженность и объём предметов, расстояние между ними, это - всеобщее свойство материальных тел занимать определенное место и особым образом располагаться среди других материальных тел.
Начиная с раннего возраста, детей учат ориентироваться в пространстве.
Освоение каждой следующей ориентировки в пространстве базируется на прочном знании предыдущей:
1) 2 - 3 года - ориентировка на себе
Я предлагаю такой вариант игрового упражнения…
2) 3 – 4 года - ориентировка на других объектах
Я предлагаю такой вариант игрового упражнения…
3) 3 – 4 года - о риентировка от себя:
- направление от себя
- объект относительно себя
- движение в заданном направлении
Я предлагаю такие варианты игровых упражнений…
4) 4 – 5 лет - ориентировка от других объектов:
- своё положение относительно других объектов
Я предлагаю такой вариант игрового упражнения…
5) 4 - 7 лет - определение взаимного расположения объектов
- объект относительно других объектов
- местоположение объекта относительно другого лица
Я предлагаю такие варианты игровых упражнений…
6) 4 - 7 лет - ориентировка на плоскости листа
Я предлагаю такой вариант игрового упражнения…
ПРИМЕЧАНИЕ
1. При ответе на экзамене необходимо знать и рассказать 6 этапов формирования пространственных представлений у дошкольников, предлагая варианты игровых упражнений для каждого этапа.
2. Отвечать на данный вопрос будет намного легче, если Вы заранее подготовите дидактические материалы в Портфолио – иллюстративный материал к проведению игровых упражнений (ещё проще будет, если Вы подпишете иллюстрации).








_______________________________________________________________________________
Критерии оценки студента на экзамене
| Результат зачета | Критерии |
| «отлично», повышенный уровень | - раскрыты и точно употреблены основные понятия; - сущность вопросов раскрыта полно, развернуто, структурировано, логично; - использованы при ответе примеры, иллюстрирующие теоретические положения; - представлены разные точки зрения на проблему; - выводы обоснованы и последовательны; - диалог с преподавателем выстраивается с обоснованием связи сути вопросов билета с другими вопросами и разделами учебной дисциплины; - полно и оперативно отвечает на дополнительные вопрос; |
| «хорошо», пороговый уровень | - частично раскрыты основные понятия; - в целом материал излагается полно, по сути билета; - использованы при ответе примеры, иллюстрирующие теоретические положения; - выводы обоснованы и последовательны; - выстраивается диалог с преподавателем по содержанию вопроса; - ответил на большую часть дополнительных вопросов; |
| «удовлетворительно», пороговый уровень | - раскрыта только меньшая часть основных понятий; - не достаточно точно употреблял основные категории и понятия; - не достаточно полно и не структурировано отвечал по содержанию вопросов; - не использовал примеры, иллюстрирующие теоретические положения; - не рассматривал разные точки зрения на проблему; - диалог с преподавателем не получился; - возникли проблемы в обосновании выводов, аргументаций; - не ответил на большинство дополнительных вопросов; |
| «неудовлетворительно», уровень не сформирован | - не раскрыто ни одно из основных понятий; - не знает основные определения категорий и понятий дисциплины; - допущены существенные неточности и ошибки при изложении материала; - практическое отсутствие реакции на дополнительные вопросы по билету. |
9. Рекомендуемая литература
Основная литература:
1. 1.Белошистая, А. В. Теория и методика математического развития детей дошкольного возраста: учебник для студ. учреждений сред. проф. образования /А.В. Белошистая. – М. : Издательский центр «Академия», 2017. – 272 с. ил., [16] с. цв. вкл.
2 Белошистая А.В. Формирование и развитие математических способностей дошкольников [Текст]: учебное пособие/ А.В. Белошистая. - М.: ВЛАДОС, 2003.- 400 с.
3. Михайлова З.А., Чеплашкина И.Н. Математика это интересно. Игровые ситуации для детей дошкольного возраста. Диагностика освоения математических представлений, .программа «Детство» - С-П, Детство-пресс 2008.
4. Волина В.В. Праздник числа [Текст]: книга для учителей и родителей/ В.В. Волина. – Москва: Знание, 1993. – 288 с.
5. Новикова, В.П., Тихонова, Л.И. Развивающие игры и занятия с палочками Кюизенера для работы с детьми 3-7 лет - М, Изд-во Мозаика-синтез, 2010 год
6. Данилова В.В. Обучение математике в детском саду [Текст]: практические, семинарские и лабораторные занятия для студентов средних педагогических заведений/ В.В. Данилова. - М.: Просвещение, 1998 - 160 с.
7. Дёмина Е.С. Развитие элементарных математических представлений [Текст]: учебное пособие для студентов, обучающихся по специальности «Дошкольная педагогика и психология», специалистов ДОУ / Е.С. Дёмина. - М.: ТЦ Сфера, 2009. – 128 с.
8. Ерофеева Т.И., Павлова, Л.И. Математика для дошкольников [Текст]: книга для воспитателя детского сада/ Т.И. Ерофеева, Л.И. Павлова. – Москва: Просвещение, 1992. – 191 с.
9. Метлина Л.С. Математика в детском саду [Текст]: учебное пособие/ Л.С. Метлина. - М.: Просвещение, 1984.- 256 с.
10. Медведева, О.С. Психолого-педагогические основы обучения математике. Теория, методика, практика. – М, Изд-во БИНОМ. Лаборатория знаний, 2013.
11. Михайлова З.А., Непомнящая Р.Л. Теоретические и методические вопросы формирования математических представлений у детей дошкольного возраста [Текст]: учебное пособие/ З.А. Михайлова, Р.Л. Непомнящая.- М.: Просвещение, 1988. – 143 с.
12. От рождения до школы. Основная общеобразовательная программа дошкольного образования / Н. Е. Вераксы, Т. С. Комаровой, М. А. Васильевой. - М.: МОЗАИКА-СИНТЕЗ, 2015. - 304 с.
13. Степанова Г.В. Занятия по математике для детей 5-6 лет с трудностями в обучении [Текст]: методическое пособие/ Г.В. Степанова. – М.: ТЦ Сфера, 2010. – 128 с
14.Смоленцева. А.А., Пустовойт О.В. и др. Математике до школы. М., Изд-во: «Детство-Пресс», 2010.
15. Формирование элементарных математических представлений у дошкольников [Текст]: учебное пособие / под ред. А.А.Столяра.- М.: Просвещение, 1988.-303 с.
16. Фрейлах Н.И. Методика математического развития [Текст]: учебное пособие/ Н.И Фрейлах. – М.: Форум, 2006. – 208 с.
17..Федеральный государственный образовательный стандарт дошкольного образования, утвержденный приказом Министерства образования и науки РФ от 17.10.2013г, № 1155
18. Щербакова Е.И. Теория и методика математического развития дошкольников [Текст]: учебное пособие/ Е.И. Щербакова. - М.: Издательство НПО МОДЭК, 2005. – 392 с.19. Хармс,Т. Шкалы для комплексной оценки качества образования в дошкольных образовательных организациях.ECERS-R : переработанное издание / Тельма Хармс, Ричард М. Клиффорд, Дебби Крайер, - М.: Изд-во «Национальное образование», 2016. – 136с.Дополнительная литература:
1. Бондаренко А.К. Дидактические игры в детском саду. [Текст]: учебное пособие / А.К. Бондаренко - М.: Просвещение,1985. - 175 с.
2. Злобенко М.П. Диагностика уровня развития детей дошкольного возраста [Текст]: методическое пособие/ М.П. Злобенко. – Волгоград: Учитель, 2011. - 110 с.
3. Ерофеева Т.И. Дошкольник изучает математику [Текст]: методическое пособие / Т.И. Ерофеева. – М.: Просвещение, 2007. – 80с.
4. Козлова В.А. Обучение дошкольников и младших школьников математике [Текст]: методические рекомендации для родителей и воспитателей/ В.А. Козлова – М.: Школьная пресса, 2002г. – 112с.5. Моргачёва И.Н. Ребёнок в пространстве [Текст]: методическое пособие/ И.Н. Моргачёва. – Санкт-Петербург: ДЕТСТВО-ПРЕСС, 2009. –212 с.
6. Носова Е.А. Логика и математика для дошкольников [Текст]: методическое пособие/ Е.А. Носова - М.: Владос, 2005.- 56 с.
7. Новикова В.П. Математика в детском саду [Текст]: методическое пособие/ В.П. Новикова – М.: ТЦ Сфера, 2000г. – 70с.8. Непомнящая Р.Л. Развитие представлений о времени у детей дошкольного возраста [Текст]: учебно-методическое пособие/ Р.Л. Непомнящая. - СПб.: ДЕТСТВО-ПРЕСС, 2005. –64 с.
9. Попова Г.П. Занимательная математика [Текст]: методическое пособие/ Г.П. Попова. – Волгоград: Учитель, 2006. – 141 с.
10. Бондаренко А.К. Дидактические игры в детском саду. [Текст]: учебное пособие/ А.К. Бондаренко - М.: Просвещение,1985. - 175 с.
Интернет-ресурсы:
1. http://www.academia-moscow.ru/ Издательский центр «Академия»
2. http://www.academia-moscow.ru/ Издательский центр «Академия»
3.http://window.edu.ru/window.
4.http://mimimotik.ru/metodic/matematika/Методика математического развития
5.http://doshkolnik.info/metod/fmat.htm/ Методика математического развития
6.http://www.firo.ru/ Программы дошкольного образования
Дата: 2019-12-09, просмотров: 450.