Чинними інструкціями з побудови Державної геодезичної мережі чітко визначенні вимоги до точності вимірювання кутів і ліній в усіх класах і розрядах мереж. При побудові інженерно – геодезичних мереж полігонометрії часто доводиться через місцеві умови порушувати ці вимоги. Прикладом цього може бути необхідність прив’язки запроектованої мережі до пунктів вищого класу, які знаходяться на значній відстані. При цьому збільшуються довжини сторін прив’язувального ходу. Це знижує точність прив’язки але цього не можна допустити для запроектованої мережі. Щоб цього не сталось, необхідно розрахувати для цих конкретних умов точність кутових і лінійних вимірювань. Впровадження в геодезичне виробництво нових високоточних світловіддалемірів робить вимірювання значно точнішим, ніж цього вимагає інструкція, що дає змогу переглянути точність вимірювання кутів. На будівельних майданчиках може виникнути необхідність створення мережі підвищеної точності при збереженні невеликих довжин сторін тощо. В подібних випадках виникає необхідність розрахунку точності полігонометричних ходів. Вміння розрахувати точність полігонометричних ходів потрібно і кожному майбутньому інженерів, який складатиме інструкції, визначатиме допуски тощо.
Розрахунки точності кутових і лінійних вимірювань базуються на значеннях середніх квадратичних помилок ходів, тощо:
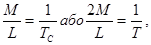(3)
де Тс – знаменник середньої відносної помилки ходу;
Т – знаменник граничної відносної помилки ходу.
Виходячи з принципу однакового впливу помилок кутових і лінійних вимірювання для витягнутого полігонометричного ходу можна записати
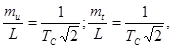(4)
де mu – поперечна середня квадратична помилка положення кінцевої точки ходу;
mt – поздовжня середня квадратична помилка положення кінцевої точки ходу .
Спираючись на цей принцип, перейдемо безпосередньо до розрахунків кутових і лінійних вимірювань.
3.8.1 Розрахунок точності кутових вимірювання.
Для прикладу розрахуємо точність кутових вимірювань у полігонометрії першого розряду. В ході першого розряду 1: Т=1:10000, а n не повинна перевищувати 15. Тоді
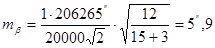(5)
Інструкцією з деяким запасом точності передбачено що mβ = 5”
Уявимо собі, що полігонометричний хід І – розряду запроектовано для розмічувальних робіт. В зв’язку з цим необхідно підвищити його точність до 1:15000. Тоді Тс = 2Т = 30000
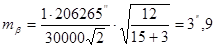(6)
При кутових вимірюваннях основними ждерелами помилок є: центрування теодоліта (mц), редукція (mр), помилки приладу (mп), вплив довкілля (mд), помилки власне вимірювання кутів (mβ), а також помилки вихідних даних (mвих).
Приймаючи, що всі джерела помилок випадкові і дотримуючись принципу однакових впливів, отримаємо:
При mц = mр = mп = mд = mβ= mвих = mβвип (7)
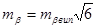(8)
Звідки 
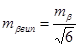(9)
Для полігонометрії І розряду матимемо
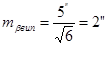
(10)
Граничне значення буде
Δβвип = 2mβвип (11)
Якщо допустити, що всі джерела помилок мають систематичний характер і взяти до уваги принцип різних впливів, то гранична помилка від кожного джерела не повинна перевищувати:
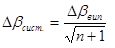
(12)
де n – кількість сторін в ході
Знов таки для полігонометрії І розряду (n = 15) отримаємо:
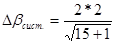(13)
mβ2 = mц2 + mр2 + mп2 + mд2 + mβ2 + m2вих (14)
Виконані розрахунки і виробничий досвід кутових вимірювань показують вимоги до впливу систематичних помилок повинні бути доволі жорсткі. Слід мати також на увазі, що вплив систематичних помилок на поперечний зсув зростає пропорційно до кількості точок у ході, а вплив випадкових помилок зростає приблизно пропорційно кореню квадратному з кількості точок у полігонометричному ході.
Виходячи з попередніх розрахунків, визначимо точність окремих операцій під час вимірювання кутів.
1.Помилка за центрування теодоліта є величиною випадковою, а її вплив на точність вимірювання кутів визначається формулою
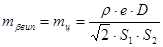(15)
де D – довжина сторони, яка з’єднує візирні цілі на задній і передній точках;
S1, S2 - віддалі від теодоліта до візирних марок;
е- лінійний елемент центрування.
Відповідно для полігонометрії І розряду при Smin =120 м і mц =2”, отримаємо
е =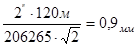 
(16)
2.Помилка за встановлення візирних марок (редукція) також є випадковою,а вплив на точність вимірювання кутів визначається формулою:
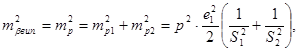(17)
де е1 – лінійний елемент редукції,
Приймаючи S1=S2=S, отримаємо
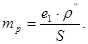(18)
Звідси
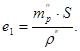(19)
При цих же даних для полігонометрії І розряду е1=1,2 мм, 2 розряду -1,6 мм.
Враховуючи, що теодоліт і марка над точками ходу встановлюються з однаковою точністю, знайдемо сукупний вплив цих двох джерел помилок
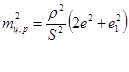(20)
При e = e1 отримаємо
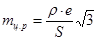(21)
Знов -таки, для полігонометрії І розряду е =1,0 мм, 2 розряду - е ≈1,3 мм.
Щоб досягти такої точності центрування теодоліта і встановлення візирних марок, необхідно користуватись добре вивіреними оптичними висками. Значно зменшити вплив цих помилок можна використовуючи так звану триштативну систему, у якій одні і ті ж штативи по черзі використовуються для встановлення теодоліта і візирних марок. Очевидно, що із збільшенням довжин сторін точність центрування теодоліта і візирних марок можна зменшувати.ак
Незалежно від цього необхідно постійно слідкувати за стійкістю приладів, яка може бути порушена не тільки внаслідок дії вітру, сонця, або внаслідок тремтіння підлоги в цехах, але і механічного руху транспорту, дій посторонніх осіб.
Точність центрування приладів різними видами висків характеризується такими значеннями:
1) звичайний гострокінцевий висок -10 мм (захищений від вітру - 6-8 мм);
2) важкий висок - 5 мм;
3) механічний (штанговий) висок - 2-3 мм;
4) оптичний висок - 0,5-0,7 мм.
3. Помилка самого приладу. Під час вимірювання кутів вважають, що всі геометричні умови в теодоліті виконуються, їх порушення і викликають помилки приладу. Значно послабити ці помилки можна, акуратно виконуючи всі перевірки і дослідження полігонометричного комплекту та ретельного юстування і визначення поправок приладу. Як відомо, деякі помилки приладу виключаються або значно послаблюються відповідною методикою вимірювань. Проте помилка за нахил осі обертання труби, викликана відхиленням основної осі теодоліта від лінії виска, не виключається і методикою вимірювань. Значення цієї помилки розраховується за відомою формулою
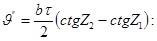(22)
або
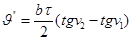; (23)
де b - нахил осі обертання труби;
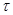- ціна поділки рівня;
Z1, Z2- зенітні відстані напрямків;
V1, v2 - відповідно кути нахилу.
Очевидно, при v1 = v2 маємо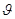 
= 0 , при v1 = v2 значення помилки буде максимальним, тобто
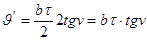(24)
Візьмемо, як і раніше, що
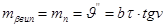(25)
Звідки
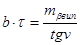(26)
Підставляючи в формулу значення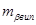 
для відповідного класу (розряду) полігонометрії і задаючись конкретними значеннями кутів нахилу, отримаємо табл. 6
Таблиця 6
| Клас(розряд) полігонометрії | Кут нахилу візирного променя | |||||
| 4 клас 1 розряд 2 розряд | 45° | 300 | 20° | 10° | 5° | 3° |
| 0,6 1,0 2,0 | 1,0 1,7 3,5 | 1,6 2,8 5,5 | 3,4 5,7 11,3 | 6,8 11,4 22,8 | 17,2 28,6 57,3 | |
Аналіз даних цієї таблиці свідчить, що вже при різниці кутів нахилу, більшій за 5°, нахил осі обертання труби не фіксується рівнем (у 2Т2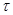 
=15") при відхиленні бульбашки рівня на одну поділку. При використанні інших теодолітів (наприклад, Theo 01ОА , де 
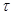=20") проблема ще більше ускладнюється. Все це вимагає від виконавця перед початком і під час робіт старанно приводити основну вісь теодоліта до лінії виска, брата відліки по краях бульбашки рівня і вводити поправки у виміри. В цих випадках доцільно використовувати накладні рівні.
4. Помилка власне вимірювання кута є випадковою. При вимірюванні кутів способом кругових прийомів вона розраховується за формулою
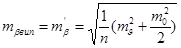(27)
де n - кількість прийомів,
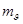- помилка візування,
m0 - помилка відліку.
Помилка візування ( 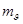) залежить від гостроти зору спостерігача, збільшення
труби, вигляду сітки ниток, форми, розміру і освітлення візирних марок, стану атмосфери тощо. Для попередніх розрахунків можна прийняти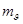 
= 2" (оптичні теодоліти).
В оптичних теодолітах за помилку відліку (m0) переважно вважають помилку суміщання зображень штрихів лімба. Спеціальними дослідженнями встановлено,що при штучному освітленні лімба m0 ≈ 0,”34,а при природному m0 ≈1”. За несприятливих умов m0 ≈ 2", На підставі цих даних можна підрахувати необхідну кількість прийомів,
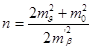(28)
Для полігонометрії 4 класу отримаємо n =5; 1 розряду - 3; 2 розряду - 2, що досить добре узгоджується з вимогами інструкції.
5. Помилка за вплив довкілля при кутових вимірюваннях є явною систематичною помилкою. Довкілля впливає як на положення самого теодоліта, так і на якість візування трубою, Так, під час вимірювання кутів, можливе осідання ніжок штатива, боковий тиск вітру спричиняє зміщення приладу з центру знака, а боковий поривчастий вітер викликає його тремтіння, боковий нагрів штатива веде до різного видовження ближніх і дальніх ніжок штатива, нерівномірна освітленість марок або інших візирних пристосувань призводить до значних помилок візування (помилок фаз). Забрудненість повітря на будівельному майданчику або вулиці погіршує видимість, а це призводить до продовження часу вимірювань а, отже, і їх точності.
Під впливом конвекційних потоків (термічна турбулентність) у приземному шарі повітря виникають коливання зображень візирних пристосувань, що ускладнює візування.
Найбільші викривлення у результати кутових вимірювань вносить бокова рефракція, що виникає внаслідок значних бокових різниць температури біля стін будинків і споруд, башт, труб, працюючого технологічного обладнання. На рис.3.6
показане температурне поле на освітленій сонцем вулиці міста.
З рис. 3.6 випливає, що на віддалі 1,5-2 м від стінки інтенсивності віддачі тепла значно зменшується. Залежність бокової рефракції від метеорологічних елементів визначається формулою
 |
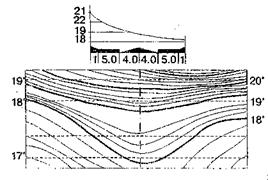Рис.3.6
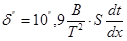(29)
де В - тиск атмосфери, мм;
Т- температура повітря, 0К;
S - довжина лінії візування, м; dT/dx - боковий градієнт температури на 1 м.
Враховуючи, що бокова рефракція явно систематичного характеру, прирівняємо формули
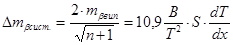(30)
З цієї залежності визначаємо dT/dx.
Приймемо для розрахунків В-750 мм, Т=300°К, 8=500м (4 кл).
Після обчислень отримаємо:
4 клас- dT/dx « 0,01 °/м;
З наведених даних видно, що на міській вулиці із суцільною забудовою знайти періоди дня з такими малими градієнтами температури дуже важко, а отже, потрібні інші методи послаблення впливу бокової рефракції, тобто:
І.Ходи полігонометрії проектувати при можливості вздовж тіньового боку вулиці.
2. Уникати розміщення на шляху візирного променя об'єктів з сильним тепловим випромінюванням.
3. Віддаляти сторони полігонометричного ходу від освітлених сонцем будинків не менше як на 1,5-2 м.
4. Кутові вимірювання виконувати у ранкові та вечірні години спокійних зображень, коли значно вирівнюється температура як по вертикалі, так і по горизонталі. Максимально використовувати дні з похмурою погодою, весняні та осінні періоди. Полудень повинен бути виключеним зі спостережень кутів.
5. При встановленні штативів з-під ніжок необхідно прибрати дерн, а на асфальті в літні сонячні дні робити невеликі заглиблення. Ніжки штатива і теодоліт необхідно захищати від прямих сонячних променів.
6. Постійно слідкувати за станом центрування теодоліта і візирних марок.
7.Припиняти кутові вимірювання, якщо вітер викликає тремтіння приладу.
8. На слабших ґрунтах під ніжки штатива необхідно забивати кілки.
9. Помилки вихідних даних не впливають на точність кутових вимірювань, але впливають на кутову нев'язку в ході. З метою їх послаблення необхідна якнайчастіша прив'язка ходу до пунктів вищого класу або застосування гіроскопічного орієнтування.
Дата: 2019-12-22, просмотров: 363.
