Разработка модели обучения школьному курсу стереометрии на модульной основе

Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Разработка модели обучения школьному курсу стереометрии на модульной основе

Выпускная квалификационная работа

по специальности 050201 «Математика»

СОДЕРЖАНИЕ

ВВЕДЕНИЕ

Глава 1. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ МОДУЛЬНОЙ СИСТЕМЫ ОБУЧЕНИЯ

1.1 АНАЛИЗ ЛИТЕРАТУРЫ ПО ПРОБЛЕМЕ ИССЛЕДОВАНИЯ

1.2 СУЩНОСТЬ МОДУЛЬНОГО ОБУЧЕНИЯ

1.3 ПРИНЦИПЫ МОДУЛЬНОГО ОБУЧЕНИЯ И УСЛОВИЯ ИХ РЕАЛИЗАЦИИ

1.4 ОРГАНИЗАЦИЯ УЧЕБНО-ВОСПИТАТЕЛЬНОГО ПРОЦЕССА ОБУЧЕНИЯ СТЕРЕОМЕТРИИ

1.5 МОДУЛЬНОЕ СТРУКТУРИРОВАНИЕ И ОРГАНИЗАЦИЯ УЧЕБНЫХ ЗАНЯТИЙ ПО СТЕРЕОМЕТРИИ

ВЫВОДЫ ПО ПЕРВОЙ ГЛАВЕ

Глава 2. РАЗРАБОТКА МОДУЛЬНОЙ СТРУКТУРЫ ПРОЦЕССА ОБУЧЕНИЯ СТЕРЕОМЕТРИИ В СИСТЕМЕ ШКОЛЬНОГО ОБРАЗОВАНИЯ

2.1 МОДЕЛЬ ОБУЧЕНИЯ ШКОЛЬНОМУ КУРСУ СТЕРЕОМЕТРИИ НА МОДУЛЬНОЙ ОСНОВЕ

2.2 ОРГАНИЗАЦИЯ ВНЕДРЕНИЯ РАЗРАБОТАННОЙ МОДЕЛИ

2.3 АНАЛИЗ ВНЕДРЕНИЯ МОДЕЛИ

2.4 СОПОСТАВЛЕНИЕ РЕЗУЛЬТАТОВ КОНСТАТИРУЮЩЕГО И КОНТРОЛЬНОГО СРЕЗОВ

ВЫВОДЫ ПО ВТОРОЙ ГЛАВЕ

ЗАКЛЮЧЕНИЕ

СПИСОК ЛИТЕРАТУРЫ

Приложение 1

Приложение 2

Приложение 3

Приложение 4

Приложение 5

ВВЕДЕНИЕ

В соответствии с современными тенденциями развития общества для системы образования все более характерными становятся такие принципиальные новые черты, как динамизм и вариативность.

Традиционная система организации учебно-воспитательного процесса находится в противоречии с законами и закономерностями психофизиологической деятельности человека и теории управления. Классно-урочная система характеризуется многопредметностью и низкой частотностью учебных предметов, что предопределяет постоянную перегрузку ученика и учителя. Ведущим типом учебного занятия остается комбинированный урок, нарушающий логику учебной деятельности и особенно нежелательный в старших классах школы.

Отечественная и зарубежная практика показывает перспективность принципиально иного по организации и технологии модульного обучения, которое характеризуется опережающим изучением теоретического материала укрупненными блоками-модулями, алгоритмизацией учебной деятельности, завершенностью и согласованностью циклов познания и других циклов деятельности. Поуровневая индивидуализация учебной и дифференциация обучающей деятельности создают ситуацию выбора для учителя и ученика и обеспечивают школьнику возможность дальнейшего успешного самообразования и профессионального образования [49].

Если рассматривать модульную систему организации учебно-воспитательного процесса утилитарно, то обучающая технология будет сведена к следующему: законченность блоков содержания, интеграция видов и форм обучения, каждый учащийся достигает поставленных целей и может самостоятельно работать с предложенной ему индивидуальной учебной программой. Гибкость такой технологии объясняется адаптацией к индивидуальным особенностям обучаемых за счет исходной диагностики знаний, темпа усвоения и индивидуализации обучения.

В подавляющем большинстве случаев использование технологии модульного обучения осуществляется на эмпирической основе, без должной проработки ее научно-методической стороны, исходя только из опыта и здравого смысла преподавателя. Для перехода педагогической системы обучения стереометрии в новое качество необходима дальнейшая разработка теоретико-методологических оснований модульного обучения и вытекающих из них научных средств познания, форм и методов обучения, соответствующих модульной системе [8].

Таким образом, актуальность темы исследования определяется состоянием практики обучения геометрии в системе школьного образования. Она обусловлена необходимостью обоснованного подхода к разработке средств на базе модульных технологий с диагностированием уровней сформированности знаний, умений учащихся на различных этапах формирования геометрических понятий.

Проблема исследования: каковы теоретико-методологические основы процесса обучения стереометрии школьников 10-11-х классов на модульной основе, влияющие на повышение качественного уровня геометрической подготовки учащихся.

Объектом исследования является процесс обучения геометрии в школе на модульной основе.

Предмет исследования: основные организационные и содержательные компоненты модели обучения школьному курсу стереометрии на модульной основе.

Цель исследования: теоретически обосновать и разработать модель обучения школьному курсу стереометрии на модульной основе.

В соответствии с поставленной целью была сформулирована следующая гипотеза исследования: овладение школьным курсом стереометрии будет наиболее эффективным при условии внедрения в процесс обучения разработанной нами модели с использованием модульной технологии, позволяющей осуществлять целенаправленное управление формированием и совершенствованием практических навыков учащихся, адаптировать процесс обучения к индивидуально-психологическим особенностям, способствуя тем самым развитию активного и творческого подхода к изучению стереометрии.

Задачи исследования:

1. Изучить состояние проблемы использования модульного обучения в психолого-педагогической теории и практике.

2. Выявить в ходе научно-педагогического анализа основные направления и степень разработанности приемов модульного обучения в средней школе.

3. Раскрыть сущность и принципы модульной технологии, условия ее реализации в процессе обучения стереометрии.

4. Определить перспективные направления совершенствования процесса овладения курсом стереометрии, способствующие повышению эффективности геометрической подготовки школьников.

5. Разработать и теоретически обосновать модель обучения школьному курсу стереометрии на модульной основе.

6. Определить педагогическую эффективность использования модульной технологии в преподавании стереометрии.

7. Экспериментально проверить эффективность и результативность разработанной модели обучения школьному курсу стереометрии на модульной основе.

Теоретико-методологическую базу исследования составляют:

1. Философские, психолого-педагогические концепции познания как общественно-исторического процесса (Шамовой Т.И., Гараева В.М., Громковой М.Т., Гальпериным П.Я.)

2. Использование системного подхода в разработке модульного обучения (Андреева М.В., Лебедевой М.Б., Третьякова П.И., Чернилова Н.Г.).

3. Методология педагогических исследований, в которых рассмотрены закономерности соотношения обучения и развития интеллекта (Апатова Н.В.).

4. Теоретической базой исследования послужили работы, посвященные тенденциям развития информатики в современной общеобразовательной средней школе: Н.В. Апатовой, Т.Н. Брусенцовой, Я.А. Ваграменко, Ю.А. Гольцмана, Т.Ю. Ильиной, Т.Б. Казиахмедова, М.П. Лапчика, Н.И. Пака, Ю.А. Первина, И.В. Роберт, И.А. Румянцева, И.В. Симоновой, Е.И. Соколовой.

Для решения поставленных задач использовались следующие методы исследования: анализ педагогической и методической литературы; теоретические методы для разработки модели обучения школьному курсу стереометрии на модульной основе; эмпирические методы для внедрения разработанной модели обучения стереометрии на модульной основе в процесс овладения предметом; математические методы для обработки данных, полученных в ходе внедрения разработанной методики.

Практическая значимость работы заключается в разработке модели обучения школьному курсу стереометрии на модульной основе и разработке обучающих модулей по темам: «Параллельность прямых и плоскостей в пространстве», «Перпендикулярность прямых и плоскостей в пространстве».

Теоретическая значимость исследования состоит в следующем:

1. Проведен анализ педагогической, психологической и методической литературы по проблеме исследования, обобщены и систематизированы научные положения в данной области.

2. Выделены принципы модульного обучения стереометрии.

3. Разработана методика обучения стереометрии с использованием модели овладения курсом.

Первая глава посвящена теоретическому обоснованию модульной системы обучения. Проанализирована литература по проблеме исследования. Рассмотрены сущность и принципы модульного обучения. А также разработана модель обучения школьному курсу стереометрии.

Во второй главе представлены результаты внедрения разработанной нами модели в процесс обучения стереометрии, анализ проведенных уроков.

ВЫВОДЫ ПО ПЕРВОЙ ГЛАВЕ

1. Модульное обучение зародилось в конце 60-х годов. В его основу положено понятие «модуль». Модуль – это логически завершенная часть учебного материала. Модульное обучение отличается от других систем обучения тем, что содержание представляется в законченных самостоятельных блоках, меняется форма общения ученика и учителя, ученик работает максимум времени самостоятельно, а также тем, что наличие модулей позволяет учителю индивидуализировать работу с отдельными учениками.

2. Внедряемые в практику новые педагогические технологии обучения, модульной организации учебного процесса позволяют модернизировать традиционные методы обучения. Положительная роль модульного обучения связана с осознанностью перспективы обучения каждым учеником.

3. Сущность модульного обучения заключается в том, что обучающийся более самостоятельно может работать с предложенной ему индивидуальной программой, включающей в себя целевой план действий, банк информации и методическое руководство по достижению поставленных дидактических целей.

4. Выделяют следующие принципы модульного обучения: принцип модульности, принцип структурирования содержания обучения, принцип гибкости, принцип оперативности, принцип паритетности, принцип динамичности, принцип деятельного подхода, принцип осознанной перспективы и принцип разностороннего методического консультирования.

5. Программа учебной дисциплины состоит из системы модулей. В программу учебного модуля отбираются учебные элементы, которые, будучи представлены в целом и взаимосвязи, образуют логическую структуру.

6. Модуль имеет следующую структуру: открытие модуля (обычно в виде лекции), серия уроков-семинаров, серия уроков-практикумов, контроль в форме зачета или контрольной работы и обобщение модуля. Относительно уровня сложности и трудности изучаемой темы всех учащихся внутри класса или параллели целесообразно разделить на три группы.

7. Освоение модульной системы предусматривает формирование содержания стереометрии из учебных модулей, состоящих из блоков-модулей содержания теоретического учебного материала и блоков алгоритмических предписаний учебных умений и навыков.

8. Главное достоинство модульной системы заключается в возможности плавного перехода от существующей организации учебно-воспитательного процесса, без ее разрушений и нежелательных деформаций в ней, к новым моделям педагогической технологии.

Глава 2. РАЗРАБОТКА МОДУЛЬНОЙ СТРУКТУРЫ ПРОЦЕССА ОБУЧЕНИЯ СТЕРЕОМЕТРИИ В СИСТЕМЕ ШКОЛЬНОГО ОБРАЗОВАНИЯ

АНАЛИЗ ВНЕДРЕНИЯ МОДЕЛИ

Апробирование методики с использованием разработанной нами модели на основе модульной технологии мы проводили на примере тем: «Параллельность прямых и плоскостей в пространстве», «Перпендикулярность прямых и плоскостей в пространстве» (Приложение 4).

В проведенных уроках использовались следующие формы организации работы учащихся:

- коллективная работа учащихся всего класса;

- работа учащихся в парах.

В процессе работы в парах учащимся предлагался разработанный модуль, изучая который в течение определенного времени, они ознакамливались с теоретическим материалом, искали ответы на поставленные перед ними вопросы. В ходе коллективной работы весь класс отвечал на поставленные вопросы, решал предоставленные им задания.

Процесс обучения происходил с помощью модулей, учебными элементами которых являлись: цель, ознакомление с теоретическими положениями, исторические сведения, проверка усвоения теоретического материала, участие в учебной беседе, самостоятельное выполнение заданий, выполните контрольных заданий. Каждый школьник обучался в индивидуальном темпе по своей программе. Учитель выступал в роли консультанта.

Перечислим методы, используемые в рамках разработанной нами модели (по Ю.К. Бабанскому).

Методы обучения
Основная подгруппа	Отдельные методы обучения
1. Методы стимулирования и мотивации учения
1.1. Методы формирования интереса к учению	1.1. Познавательные игры, учебные дискуссии, методы эмоционального стимулирования
1.2. Методы формирования чувства долга и ответственности в учении	1.2. методы учебного поощрения, порицания, предъявления учебных требований
2. Методы организации и осуществления учебных действий и операций
2.1. Перцептивные методы (передачи и восприятия учебной информации посредством чувств): словесные наглядные аудиовизуальные практические	Лекция, рассказ, беседа Иллюстрация, демонстрация Сочетание словесных и наглядных Упражнения
2.2. Логические методы (организация и осуществление логических операций)	Индуктивные, дедуктивные, аналогии и пр.
2.3. Гностические методы (организация и осуществление логических операций)	Проблемно-поисковые (проблемное изложение, эвристический, исследовательский), репродуктивные (инструктаж, иллюстрирование, объяснение и практическая тренировка)
2.4. методы самоуправления учебными действиями	Самостоятельная работа
3. Методы контроля и самоконтроля
3.1. методы контроля	Устный, письменный, лабораторный и машинный контроль, самоконтроль

Дадим описание и анализ каждого из проведенных модулей.

Первый модуль посвящен теме «Параллельность прямых и плоскостей в пространстве». Обучаясь по нему учащиеся познакомились с:

- определениями параллельных и скрещивающихся прямых в пространстве, прямой, параллельной плоскости, параллельных плоскостей в пространстве;

- случаями взаимного расположения прямых, прямой и плоскости, а также двух плоскостей в пространстве;

- основными теоремами данной темы;

- способами задания плоскости в пространстве,

- историческими сведениями по теме изучения.

А также закрепили полученные знания на практике путем обсуждения теоретических вопросов в устной беседе, решением заданий, как элементарных, так и повышенного типа.

Рис.4

После изучения первого модуля с учащимися проведен промежуточный срез.

1. Каково взаимное расположение прямых KE и MH, если точки K, E, M, H – середины ребер AB, BC, CD, DA тетраэдра ABCD (рис.4)?

(А) пересекаются	(В) скрещиваются
(Б) параллельны	(Г) могут быть пересекающимися, параллельными и скрещивающимися (в зависимости от вида тетраэдра)

2. Каково взаимное расположение прямых KM и BC? (Рис.4)

(А) пересекаются	(В) скрещиваются
(Б) параллельны	(Г) возможны все три случая (А) – (В)

3. Каково взаимное расположение прямых AB₁ и BD₁, если дан прямоугольный параллелепипед ABCDA₁B₁C₁D₁? (Рис.5)

(А) скрещиваются	(В) параллельны	(Д) не определить
(Б) пересекаются	(Г) пересекаются или параллельны

B C

A D

A D

Рисунок 5

4. Какие из прямых b = BB₁, c = CC₁, d = D₁C₁ скрещиваются с прямой a = AB? (Рис.5)

(А) только b	(В) только c и d	(Д) все три прямые b, c, d
(Б) только c	(Г) только b и c

5. Каково взаимное расположение прямой B₁C₁ и плоскости BDA₁? (Рис.5)

(А) параллельны	(В) пересекаются или параллельны
(Б) пересекаются	(Г) ответ отличен от (А) – (В)

6. Каково взаимное расположение плоскостей BDA₁ и B₁D₁C? (Рис.5)

(А) параллельны	(В) пересекаются или параллельны
(Б) пересекаются	(Г) ответ отличен от (А) – (В)

7. В пространстве даны прямая a и точка M. Сколько существует прямых, проходящих через M и параллельных прямой a?

(А) 0	(В) бесконечно много	(Д) 1 или бесконечно много
(Б) 1	(Г) 0 или 1

8. Даны параллельные прямая a и плоскость α. Сколько существует плоскостей, проходящих через a и параллельных α?

(А) 0	(В) бесконечно много	(Д) бесконечно много
(Б) 1	(Г) 0 или 1

9. В пространстве даны две параллельные прямые a и b. Сколько существует плоскостей, проходящих через прямую a и параллельных прямой b?

(А) 0	(В) бесконечно много	(Д) 1 или бесконечно много
(Б) 1	(Г) 0 или 1

10. Даны две пересекающиеся плоскости α, β и не лежащая на них точка M. Сколько существует прямых, проходящих через M и параллельных плоскостям α и β?

(А) 0	(В) бесконечно много	(Д) 0 или бесконечно много
(Б) 1	(Г) 0 или 1

11. Даны две скрещивающиеся прямые a и b. Сколько существует пар параллельных плоскостей, одна из которых проходит через a, а другая – через b?

(А) 0	(В) бесконечно много	(Д) 0 или бесконечно много
(Б) 1	(Г) 0 или 1

12. В пространстве даны две пересекающиеся прямые a, b и не лежащая на них точка M. Сколько существует плоскостей, проходящих через M и параллельных прямым a и b?

(А) 0	(В) бесконечно много	(Д) 0 или бесконечно много
(Б) 1	(Г) 0 или 1

13. Точки A, B и середина M отрезка AB проектируются в точки A₁, B₁ и M₁. Чему равна длина отрезка MM₁, если AA₁ = 3 см, B₁B = 7 см?

(А) 5 см	(В) 2 см	(Д) ответ отличен от указанных
(Б) 4 см	(Г) 5 см или 2 см

14. Если два луча, не лежащие на одной прямой, параллельны и лежат в одной полуплоскости относительно некоторой прямой, то они называются …

15. На кубе (рис. 6) укажите прямые, проходящие через т.В и скрещивающиеся с прямой ДС₁.

16. На кубе (рис. 6) укажите ребра, параллельные ребру АВ.

17. Угол между прямыми ДС₁ и Д₁С равен 90° (рис. 7). Определите, чему равен угол между А₁В и ДС₁?

18. Угол между прямыми ДЕ и EF равен 60° (рис. 7). Чему равен угол между прямыми ДВ и ВС?

19. Прямые а и в – скрещивающиеся. Известно, что прямая а лежит в плоскости α. Определите, может ли прямая в лежать в плоскости α. объясните почему.

20. Прямые а и в пересекаются. Прямая с является скрещивающейся с прямой а. Могут ли прямые в и с быть параллельными?

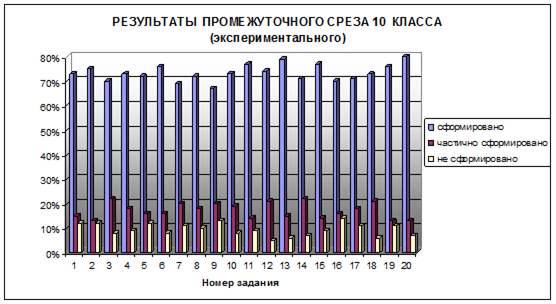
Результаты в экспериментальном классе оказались следующие:

- с первым заданием справились полностью 73%, 15% справились частично, 12% не справились;

- со вторым заданием 75% справились полностью, 13% справились частично, 12% не справились;

- с третьим заданием справились полностью 70%, 22% справились частично, 8% не справились;

- с четвертым заданием 73% справились полностью, 18% справились частично, 9% не справились;

- с пятым заданием 72% справились полностью, 16% справились частично, 12% не справились.

- с шестым заданием 76% справились полностью, 16% справились частично, 8% не справились.

- с седьмым заданием 69% справились полностью, 20% справились частично, 11% не справились.

- с восьмым заданием 72% справились полностью, 18% справились частично, 10% не справились.

- с девятым заданием справились полностью 67%, 20% справились частично, 13% не справились;

- с десятым заданием справились полностью 73%, 19% справились частично, 8% не справились;

- с одиннадцатым заданием справились полностью 77%, 14% справились частично, 9% не справились;

- с двенадцатым заданием справились полностью 74%, 21% справились частично, 5% не справились;

- с тринадцатым заданием справились полностью 79%, 15% справились частично, 6% не справились;

- с четырнадцатым заданием справились полностью 71%, 22% справились частично, 7% не справились;

- с пятнадцатым заданием справились полностью 77%, 14% справились частично, 9% не справились;

- с шестнадцатым заданием справились полностью 70%, 16% справились частично, 14% не справились;

- с семнадцатым заданием справились полностью 71%, 18% справились частично, 11% не справились;

- с восемнадцатым заданием справились полностью 73%, 21% справились частично, 6% не справились;

- с девятнадцатым заданием справились полностью 76%, 13% справились частично, 11% не справились;

- с двадцатым заданием справились полностью 80%, 13% справились частично, 7% не справились.

В контрольном классе при проведении аналогичного промежуточного среза результаты получились следующие:

- с первым заданием справились полностью 70%, 12% справились частично, 18% не справились;

- со вторым заданием 70% справились полностью, 11% справились частично, 19% не справились;

- с третьим заданием справились полностью 62%, 25% справились частично, 13% не справились;

- с четвертым заданием 53% справились полностью, 23% справились частично, 24% не справились;

- с пятым заданием 59% справились полностью, 15% справились частично, 26% не справились

- с шестым заданием 62% справились полностью, 19% справились частично, 19% не справились;

- с седьмым заданием 68% справились полностью, 18% справились частично, 14% не справились.

- с восьмым заданием 69% справились полностью, 20% справились частично, 11% не справились.

- с девятым заданием справились полностью 62%, 21% справились частично, 17% не справились;

- с десятым заданием справились полностью 76%, 14% справились частично, 10% не справились;

- с одиннадцатым заданием справились полностью 72%, 12% справились частично, 16% не справились;

- с двенадцатым заданием справились полностью 70%, 20% справились частично, 10% не справились;

- с тринадцатым заданием справились полностью 81%, 10% справились частично, 9% не справились;

- с четырнадцатым заданием справились полностью 75%, 24% справились частично, 11% не справились;

- с пятнадцатым заданием справились полностью 73%, 12% справились частично, 15% не справились;

- с шестнадцатым заданием справились полностью 65%, 21% справились частично, 14% не справились;

- с семнадцатым заданием справились полностью 68%, 15% справились частично, 17% не справились;

- с восемнадцатым заданием справились полностью 70%, 16% справились частично, 14% не справились;

- с девятнадцатым заданием справились полностью 75%, 15% справились частично, 10% не справились;

- с двадцатым заданием справились полностью 76%, 14% справились частично, 10% не справились.

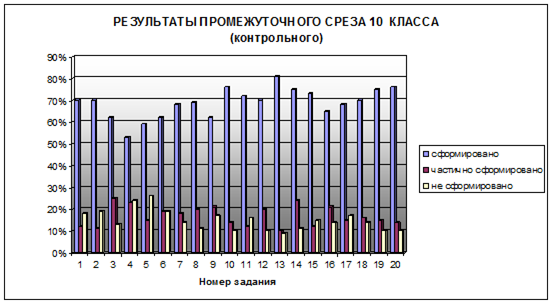
Сравнивая полученные результаты видно, что в экспериментальном классе результаты улучшились благодаря тому, что обучение происходило на основе разработанной модели с использованием модульной технологии.

Структура второго модуля аналогична первому. Он разработан на тему «Перпендикулярность прямых и плоскостей в пространстве». Целью овладения данным модулем является: усвоить понятие угла в пространстве, угла между двумя пересекающимися прямыми в пространстве, перпендикулярных прямых в пространстве, перпендикулярных скрещивающихся прямых, рассмотрение случаев нахождения угла между скрещивающимися прямыми; усвоить понятие прямой, перпендикулярной плоскости, перпендикуляра, высоты пирамиды, прямого цилиндра, рассмотреть признак перпендикулярности прямой и плоскости; усвоить понятие наклонной к плоскости, угла между наклонной и плоскостью, между отрезком и плоскостью; рассмотреть теоремы о трёх перпендикулярах, о перпендикуляре, проведённом из точки к плоскости, об угле между наклонной и плоскостью, научится применять полученные знания при доказательстве определенных фактов и при решении задач практического характера. Обучаясь с помощью данного модуля учащиеся познакомились с:

- определением угла в пространстве, угла между скрещивающимися прямыми, угла между наклонной и плоскостью, угла между соответствующей прямой и плоскостью;

- определением прямой, перпендикулярной плоскости, наклонной к плоскости;

- расстоянием между плоскостью и точкой, между параллельными прямыми;

- понятием общего перпендикуляра;

- основными теоремами данной темы;

Закрепили полученные знания в ходе устной беседы, решая задания на первичное закрепление и в измененной ситуации.

В процессе изучения тем «Параллельность прямых и плоскостей в пространстве» и «Перпендикулярность прямых и плоскостей в пространстве» нам удалось охватить весь объем теоретической информации. Нами были рассмотрены и отработаны задания на отработку основных умений и навыков, которые были сформированы в процессе обучения по данным модулям. При решении упражнений возникшие затруднения сразу устранялись по мере их возникновения и решались подобные задания на закрепление пройденного материала. Они были достаточно интересны, разнообразны и разноуровневы по своему содержанию, отличались новизной формулировок, а также тем, что необходимо было логически мыслить при поиске ответа на поставленный вопрос. Занятия дали положительный результат по формированию следующих умений:

- анализировать наблюдаемые предметы и явления, выделять в них существенное, главное, отбрасывать второстепенное и находить общее;

- выявлять причинно-следственные связи и отношения объектов, систематизировать факты на новом уровне;

- концентрировать общие положения, отыскивать доказательства, путем абстрагирования и обобщения раскрывать сущность новых понятий;

- видеть проблему и находить несколько способов ее решения с целью выявления наиболее рационального и оригинального;

- осуществлять перенос усвоенных знаний и способов деятельности в новые условия и для дальнейшего самообразования;

Для сравнения результатов констатирующего среза по улучшению работы был проведен контрольный срез. Ему посвящен следующий параграф.

ВЫВОДЫ ПО ВТОРОЙ ГЛАВЕ

1. На основе анализа психолого-педагогической и методической литературы, опыта преподавания стереометрии в школе разработана модель обучения школьному курсу стереометрии на модульной основе.

2. Разработаны и проверены на занятиях задания, позволяющие судить об уровне сформированности выделенных умений до и после апробации.

3. Разработаны модули по темам «Параллельность прямых и плоскостей в пространстве», «Перпендикулярность прямых и плоскостей в пространстве» и проведены уроки с их использованием.

4. Процесс обучения происходил с помощью разработанных модулей, учебными элементами которых являлись: цель, ознакомление с теоретическими положениями, исторические сведения, проверка усвоения теоретического материала, участие в учебной беседе, самостоятельное выполнение заданий, выполните контрольных заданий. Каждый школьник обучался в индивидуальном темпе по своей программе. Учитель выступал в роли консультанта.

5. На основании проведенной работы можно сделать вывод, что занятия, организованные предложенным способом, являются эффективными.

ЗАКЛЮЧЕНИЕ

Проблемы по применению технологии модульной системы обучения очень актуальна. Внедрение этой технологии позволяет создать такую систему обучения, которая обеспечивает образовательные потребности каждого ученика в соответствии с его склонностями, интересами и возможностями, а также создаёт необходимость внесения существенных изменений в организацию учебного процесса. При этом учитываются требования дифференцированного подхода, гарантируется возможность усвоения программного материала на базовом уровне всеми учащимися и на продвинутом (повышенном) уровне темы, которые определили для себя данный уровень обучения.

Таким образом, технология модульного обучения обеспечивает:

- законченность блоков содержания: целевой план действий, банк информации и методическое руководство по достижению поставленных дидактических целей;

- интеграцию методов и форм обучения;

- снижение нагрузки на обучаемых и преподавателей

- повышение качества знаний;

- снятие излишней стрессовой нагрузки;

- достижение каждым учеником поставленных целей;

- самостоятельности школьника при работе по индивидуальной учебной программе;

- варьирование функций учителя (от информационно - контролирующей до консультативно - координирующей).

Технология модульного обучения обладает следующими свойствами:

- динамичностью, что проявляется в вариативности содержания, возможности обучения различным способам деятельности;

- гибкостью, которая предполагает адаптивность к индивидуальным особенностям обучаемых за счёт исходной диагностики знаний, темпа усвоения и индивидуализации обучения;

- перспективностью, которая обеспечивается знакомством учащегося со всей модульной программой, с комплексной дидактической целью (с учётом близких, средних и далёких задач);

- паритетностью, предполагающей относительно самостоятельный характер учебного труда школьников и возможность совместного выбора оптимального пути обучения.

Результаты практического применения данной технологии показывает, что эффективность модульного обучения зависит от ряда условий:

- качества модульной программы и модулей;

- грамотной организации обучения;

- удачного подбора методов обучения;

- педагогическая мастерская преподавателя;

На основании педагогических теорий, достижений в геометрической науке нами определены перспективные направления совершенствования преподавания данного предмета, способствующие повышению эффективности геометрической подготовки школьников. Ими являются: определение дидактических условий, системы средств повышения уровня геометрических знаний, самостоятельности и активности в их приобретении.

Опираясь на методологию модульного подхода, нами сделан вывод о том, что в основу совершенствования геометрической подготовки школьников должна быть положена концепция модульного обучения школьного курса стереометрии. Сформулированы и обоснованы пять ее принципов: принцип модульности, принцип структурирования содержания обучения, принцип гибкости, принцип оперативности, принцип паритетности.

Опираясь на основные положения концепции, нами рассмотрены сущность модульно обучения, организация учебно-воспитательного процесса обучения стереометрии, а также модульное структурирование и организация учебных занятий по стереометрии. Особое внимание нами уделено методу учебных проектов и основной форме обучения – уроку. Проанализировав учебную деятельность, мы пришли к выводу, что как школьники, так и многие учителя не полностью осознают возможности модульной технологии. Причиной этого является то обстоятельство, что применение указанной выше технологии в процессе обучения стереометрии еще недостаточно изучено, поэтому данное исследование является необходимым и современным. Приведем его основные результаты.

1. Установлено, что, традиционная методика обучения геометрии в школе не всегда обеспечивает формирование глубоких фундаментальных знаний по предмету и умение применять их на практике.

2. Теоретически обоснована и разработана методическая система геометрической подготовки школьников, в том числе: выбран концептуальный подход к определению понятия модуля, указаны и обоснованы основные подходы к модульному обучению; сформулированы критерии отбора геометрического содержания в модули и определены основные этапы их построения.

Также нами разработана модель обучения стереометрии на модульной основе, составлены модули на темы: «Параллельность прямых и плоскостей в пространстве», «Перпендикулярность прямых и плоскостей в пространстве», проведено их апробирование.

В результате проведенного исследования была достигнута его цель, подтверждена выдвинутая гипотеза и получены позитивные результаты в решении всех поставленных задач.

СПИСОК ЛИТЕРАТУРЫ

1. Бабанский, Ю.К. Проблемы повышения эффективности педагогических исследований [Текст] / Ю.К. Бабанский– М., 1982. – 256 с.

2. Батышев, С.Я. Блочно-модульное обучение [Текст] / С.Я. Батышев – М., Транс-сервис, 1997. – 225 с.

3. Беспалько, В.П. Слагаемые педагогической технологии [Текст] / В.П. Беспалько – М.: Педагогика, 1989. – 523 с.

4. Блохин, Н. В. Психологические основы модульного профессионально ориентированного обучения: Методическое пособие [Текст] / Н.В. Блохин, И.В. Травин. – Кострома: Изд-во КГУ им. Н.А. Некрасова, 2003. – 14 с.

5. Борисова, Н.В. Использование модульной системы обучения в профессиональной подготовке кадров [Текст] / Н.В. Борисова, Н.А. Гудков, В.П. Бугрин, В.Б. Кузов // “Персонал”. – 2000 г. – № 1. – с. 24-30.

6. Вазина, К.Я. Саморазвитие человека и модульное обучение [Текст] / К.Я. Вазина. – Н. Новгород, 1991. – 163 с.

7. Варенова, Л.И. Рейтиноговая Интенсивная Технология Модульного обучения [Текст] / Л.И. Варенова, В.Ж. Куклин, В.Г. Наводнов. – М.: Педагогика, 1993. – 67 с.

8. Васильева, И.Н. Интегративное обучение и модульные педагогические технологии [Текст] / И.Н. Васильева, О. А. Чепенко // Специалист. – 1997 г. – № 6. – с.13-15.

9. Вульфсон, Б.Л. Модернизация содержания гуманитарного образования в школах Запада [Текст] / Б.Л. Вульфсон // Советская педагогика. – 1991 г. №1. – с.124-130.

10. Галочкин, А.И. Основы проблемно-модульной технологии обучения [Текст] / А.И. Галочкин, Н.Г. Базарнова, В.И. Маркин и др. – Барнаул: Изд-во Алт. ун-та, 1998. – 101 с.

11. Гальперин, П.Я. Методы обучения и умственное развитие ребенка. [Текст] / П.Я. Гальперин. – М.: Просвещение, 1985. – 79 с.

12. Гараев, В.М. Принципы модульного обучения [Текст] / В.М. Гараев, С.И. Куликов, Е.М. Дурко // Вестник высшей школы. – 1997. – №8. – с. 30-33.

13. Голощёкина, Л.П. Модульная технология обучения. Методические рекомендации [Текст] / Л.П. Голощёкина, В.С. Збаровски. – С. Петербург: Дрофа, 1993. – 67 с.

14. Громкова, М.Т. Модульное обучение в системном образовании взрослых [Текст] / М.Т.Громкова. – Москва: Просвещение, 2000. – 79 с.

15. Денисов, И.Н. Модульный принцип – основа современного образования [Текст] / И.Н. Денисов, Р.Г. Артамонов, Э.Г Улумбеков, Г.Э. Улумбекова. – Москва: Просвещение, 2005. – 29 с.

16. Дикунов, А.М. Перспективы модульной технологии педагогического контроля [Текст] / А.М. Дикунов // Теория и практика физической культуры. – 1997. - №12. – С. 21-26.

17. Глейзер, Г.Д. Индивидуализация и дифференциация обучения в вечерней школе. Пособие для работников вечерней (сменной) школы [Текст] / Г.Д. Глейзер. – М.: 1985. – с. 11.

18. Инусова, Х.М. Модульное обучение - что это такое? [Текст] / Х.М. Инусова // Школьные технологии. – 1998 г. – №2. – с.46-48.

19. Калмыкова, З.И. Темп продвижения как один из показателей индивидуальных различий учащихся [Текст] / З.И. Калмыкова // Вопросы психологии. – 1961 г. – № 2. – с.43.

20. Князева, Е.Н. Синергетика как новое мировидение: диалог с И. Пригожиным [Текст] / Е.Н. Князева, С.П. Курдюмов // Вопросы философии. – 1992 г. – №12. – с.15-22.

21. Куликов, С.И. Принципы модульного обучения [Текст] / С.И. Куликов, Е.М. Дурко // Вестник высшей школы, 1997. – №8. – с.30–33.

22. Куклин, В.Ж. О сравнении педагогических технологий [Текст] / В.Ж. Куклин, В.Г. Наводнов //Высшее образование в России. – 1999. – №1. – с. 165–172.

23. Кукосян, О.Г. Концепция модульной технологии обучения в системе дополнительного профессионального образования: Метод. Пособие [Текст] / О.Г. Кукосян, Г.Н. Князева. – Краснодар, 2001. -29с.

24. Лапчинская, В.П. Средняя образовательная школа современной Англии [Текст] / В.П. Лапчинская. – М., 1977. – 216 с.

25. Левитес, Д.Г. Практика обучения: современные образовательные технологии [Текст] / Д.Г. Левитес. – Мурманск, 1997. – 215с.

26. Левитес, Д.Г. Образовательные технологии: теория, классификация, обзор, конструирование. [Текст] / Д.Г. Левитес. – Мурманск, НИЦ "Пазори", 2001. – 328с.

27. Литвинова, Т.Н. Применение интегративно-модульной системы обучения студентов медицинского вуза общей химии для повышения качества образования [эл.ресурс] // Литвинова Т.Н. – http://www.ksma.ru/fh/juk.k29.doc.

28. Марцинковский, И.Б. Университетское образование в капиталистических странах. [Текст] / И.Б. Марцинковский. – Ташкент, 1981. – 190с.

29. Махмутов, М.И. Педагогические технологии развития мышления учащихся. [Текст] / М.И. Махмутов, Г.И. Ибрагимов, М.А. Чошанов - Казань: ТГЖИ, 1993. – 196с.

30. Никандров, Н.Д. Современная высшая школа капиталистических стран. [Текст] / Н.Д. Никандров. – М., 1978. – 279 с.

31. Пахомова, Е.М. Модульно-рейтинговая система обучения как одна из развивающих технологий обучения [эл.ресурс] // Е.М. Пахомова. – http://www.tgc.ru.

32. Пегушин, В.Л. Педагогика и психология высшей школы. [Текст] / В.Л Пегушин. – Ростов-на-Дону: Феникс, 1998. – 544 с.

33. Пикулин, К.В. Педагогическая технология профессора Монахова [Текст] / К.В. Пикулин // Педагогический вестник: Успешное обучение. – Специальный выпуск. – 1997. – с. 8–15.

34. Пономарева, Л.Н. Обзорный анализ применения модульного обучения в процессе профессиональной подготовки специалистов в вузе [эл.ресурс] / Пономарева Л.Н. – http://science.ncstu.ru/articles/hs/09.

35. Попов, Е.И. Система РИТМ: принципы, организация, методическое содержание [Текст] / Е.И. Попов // Высшее образование в России. – 1998. –№4. – с.109-115.

36. Пуговина, Ю.М. Психология обучения: Учеб. пособие [Текст] / Ю.М. Пуговина / Под ред. В.В. Давыдова. – М., 1978. – с. 25.

37. Роберт, И.В. Современные информационные технологии в образовании; перспективы использования. [Текст] / И.В. Роберт. – М., Школа-Пресс, 1994. – 263с.

38. Родина, В.В. Опыт разработки модульно-блочной системы обучения. [Текст] / В.В. Родина /Сб. трудов. Научно-методич. конф. Ставропольской госсельхоз академии. – Ставрополь, 1995. № 58. – с.28–29.

39. Селевко, Г.К. Современные образовательные технологии. [Текст] / Г.К. Селевко. – М.: Народное образование, 1998. – 271с.

40. Сенновский, И.Б. Система управленческой деятельности учителя в модульной педагогической технологии. [Текст] / И.Б. Сенновский // Школьные технологии. – 1997г. – №2. – с.13.

41. Талызина, Н.Ф. Управление процессом усвоения знаний (психологические основы). [Текст] / Н.Ф. Талызина. – 2-е изд., испр. и доп. М.: 1984. – с.30.

42. Тимофеева, Ю.Ф. Роль модульной системы высшего образования в формировании творческой личности педагога – инженера. [Текст] / Ю.Ф. Тимофеева // Высшее образование в России. – 1993 г. – №4. – с.119.

43. Третьяков, П.И. Технология модульного обучения в школе: Практико-ориентированная монография [Текст] / П.И. Третьяков, И.Б. Сенновский. – М.: Новая школа, 1997. – 352 с.

44. Турышев, В.Н. Модульное обучение в реализации дополнительных профессиональных образовательных программ [Текст] / В.Н. Турышев. – http://www.sgu.ru/dpo/docs/turehev.doc.

45. Халюткин, В.А. Модульно-блочная система обучения [Текст] / В.А. Халюткин // Сб. трудов научно-методич. конф.Ставропольской госсельхоз академии. – Ставрополь, 1995. – №58. – С. 99 – 102.

46. Чошанов, М. Гибкая технология проблемно-модульного обучения. [Текст] / М. Чошанов. – М.: Народное образование, 1996. – 375с.

47. Шамова, Т.И. Основы технологии модульного обучения. [Текст] / Т.И. Шамова // Химия в школе. – 1995г. – №2. – с.14-17.

48. Шамова, Т.И. Модульное обучение: опыт, перспективы [Текст] / Т.И. Шамова. – М.: Изд-во МПГУ им. В.И.Ленина, 1998. – 172с.

49. Юцявичене, П.А. Теория и практика модульного обучения. [Текст] / П.А. Юцявичене. – Каунас, 1989. – 271 с.

50. Якиманская, И.С. Личностно-ориентированное обучение в современной школе. [Текст] / И.С. Якиманская. – М., 1996. – 312с.

51. http://ekrupoderova.narod.ru/osnovy.htm

52. http://city.tomsk.net/~sydney/str_course.html

53. http://him.1september.ru/2003/23/11-1.htm

54. http://74214s013.edusite.ru/p42aa1.html

55. http://www.asu.ru/cppkp/index.files/ucheb.files/innov/Part1/chapter5/5_1_1.html

56. www.ndce.ru/scripts/BookStore/tbcgi.dll/Query?Page=c_card.

57. http://www.library.ru/help/guest.php?PageNum=3213&hv=3214&lv=3205

Школьные учебники:

58. Атанасян, Л.С. Геометрия. Учебник для 10-11 кл. сред. Школы [Текст] / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. – М.: Просвещение, 1994. – 207 с.

59. Погорелов, А.В. Геометрия. Учеб. для 7-11 кл. сред. шк. [Текст] / А.В. Погорелов. – М.: Просвещение,1989. – 303 с.

Приложение 1

Приложение 2

Методика определения уровня обучаемости

6. Учитель выбирает небольшой по объему новый учебный материал базисного характера на 7-8 минут работы.

7. Учитель перед изучением нового повторяет изученный материал, необходимый для усвоения новых знаний.

8. Учитель объясняет новый материал.

9. Учитель показывает образец применения нового материала в аналогичной и измененной ситуациях.

10.Учитель проводит самостоятельную работу среди учащихся.

Задания для самостоятельной работы учащихся

6. Напишите, что вы узнали нового.

7. Ответьте на вопрос по содержанию нового материала.

8. Выполните задания по образцу.

9. Выполните задание в измененной ситуации.

10.Примените полученные знания в новой ситуации.

Ключ к определению уровня обучаемости

Как только 3-4 ученика из класса выполнят задания – собрать рабочие записи у всех. Если выполнены все задания, то можно говорить о третьем, очень высоком уровне обучаемости школьника. Если справился с четырьмя заданиями – второй, также высокий уровень обучаемости. Если выполнены три и менее заданий – первый уровень.

Методика определения уровня обученности

Обученность – это уровень реально усвоенных знаний, умений и навыков. Для ее определения рекомендуют использовать тесты, т.е. проверочные работы, составленные по уровням сложности учебного материала. Опишем уровни обученности.

1. Первый уровень – различение. Характеризует низшую степень обученности. Учащийся только отличает данный учебный элемент от аналогов. Самая низкая ступень овладения знаниями – в дальнейшем возможность только узнавания: ученик может лишь констатировать, что знания были получены раньше, но не может воспроизвести их. На вопросы учителя отвечает односложно, пытаясь угадать правильный ответ.

2. Второй уровень – запоминание. Учащийся может пересказать содержание текста, правила без понимания пересказанного. Может отвечать на вопросы только репродуктивного плана и в соответствии с последовательность изложения материала в учебном пособии.

3. Третий уровень – понимание. Предполагает нахождение существенных признаков и связей предметов и явлений, вычленение их из массива несущественного на основе анализа и синтеза, применение правил логического умозаключения, установление сходства и различия, сопоставление с имеющимися знаниями.

4. Четвертый уровень – простейшие умения и навыки. Характеризуется тем, что умения проявляются как закрепленные способы применения знаний в практической деятельности навыки как умения, доведенные до автоматизма. Учащийся умеет применять на практике полученные теоретические знания, решает задачи с использованием усвоенных законов и правил, вскрывает причинно-следственные связи. Наличие элементарных умений и навыков – показатель довольно высокой степени обученности.

5. Пятый уровень – перенос. Обладающие этой наивысшей степенью обученности умеют обобщать, применять полученные знания в новой ситуации, «переносить» в нее усвоенные ранее понятия и закономерности. Ученик дает ответ на любой вопрос, решает любой пример и задачу по данной теме, находит оригинальные подходы к решению предложенных ему проблемных ситуаций.

Уровни преподавания определяются по итогам уровневых контрольных работ. Степень обученности ученика или степень обученности учащихся (СОУ) рассчитывается по формуле

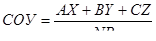где А, B, C – коэффициенты; X, Y, Z - соответственно общее количество отметок «5», «4», «3» в классе или по отдельному предмету; N – количество учащихся в классе; P – число изучаемых предметов.

Коэффициенты	A	B	C
Уровни преподавания: 1-й	1,00	0,64	0,36
2-й	0,64	0,36	0,16
3-й	0,36	0,16	0,04

Пример расчета СОУ.

1. по итогам уровневых контрольных работ получен первый уровень преподавания.

2. В 8 «а» классе у 27 учащихся по 7 предметам: «5» - у 74, «4» - у 86, «3» - у 25, «2» - у 5.

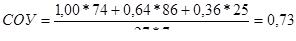, или 73 %.

Степень обученности можно представить графически. Ученика, который достиг высшего показателя, будем считать обученным полностью. Общая обученность складывается из пяти слагаемых, соответствующих пяти уровням обученности (табл.2, рис.1).

Таблица 2

Степень обученности

Показатели	Степень обученности по уровням
Показатели	1-му	2-му	3-му	4-му	5-му
1. Какую часть от общей СОУ составляет данный уровень	1/25	3/25	5/25	7/25	9/25
2. То же, %	4	12	20	28	36
3. Степень обученности учащихся (СОУ) при достижении этого показателя, %	4	16	36	64	100

Рис. 1. Степень обученности:

1 – различение; 2 – запоминание; 3 – понимание; 4 – умения и навыки; 5 – перенос

Известно, что в случае линейной зависимости соотношение последовательных и разнозначных показателей в первом приближении выражается отношением нечетных чисел 1:3:5:7:9. Общая обученность, принятая за 100%, состоит из 1+3+5+7+9=25 частей. Одна часть соответствует 100%:25=4%.

Приложение 3

1. По рисунку 1 определите: А) плоскости, в которых лежат прямые РЕ; Б) плоскости, в которых лежит прямая АВ; 2. По рисунку 2 определите: А) точки, лежащие в плоскостях ДСС₁; Б) точки пересечения прямой ДК с плоскостью АВС; В) точку пересечения прямой МК с плоскостью АДВ; Г) прямые, по которым пересекаются плоскости АА₁В и АСД. Д) прямые, по которым пересекаются плоскости АВ и АВС. 3. Верно ли, что: А) любые три точки лежат в одной плоскости; Б) если а, в и с имеют одну общую точку, то они лежат в одной плоскости. 4. Точки А, В, С и Д не лежат в одной плоскости. Могут ли прямые АВ и СД быть параллельными? Ответ обоснуйте. 5. Верно ли утверждение: если 2 точки окружности принадлежат плоскости, то и вся окружность лежит в этой плоскости? 6. Верно ли, что прямая лежит в плоскости данного треугольника, если она проходит через одну из вершин треугольника?

1. По рисунку 1 определите: А) плоскости, в которых лежат прямые МК; Б) плоскости, в которых лежит прямая В₁С₁; 2. По рисунку 2 определите: А) точки, лежащие в плоскостях BQC; Б) точки пересечения прямой ДР с плоскостью АВС; В) точку пересечения прямой ВР с плоскостью А₁В₁С₁; Г) прямые, по которым пересекаются плоскости ДКС и А₁В₁С₁. Д) прямые, по которым пересекаются плоскости АДС и АВС. 3. Верно ли, что: А) любые 4 точки не лежат в одной плоскости; Б) если прямые а, в и с попарно пересекаются, то они лежат в одной плоскости. 4. Точки А, В, С и Д не лежат в одной плоскости. Могут ли прямые АВ и СД пересекаться)? Ответ обоснуйте. 5. Верно ли утверждение: если три точки окружности принадлежат плоскости, то и вся окружность принадлежит этой плоскости) 6. Верно ли, что прямая лежит в плоскости данного треугольника, если она пересекает две стороны треугольника?

Приложение 4

Приложение 5

Модульное построение учебных занятий (уроков) (по П.И. Третьякову)

* Заполняется конкретно по каждому предмету

Номер Ур.-мод. в теме	Номер УЭ (этапа)	Название этапа	Дидактическая задача	Содержа-ние учебного материала*	Рефлексивная деятельность ученика	Деятельность учителя по обеспечению рефлексии	Показатели реального результата решения задач
1	0	Оргмомент	Подготовка учащихся к работе на занятии		Само- и взаимопроверка	Проверка готовности	Полная готовность класса и оборудования
	1	Подготовка к восприятию. Проверка домашнего задания	Установление правильности и полноты выполнения домашнего задания всеми учащимися		Само-организация и самоосмысление учебного материала	Создание настроя на самоорганизацию (через взаимопроверку)	Оптимальное сочетание контроля, самоконтроля и взаимоконтроля для установления правильности выполнения задания
	2	Мотивация	Обеспечение мотивации и принятия учащимися цели учебно-познавательной деятельности		Самоосмысление (через самопостановку цели)	Создание проблемной ситуации, поискового режима для подготовки к восприятию	Осознанное и быстрое включение учащихся в деловой ритм
	3	Подготовка к основному этапу занятия	Актуализация опорных знаний и умений		Самоосмысление и самоопределение (с решением и конструированием)	Создание ситуации брифинга и подготовки для освоения нового через проблемную модель, задачу	Готовность учащихся к активной учебно-познавательной деятельности на основе опорных знаний
	4	Изучение нового материала	Обеспечение восприятия, осмысления и первичного запоминания знаний и способов действий		Самоосмысление и самоопределение	Изложение материала учителем	Активные действия учащихся с объектом изучения. Максимальное использование самостоятельности в получении знаний
2	1	Первичное закрепление базисного уровня	Установление правильности и осознанности усвоения нового учебного материала		Самоосмысление, самовыражение и самоутверждение	Базисный тест. Определение зоны ближайшего и акту-ального развития. Обучаемость.	Усвоение сущности новых знаний и способов действий на репродуктивном уровне
	2	Коррекция (доводка до базисного уровня)	Выявление пробелов и коррекция		Самоопределение, самовыражение и самоутверждение	Подача материала с учетом зоны ближайшего развития ученика	Ликвидация типичных ошибок и неверных представлений у учащихся
	3	Отработка материала по уроку (систе-матизация, комплексное применение)	Обеспечение усвоения новых знаний и способов действий на уровне применения в измененной ситуации		Самоутверждение, самореализация и саморегуляция (в парах сменного состава)	Использование различных методик КСО	Активная и продуктивная деятельность учащихся по включению части в целое, классификации и систематизации
3	1	Закрепление знаний и умений (уров-невый тест)	Формирование целост-ной системы ведущих знаний по теме, курсу, выделение мировоз-зренческих идей		Самоосмысление, самореализация и саморегуляция	Определение уровня усвоения (обучаемость и обученность)	Самостоятельное выполнение заданий с применением знаний в знакомой и измененной ситуациях
	2	Контроль	Выявление качества и уровня овладения знаниями и способами действий		Самопроверка и взаимопроверка	Экспертный контроль учителя для проведения коррекции	Получение достоверной информации о достижении всеми учащимися планируемых результатов обучения
	3	Коррекция	Коррекция знаний и способов действий		Самокоррекция и взаимокоррекция	Ориентирование на коррекционную работу	Выявление пробелов и неверных представлений и их коррекция
	4	Анализ (подведение итогов урока и оценка)	Анализ и оценка успешности достижения цели. Определение перспективы последующей работы		Самоанализ достигнутого и самооценка	Общий анализ и оценивание	Адекватность самооценки учащегося оценке учителя
	5	Постановка новой цели к следующему уроку	Обеспечение понимания цели домашнего задания		Самоосмысление	Создание мотивации через анализ достигнутого	Получение учащимися информации о реальных результатах учения, задачах на ближайший урок
4	1	Домашнее задание	Обеспечение понимания содержания и способов выполнения домашнего задания		Самовыбор уровня (вида) задания	Дифференци-рованное домашнее задание	Реализация необходимых и достаточных условий для успешного выполнения домашнего задания всеми учащимися в соответствии с актуальным уровнем их развития